atan2

atan2( y , x ) returnerar vinkeln θ mellan strålen till punkten ( x , y ) och den positiva x -axeln, begränsad till (− π , π ] .

Graf över $\operatorname {atan2} (y,x)$ över $y/x$

Inom databehandling och matematik är funktionen atan2 2 - argumentet arctangens . Per definition är $\theta =\operatörsnamn {atan2} (y,x)$ vinkelmåttet ( i radianer , med $-\pi <\theta \leq \pi$ ) mellan den positiva $x$ -axeln och strålen från origo till punkten $(x,\,y)$ i det kartesiska planet . På motsvarande sätt är $\operatorname {atan2} (y,x)$ argumentet (även kallat fas eller vinkel ) för det komplexa talet $x+iy.$

Funktionen $\operatorname {atan2}$ dök upp först i programmeringsspråket Fortran 1961. Den var ursprungligen avsedd att returnera ett korrekt och entydigt värde för vinkeln θ vid konvertering från kartesiska koordinater ( x , y ) till polära koordinater ( r , θ ) . Om $\theta =\operatörsnamn {atan2} (y,x)$ och ${\textstyle r={\sqrt {x^{2}+ y^{2}}}}$ , då $x=r\cos \theta$ och $y=r\sin \theta .$

Om x > 0 är det önskade vinkelmåttet ${\textstyle \theta =\operatörsnamn {atan2} (y,x)=\arctan \left(y/x\right).} Men$ när x < 0 är vinkeln $\ arctan(y/x)$ är diametralt motsatt den önskade vinkeln, och ± π (ett halvt varv ) måste läggas till för att placera punkten i rätt kvadrant . Genom att använda $\operatorname {atan2}$ försvinner denna korrigering, vilket förenklar kod och matematiska formler.

Motivering

Graf över tangentfunktionen från − π till + π med motsvarande tecken för y / x . De gröna pilarna pekar på resultaten av atan2(−1, −1) och atan2(1, 1).

Den vanliga arktangensfunktionen med ett argument returnerar endast vinkelmått i intervallet ${\left[-{\tfrac {1}{2}}\pi ,+{\ tfrac {1}{2}}\pi \right]},$ och när man anropar den för att hitta vinkelmåttet mellan x -axeln och en godtycklig vektor i det kartesiska planet, finns det inget enkelt sätt att ange en riktning i vänster halvplan (det vill säga en punkt $(x,\,y)$ med $x<0$ ). Diametralt motsatta vinkelmått har samma tangent eftersom $y/x=(-y)/(-x),$ så tangenten $y/x$ är i sig inte tillräckligt för att unikt specificera en vinkel.

För att bestämma ett vinkelmått med hjälp av arctangensfunktionen givet en punkt eller vektor $(x,y),$ matematiska formler eller datorkod hantera flera fall; minst en för positiva värden på $x$ och en för negativa värden på $x,$ och ibland ytterligare fall då $y$ är negativ eller en koordinat är noll. Att hitta vinkelmått och omvandla kartesiska till polära koordinater är vanligt inom vetenskaplig beräkning, och denna kod är redundant och felbenägen.

För att råda bot på detta introducerade datorprogrammeringsspråken atan2 -funktionen, åtminstone så tidigt som Fortran IV-språket på 1960-talet. Kvantiteten atan2( y , x ) är vinkelmåttet mellan x -axeln och en stråle från origo till en punkt ( x , y ) var som helst i det kartesiska planet. Tecken på x och y används för att bestämma kvadranten av resultatet och välja rätt gren av flervärdsfunktionen Arctan y / x ) ( .

Funktionen atan2 är användbar i många applikationer som involverar euklidiska vektorer som att hitta riktningen från en punkt till en annan eller konvertera en rotationsmatris till Euler-vinklar .

Atan2 - funktionen ingår nu i många andra programmeringsspråk och är också vanligt förekommande i matematiska formler inom vetenskap och teknik.

Argumentordning

1961 introducerade Fortran funktionen atan2 med argumentordning $(y,x)$ så att argumentet (fasvinkeln) för ett komplext tal är ${\displaystyle \operatörsnamn {arg} z=\operatörsnamn {atan2} (\operatörsnamn {Im} z,\operatörsnamn {Re} z).} Detta följer ordningen från vänster till höger av$ en bråkdel skriven ${ \displaystyle y/x,}$ så att $\operatorname {atan2} (y,x)=\operatörsnamn {atan} (y/x)$ för positiva värden på $x.$ Detta är dock motsatsen till den konventionella komponentordningen för komplexa tal, $z=x+iy,$ eller som koordinater $(\operatörsnamn {Re} z,\operatörsnamn {Im} z).$ Se avsnittet Definition och beräkning .

Vissa andra programmeringsspråk (se § Realiseringar av funktionen i vanliga datorspråk ) valde istället motsatt ordning. Till exempel använder Microsoft Excel $\operatorname {Atan2} (x,y),$ OpenOffice Calc använder $\operatorname {arctan2} (x, y),$ och Mathematica använder $\operatorname {ArcTan} [x,y],$ som standard till en-argument arctangens om anropas med ett argument.

Definition och beräkning

Funktionen atan2 beräknar huvudvärdet för argumentfunktionen som tillämpas på det komplexa talet   x + i y . Det vill säga    atan2( y , x ) = Pr arg( x + i y ) = Arg( x + i y ) . Argumentet skulle kunna ändras med en godtycklig multipel av 2π (motsvarande ett helt varv runt origo) utan att göra någon skillnad på vinkeln, men för att definiera atan2 unikt använder man huvudvärdet i ${\ displaystyle (-\pi ,\pi ]}$ ( , det vill säga − π < atan2( y , x ) ≤ π .

När det gäller standardarctanfunktionen , vars intervall är (−π/2, π/2] , kan det uttryckas på följande sätt för att definiera en yta som inte har några diskontinuiteter förutom längs den halvoändliga linjen x<0 y=0:

$$\operatornamn {atan2} (y,x)={\begin{cases}\arctan \left({\frac {y}{x}}\right)&{\text{if }}x>0,\\[5mu]\arctan \left({\frac {y}{x}}\right )+\pi &{\text{if }}x<0{\text{ och }}y\geq 0,\\[5mu]\arctan \left({\frac {y}{x}}\right) -\pi &{\text{if }}x<0{\text{ och }}y<0,\\[5mu]+{\frac {\pi}{2}}&{\text{if }} x=0{\text{ och }}y>0,\\[5mu]-{\frac {\pi }{2}}&{\text{if }}x=0{\text{ och }}y <0,\\[5mu]{\text{undefined}}&{\text{if }}x=0{\text{ och }}y=0.\end{cases}}$$

Ett kompakt uttryck med fyra överlappande halvplan är

$$\operatörsnamn {atan2} (y,x)={\begin{cases}\arctan \left({\frac {y}{x}} \right)&{\text{if }}x>0,\\[5mu]{\frac {\pi }{2}}-{\arctan }{\bigl (}{\frac {x}{y} }{\bigr )}&{\text{if }}y>0,\\[5mu]-{\frac {\pi }{2}}-{\arctan }{\bigl (}{\frac {x }{y}}{\bigr )}&{\text{if }}y<0,\\[5mu]\arctan \left({\frac {y}{x}}\right)\pm \pi & {\text{if }}x<0,\\[5mu]{\text{undefined}}&{\text{if }}x=0{\text{ och }}y=0.\end{cases} }$$

Iverson -parentesnotationen möjliggör ett ännu mer kompakt uttryck:

$${\begin{aligned}\operatörsnamn {atan2} (y,x)&=\arctan \left({\frac {y}{x}}\right)[x\neq 0]\\[ 5mu]&\qquad +{\bigl (}1-2[y<0]{\bigr )}\left(\pi [x<0]+{\tfrac {1}{2}}\pi [x= 0]\right)\\[5mu]&\qquad +{\text{undefined}}\;\![x=0\wedge y=0]\end{aligned}}$$

Formel utan uppenbar villkorlig konstruktion :

$$\operatörsnamn {atan2} y,x)=\lim _{z\to x^{+}}\arctan \left({\frac {y}{z}}\right)+{\frac {\pi }{2}}\operatörsnamn {sgn}(y)\operatörsnamn {sgn}(x)\left(\operatörsnamn {sgn}(x)-1\right)$$

Följande uttryck härlett från tangenthalvvinkelformeln kan också användas för att definiera atan2 :

$$\ operatornamn {atan2} (y,x)={\begin{cases}2\arctan \left({\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}} \right)&{\text{if }}x>0{\text{ eller }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ och }}y= 0,\\{\text{undefined}}&{\text{if }}x=0{\text{ och }}y=0.\end{cases}}$$

Detta uttryck kan vara mer lämpat för symbolisk användning än definitionen ovan. Den är dock olämplig för allmän flyttalsberäkning , eftersom effekten av avrundningsfel i ${\textstyle {\sqrt {x^{2}+y^{2}}}}$ expanderar nära regionen x < 0, y = 0 (detta kan till och med leda till en division av y med noll).

En variant av den senaste formeln som undviker dessa uppblåsta avrundningsfel:

$$\operatörsnamn {atan2} (y,x)={\begin{cases}2\arctan \left({\frac {y}{{\sqrt { x^{2}+y^{2}}}+x}}\höger)&{\text{if }}x>0,\\2\arctan \left({\frac {{\sqrt {x^ {2}+y^{2}}}-x}{y}}\right)&{\text{if }}x\leq 0{\text{ och }}y\neq 0,\\\pi & {\text{if }}x<0{\text{ och }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ och }}y= 0.\end{cases}}$$

Härledningen av argumentets huvudvärde hänvisar till denna figur

Anmärkningar:

• Detta ger resultat i området (−π, π] .
• Som nämnts ovan kan huvudvärdet för argumentet atan2( y , x ) relateras till arctan( y / x ) genom trigonometri. Härledningen går till så här: Om ( x , y ) = ( r cos θ , r sin θ ) , då tan( θ /2) = y / ( r + x ) . Det följer att
  $$\operatorname {atan2} (y,x)=\theta =2\,\theta /2=2\arctan {\frac {y}{{\sqrt {x^{2}+y^{2} }}+x}}.$$
  Observera att √ x ² + y ² + x ≠ 0 i domänen i fråga.

Derivat

Ytterligare information: Lindningsnummer

Eftersom funktionen atan2 är en funktion av två variabler har den två partiella derivator . Vid punkter där dessa derivator finns atan2 , förutom en konstant, lika med arctan( y / x ) . Därför för x > 0 eller y ≠ 0 ,

${\begin{aligned}&{\frac {\partial }{\partial x}}\operatörsnamn {atan2} (y,\,x)={\frac {\partial }{\partial x}}\ arctan \left({\frac {y}{x}}\right)=-{\frac {y}{x^{2}+y^{2}}},\\[5pt]&{\frac { \partial }{\partial y}}\operatörsnamn {atan2} (y,\,x)={\frac {\partial }{\partial y}}\arctan \left({\frac {y}{x}} \right)={\frac {x}{x^{2}+y^{2}}}.\end{aligned}}$

Gradienten för atan2 ges alltså av

$\nabla {\text{atan2}}(y,x)=\left({-y \över x^{2}+y^{2}},\ {x \över x^{2}+ y^{2}}\höger).$

Att informellt representera funktionen atan2 som vinkelfunktionen θ ( x , y ) = atan2( y , x ) (som bara definieras upp till en konstant) ger följande formel för den totala differentialen :

${\begin{aligned}\mathrm {d} \theta &={\frac {\partial }{\partial x}}\operatörsnamn {atan2} (y,\,x)\,\mathrm {d} x+{\frac {\partial }{\partial y}}\operatörsnamn {atan2} (y,\,x)\,\mathrm {d} y\\[5pt]&=-{\frac {y}{x ^{2}+y^{2}}}\,\mathrm {d} x+{\frac {x}{x^{2}+y^{2}}}\,\mathrm {d} y.\ end{aligned}}$

Medan funktionen atan2 är diskontinuerlig längs den negativa x -axeln, vilket återspeglar det faktum att vinkeln inte kan definieras kontinuerligt, är denna derivata kontinuerligt definierad förutom vid origo, vilket återspeglar det faktum att oändliga (och faktiskt lokala) vinkelförändringar kan definieras överallt förutom ursprunget. Att integrera denna derivata längs en bana ger den totala förändringen i vinkel över banan, och integrering över en sluten slinga ger lindningsnumret .

differentialgeometrins språk är denna derivata en enform , och den är sluten (dess derivata är noll) men inte exakt (den är inte derivatan av en 0-form, dvs. en funktion), och faktiskt genererar den första de Rham-kohomologin för det punkterade planet . Detta är det mest grundläggande exemplet på en sådan form, och det är grundläggande i differentialgeometri.

De partiella derivatorna av atan2 innehåller inte trigonometriska funktioner, vilket gör det särskilt användbart i många applikationer (t.ex. inbäddade system) där trigonometriska funktioner kan vara dyra att utvärdera.

Illustrationer

atan2 för utvalda strålar

Denna figur visar värden på atan2 längs utvalda strålar från ursprunget, märkta vid enhetscirkeln. Värdena, i radianer, visas inuti cirkeln. Diagrammet använder den matematiska standardkonventionen att vinklar ökar moturs från noll längs strålen till höger. Observera att ordningen på argumenten är omvänd; funktionen atan2( y , x ) beräknar vinkeln som motsvarar punkten ( x , y ) .

Jämförelse av arctan och atan2 funktioner

Den här figuren visar värdena för $\arctan(\tan(\theta ))$ tillsammans med $\ operatornamn {atan2} (\sin(\theta ),\cos(\theta ))$ för $0\leq \theta \leq 2\pi$ . Båda funktionerna är udda och periodiska med perioderna $\pi$ respektive ${\displaystyle 2\pi } ,$ och kan således enkelt kompletteras till valfri region med reella värden på $\theta$ . Man kan tydligt se grensnitten för $\operatorname {atan2}$ -funktionen vid $\theta =\pi$ , och för $\arctan$ -funktionen vid $\theta \in \{{\tfrac {\pi }{2}},\;{\tfrac {3\pi }{2}}\}$ .

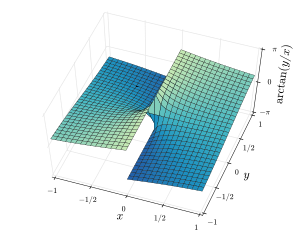
De två figurerna nedan visar 3D-vyer av atan2( y , x ) respektive arctan( y / x ) över ett område av planet. Observera att för atan2( y , x ) har strålar i X / Y -planet som utgår från origo konstanta värden, men för arctan( y / x ) har linjer i X / Y -planet som passerar genom origo konstanta värden. För x > 0 ger de två diagrammen identiska värden.

Vinkelsumma och skillnadsidentitet

Huvudartikel: Lista över trigonometriska identiteter § Vinkelsumma och skillnadsidentiteter

Summor av $\operatorname {atan2}$ kan komprimeras till en enda operation enligt följande identitet

${\displaystylean 2 operatörsnamn {at } (y_{1},x_{1})\pm \operatörsnamn {atan2} (y_{2},x_{2})=\operatörsnamn {atan2} (y_{1}x_{2}\pm y_{2 }x_{1},x_{1}x_{2}\mp y_{1}y_{2})}$

...förutsatt att $\operatorname {atan2} (y_{1},x_{1}) \pm \operatörsnamn {atan2} (y_{2},x_{2})\in (-\pi ,\pi ]$ .

Beviset innebär att man överväger två fall, ett där $y_{2}\neq 0$ eller $x_{2}>0$ och ett där $y_{2} =0$ och $x_{2}<0$ .

Vi tar bara hänsyn till fallet där $y_{2}\neq 0$ eller $x_{2}>0$ . Till att börja med gör vi följande observationer:

1. $-\operatörsnamn {atan2} (y,x)=\operatörsnamn {atan2} (-y,x)$ förutsatt att ${\ displaystyle y\neq 0}$ eller $x>0$ .
2. ${\displaystyle \operatorname {Arg} (x+iy)=\operatörsnamn {atan2} (y,x)} ,$ där $\operatorname { Arg}$ är den komplexa argumentfunktionen .
3. $\theta =\operatörsnamn {Arg} e^{i\theta }$ närhelst $\theta \in (-\pi ,\pi ]$ , en konsekvens av Eulers formel .
4. $\operatorname {Arg} (e^{i\operatörsnamn {Arg} \zeta _{1}} e^{i\operatörsnamn {Arg} \zeta _{2}})=\operatörsnamn {Arg} (\zeta _{1}\zeta _{2})$ .

För att se (4) har vi identiteten $e^{i\operatörsnamn {Arg} \zeta }={\bar {\zeta }}$ där ${\bar {\zeta }}=\zeta /\left|\zeta \right|$ , därav $\operatörsnamn {Arg} (e^{i\operatörsnamn {Arg} \zeta _{1}}e^{i\operatörsnamn {Arg} \zeta _{2}})=\operatörsnamn {Arg } ({\bar {\zeta _{1}}}{\bar {\zeta _{2}}})$ . Dessutom, eftersom $\operatorname {Arg} \zeta =\operatorname {Arg} a\zeta$ för varje positivt reellt värde $a$ , så om vi låter $\zeta =\zeta _{1}\zeta _{2}$ och ${\displaystyle a={\frac {1}{\left|\zeta _{1}\right|\left|\zeta _{2}\right|}}} då har$ vi $\operatorname {Arg} ({\bar {\zeta _{1}}}{\bar {\zeta _{2}}})=\operatörsnamn {Arg } (\zeta _{1}\zeta _{2})$ .

Från dessa observationer har följande ekvivalenser:

${\begin{aligned}\operatörsnamn {atan2} (y_{1},x_{1})\pm \operatörsnamn {atan2} (y_{2},x_ {2})&{}=\operatörsnamn {atan2} (y_{1},x_{1})+\operatörsnamn {atan2} (\pm y_{2},x_{2})&{\text{av ( 1)}}\\&{}=\operatörsnamn {Arg} (x_{1}+iy_{1})+\operatörsnamn {Arg} (x_{2}\pm iy_{2})&{\text{av (2)}}\\&{}=\operatörsnamn {Arg} e^{i(\operatörsnamn {Arg} (x_{1}+iy_{1})+\operatörsnamn {Arg} (x_{2}\pm iy_{2}))}&{\text{av (3)}}\\&{}=\operatörsnamn {Arg} (e^{i\operatörsnamn {Arg} (x_{1}+iy_{1}) }e^{i\operatörsnamn {Arg} (x_{2}\pm iy_{2})})\\&{}=\operatörsnamn {Arg} ((x_{1}+iy_{1})(x_{ 2}\pm iy_{2}))&{\text{av (4)}}\\&{}=\operatörsnamn {Arg} (x_{1}x_{2}\mp y_{1}y_{2 }+i(y_{1}x_{2}\pm y_{2}x_{1}))\\&{}=\operatörsnamn {atan2} (y_{1}x_{2}\pm y_{2} x_{1},x_{1}x_{2}\mp y_{1}y_{2})&{\text{by (2)}}\end{aligned}}$

Följd : om $(y_{1},x_{1})$ och $(y_{2},x_{2})$ är 2 -dimensionella vektorer, används skillnadsformeln ofta i praktiken för att beräkna vinkeln mellan dessa vektorer med hjälp av $\operatorname {atan2}$ , eftersom den resulterande beräkningen beter sig godartat i området ${ \displaystyle (-\pi ,\pi ]}$ och kan alltså användas utan intervallkontroller i många praktiska situationer.

Öst-moturs, nord-urs och söder-urs konventioner, etc.

Funktionen $\displaystyle \mathrm {atan2} }$ designades ursprungligen för konventionen i ren matematik som kan kallas öst-motsols . I praktiska tillämpningar är dock nord- och syd-urs ofta normen. Inom atmosfärsvetenskap, till exempel, vindriktningen beräknas med hjälp av funktionen $\mathrm {atan2}$ med vindvektorns öst- och nordkomponenter som argument; solens azimutvinkel kan beräknas på liknande sätt med öst- och nordkomponenterna av solvektorn som argument. Vindriktningen definieras normalt i nord-urs riktning, och solens azimutvinkel använder både nord-medurs och syd-urs konventioner i stor utsträckning. Dessa olika konventioner kan realiseras genom att byta positioner och ändra tecknen för x- och y-argumenten enligt följande:

• $\mathrm {atan2} (y,x),\;\;\;\;\;$ (öst-moturs konvention)
• $\mathrm {atan2} (x,y),\;\;\;\;\;$ (Nord-medsols konvention)
• $\mathrm {atan2} (-x,-y)$ . (Syd-medurs konvention)

Som ett exempel, låt $x_{0}={\frac {\sqrt {3}}{2}}$ och $y_{0}={\frac {1 }{2}}$ , då ger formatet öst-motsols $\mathrm {atan2} (y_{0},x_{0})\ cdot {\frac {180}{\pi }}=30^{\circ }$ , formatet nord medurs ger $\mathrm {atan2 } (x_{0},y_{0})\cdot {\frac {180}{\pi }}=60^{\circ }$ och formatet söder medurs ger $\mathrm {atan2} (-x_{0},-y_{0})\cdot {\frac {180}{\pi }}=-120^{\ circ }$ .

Tydligen kan att ändra tecknet för x- och/eller y-argumenten och byta deras positioner skapa 8 möjliga varianter av funktionen $\displaystyle \mathrm {atan2} }$ och de motsvarar, intressant nog, 8 möjliga definitioner av vinkeln, nämligen medurs eller moturs med början från var och en av de fyra kardinalriktningarna , norr, öster, syd och väster.

Realiseringar av funktionen i vanliga datorspråk

Förverkligandet av funktionen skiljer sig från ett datorspråk till ett annat:

• I Microsoft Excel , OpenOffice.org Calc , LibreOffice Calc , Google Spreadsheets , iWork Numbers och ANSI SQL:2008 standarden har arctangensfunktionen med 2 argument de två argumenten i standardsekvensen $(\operatorname {Re} ,\operatorname {Im} )$ (omvänt i förhållande till konventionen som används i diskussionen ovan).
• I Mathematica används formen ArcTan[ x , y ] där en parameterform tillhandahåller den normala arctangensen. Mathematica klassificerar ArcTan[0, 0] som ett obestämt uttryck.
• På de flesta grafräknare för TI (exklusive TI-85 och TI-86 ) kallas motsvarande funktion R►Pθ och har argumenten $(\operatörsnamn {Re} ,\operatörsnamn {Im} )$ .
• På TI-85 kallas arg -funktionen angle(x,y) och även om den verkar ta två argument, har den egentligen bara ett komplext argument som betecknas med ett par tal:   x + i y = ( x , y ) .

${\displaystyle (\operatorname {Im} ,\operatorname {Re} )}-$ konventionen används av:

• C-funktionen atan2 , och de flesta andra datorimplementationer, är designade för att minska ansträngningen att transformera kartesiska till polära koordinater och definierar därför alltid atan2(0, 0) . På implementeringar utan tecken på noll , eller när de ges positiva nollargument, definieras det normalt som 0. Det kommer alltid att returnera ett värde i intervallet [−π, π] istället för att höja ett fel eller returnera ett NaN (Inte ett tal).
• I Common Lisp , där valfria argument finns, tillåter atan -funktionen en valfritt att ange x -koordinaten:   (atan y x ) .
• I Julia liknar situationen Common Lisp: istället för atan2 har språket en enparameter och en tvåparameterform för atan . Den har dock många fler än två metoder för att möjliggöra aggressiv optimering vid kompilering (se avsnittet "Varför kompilerar du inte Matlab/Python/R/...-kod till Julia?" ).
• För system som implementerar tecken noll , oändligheter eller inte ett tal (till exempel IEEE flyttal ), är det vanligt att implementera rimliga tillägg som kan utöka intervallet av värden som produceras till att inkludera − π och −0 när y = −0. Dessa kan också returnera NaN eller ta upp ett undantag när de ges ett NaN-argument.
• I Intel x86 Architecture assembler-koden är atan2 känd som FPATAN- instruktionen ( floating -point partial arctangent). Den kan hantera oändligheter och resultaten ligger i det slutna intervallet [−π, π] , t.ex. atan2(∞, x ) = + π /2 för finita x . Speciellt definieras FPATAN när båda argumenten är noll:

  atan2(+0, +0) = +0;

  atan2(+0, −0) = + π ;

  atan2(−0, +0) = −0;

  atan2(−0, −0) = − π .

Denna definition är relaterad till begreppet tecken noll .

• I andra matematiska skrifter än källkod, såsom i böcker och artiklar, har beteckningarna Arctan och Tan ⁻¹ använts; dessa är varianter med versaler av den vanliga arctan och tan ⁻¹ . Denna användning överensstämmer med den komplexa argumentnotationen , så att   Atan( y , x ) = Arg( x + i y ) .
• På HP- kalkylatorer behandlar du koordinaterna som ett komplext tal och tar sedan ARG . Eller << C->R ARG >> 'ATAN2' STO .
• På vetenskapliga miniräknare kan funktionen ofta beräknas som den vinkel som ges när ( x , y ) omvandlas från rektangulära koordinater till polära koordinater .
• System som stöder symbolisk matematik returnerar normalt ett odefinierat värde för atan2(0, 0) eller signalerar på annat sätt att ett onormalt tillstånd har uppstått.
• Det kostnadsfria matematikbiblioteket FDLIBM (Freely Distributable LIBM) tillgängligt från netlib har källkod som visar hur det implementerar atan2 inklusive hantering av de olika IEEE-exceptionella värdena.
• För system utan hårdvarumultiplikator kan funktionen atan2 implementeras på ett numeriskt tillförlitligt sätt med CORDIC -metoden. Således kommer implementeringar av atan( y ) förmodligen att välja att beräkna atan2( y , 1) .

Se även

• hypot

externa länkar

• ATAN2 Online-kalkylator
• Java 1.6 SE JavaDoc
• atan2 vid Allt2
• PicBasic Pro-lösning atan2 för en PIC18F

Andra implementeringar/kod för atan2

• "Bäring mellan två punkter" . Arkiverad från originalet den 18 november 2020 . Hämtad 21 februari 2022 .

• "Arctan och polära koordinater" . Arkiverad från originalet den 18 oktober 2018 . Hämtad 21 februari 2022 .

• "Vad är 'Arccos'?" . Arkiverad från originalet den 6 september 2017 . Hämtad 21 februari 2022 .