Van Deemters ekvation

Van Deemter-ekvationen i kromatografi , uppkallad efter Jan van Deemter , relaterar variansen per längdenhet för en separationskolonn till den linjära mobila fasens hastighet genom att beakta fysiska, kinetiska och termodynamiska egenskaper hos en separation. Dessa egenskaper inkluderar vägar inom kolonnen, diffusion ( axiell och longitudinell) och massöverföringskinetik mellan stationära och mobila faser. Vid vätskekromatografi tas den mobila fasens hastighet som utgångshastigheten, det vill säga förhållandet mellan flödeshastigheten i ml/sekund och tvärsnittsarean av "kolonn-utgångsflödesbanan". För en packad kolonn är tvärsnittsarean för kolonnens utloppsflödesväg vanligtvis tagen till 0,6 gånger kolonnens tvärsnittsarea. Alternativt kan den linjära hastigheten tas som förhållandet mellan kolumnlängden och dödtiden. Om den mobila fasen är en gas tryckkorrigeringen tillämpas. Variansen per längdenhet av kolonnen tas som förhållandet mellan kolonnens längd och kolonnens effektivitet i teoretiska plattor . Van Deemter-ekvationen är en hyperbolisk funktion som förutsäger att det finns en optimal hastighet vid vilken det kommer att finnas den minsta variansen per kolumnlängdsenhet och därmed en maximal effektivitet. Van Deemter-ekvationen var resultatet av den första tillämpningen av hastighetsteori på kromatografi-elueringsprocessen.

Van Deemters ekvation

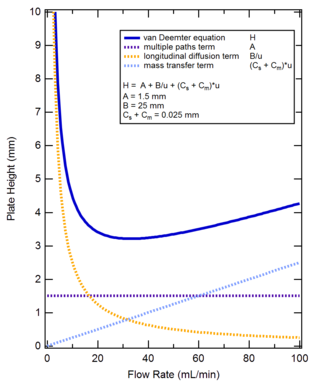
Van Deemter-ekvationen relaterar höjd som motsvarar en teoretisk platta (HETP) i en kromatografisk kolonn till de olika flödes- och kinetiska parametrarna som orsakar toppbreddning, enligt följande:

$HETP=A+{\frac {B}{u}}+(C_{s}+C_{m})\cdot u$

Var

• HETP = ett mått på kolonnens upplösningsförmåga [m]
• A = Eddy-diffusion parameter, relaterad till kanalisering genom en icke-ideal packning [m]
• B = diffusionskoefficient för de eluerande partiklarna i längdriktningen, vilket resulterar i dispersion [m ² s ^{−1 ]}
• C = Resistens mot massöverföringskoefficient för analyten mellan mobil och stationär fas [s]
• u = hastighet [ms ⁻¹ ]

I öppna rörformiga kapillärer kommer A-termen att vara noll eftersom avsaknaden av packning betyder att kanalisering inte inträffar. I packade kolonner existerar emellertid flera distinkta vägar ("kanaler") genom kolumnpackningen, vilket resulterar i bandspridning. I det senare fallet kommer A inte att vara noll.

Formen på Van Deemter-ekvationen är sådan att HETP uppnår ett minimivärde vid en viss flödeshastighet. Vid denna flödeshastighet är kolonnens upplösningsförmåga maximerad, även om elueringstiden i praktiken sannolikt är opraktisk. Att differentiera van Deemter-ekvationen med avseende på hastighet, sätta det resulterande uttrycket lika med noll och lösa för den optimala hastigheten ger följande:

$u={\sqrt {\frac {B}{C}}}$

Antal tallrikar

Två väl upplösta toppar i ett kromatogram

Platthöjden ges som:

$H={\frac {L}{N}}\,$

med $L\,$ kolumnlängden och $N\,$ kan antalet teoretiska plattor uppskattas från ett kromatogram genom analys av retentionstiden $t_{R}\,$ för varje komponent och dess standardavvikelse $\sigma \,$ som ett mått på toppbredd, förutsatt att elueringskurvan representerar en Gauss-kurva .

I det här fallet ges plåtantalet av:

$N=\left({\frac {t_{R}}{\sigma }}\right)^{2}\,$

Genom att använda den mer praktiska toppbredden vid halv höjd $W_{1/2}\,$ är ekvationen:

$N=8\ln(2)\cdot \left({\frac {t_{R}}{W_{1/2} }}\right)^{2}\,$

eller med bredden vid toppen av toppen:

$N=16\cdot \left({\frac {t_{R}}{W_{base}}}\right)^{2}\,$

Utökad van Deemter

Van Deemter-ekvationen kan utökas ytterligare till:

$H=2\lambda d_{p}+{2\gamma D_{m} \over u}+{\omega (d_{p}{\mbox{ eller }}d_{c})^{2}u \over D_{m}}+{Rd_{f}^{2 }u \över D_{s}}$

Var:

• H är plattans höjd
• λ är partikelform (med hänsyn till packningen)
• dp _är partikeldiameter
• γ, ω och R är konstanter
• D _m är diffusionskoefficienten för den mobila fasen
• d _c är kapillärdiametern
• d _f är filmtjockleken
• D _s är diffusionskoefficienten för den stationära fasen.
• u är den linjära hastigheten

Rodrigues ekvation

Rodrigues ekvation , uppkallad efter Alírio Rodrigues , är en förlängning av Van Deemter-ekvationen som används för att beskriva effektiviteten hos en bädd av permeabla (storporiga) partiklar.

Ekvationen är:

$HETP=A+{\frac {B}{u}}+C\cdot f(\lambda )\cdot u$

var

$f(\lambda )={\frac {3}{\lambda }}\left[{\frac {1}{\tanh (\lambda )}}-{\frac {1}{\lambda }}\right]$

och $\lambda$ är det intrapartikulära Péclet-talet .

Se även

• Upplösning (kromatografi)
• Jan van Deemter