Ung–Laplace ekvation

Ej att förväxla med Youngs ekvation för ytvätning eller Laplaces ekvation .

Inom fysiken är Young –Laplace-ekvationen ( / statiska som upprätthålls ləˈpl ɑːs , , / ) en algebraisk ekvation som beskriver den kapillära tryckskillnaden över gränsytan mellan två vätskor såsom vatten och luft på grund av fenomenet yta spänning eller väggspänning , även om användning av den senare endast är tillämplig om man antar att väggen är mycket tunn. Young–Laplace-ekvationen relaterar tryckskillnaden till formen på ytan eller väggen och den är fundamentalt viktig i studiet av statiska kapillärytor . Det är ett uttalande om normal spänningsbalans för statiska vätskor som möts vid ett gränssnitt, där gränssnittet behandlas som en yta (noll tjocklek):

$${\begin{aligned}\Delta p&=-\gamma \nabla \cdot {\hat {n}}\\&=-2\gamma H_{f}\\&=-\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2 }}}\right)\end{aligned}}$$

där $\Delta p$ är Laplace-trycket , tryckskillnaden över vätskegränsytan (det yttre trycket minus det inre trycket), $\gamma$ är ytspänningen (eller väggspänningen ), ${\hat {n}}$ är den normala enheten som pekar ut från ytan, $H_{f}$ är medelkurvaturen och $R_{1}$ och $R_{2}$ är de huvudsakliga krökningsradierna . Observera att endast normal spänning beaktas, detta beror på att det har visat sig att ett statiskt gränssnitt är möjligt endast i frånvaro av tangentiell spänning.

Ekvationen är uppkallad efter Thomas Young , som utvecklade den kvalitativa teorin om ytspänning 1805, och Pierre-Simon Laplace som avslutade den matematiska beskrivningen året därpå. Det kallas ibland också Young–Laplace–Gauss-ekvationen, eftersom Carl Friedrich Gauss förenade Youngs och Laplaces arbete 1830, och härledde både differentialekvationen och gränsvillkoren med hjälp av Johann Bernoullis virtuella arbetsprinciper .

Tvålfilmer

Huvudartikel: Tvålfilm

Om tryckskillnaden är noll, som i en tvålfilm utan gravitation, kommer gränsytan att anta formen av en minimal yta .

Emulsioner

Ekvationen förklarar också den energi som krävs för att skapa en emulsion . För att bilda de små, mycket krökta dropparna i en emulsion krävs extra energi för att övervinna det stora trycket som blir resultatet av deras lilla radie.

Laplace-trycket, som är högre för mindre droppar, orsakar diffusion av molekyler ur de minsta dropparna i en emulsion och driver emulsionens förgrovning via Ostwald-mognad .

Kapillärtryck i ett rör

Sfärisk menisk med vätningsvinkel mindre än 90°

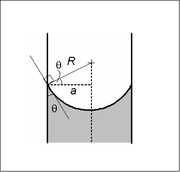
I ett tillräckligt smalt (dvs lågt bindningstal ) rör med cirkulärt tvärsnitt (radie a ) bildar gränsytan mellan två vätskor en menisk som är en del av ytan på en sfär med radien R . Tryckhoppet över denna yta är relaterat till radien och ytspänningen γ by

$$\Delta p={\frac {2\gamma }{R}}.$$

Detta kan visas genom att skriva Young–Laplace-ekvationen i sfärisk form med ett kontaktvinkelgränsvillkor och även ett föreskrivet höjdgränsvillkor vid till exempel botten av menisken. Lösningen är en del av en sfär, och lösningen kommer endast att finnas för tryckskillnaden som visas ovan. Detta är signifikant eftersom det inte finns någon annan ekvation eller lag för att specificera tryckskillnaden; förekomsten av lösning för ett specifikt värde av tryckskillnaden föreskriver det.

Sfärens radie kommer endast att vara en funktion av kontaktvinkeln θ , som i sin tur beror på de exakta egenskaperna hos vätskorna och behållarmaterialet som vätskorna i fråga kommer i kontakt med/gränssnitt med:

$$R={\frac {a}{\cos \theta }}$$

så att tryckskillnaden kan skrivas som:

$$\Delta p={\frac {2\gamma \cos \theta }{a}}.$$

Illustration av kapillärstigning. Röd=kontaktvinkel mindre än 90°; blå=kontaktvinkel större än 90°

För att upprätthålla hydrostatisk jämvikt balanseras det inducerade kapillärtrycket av en förändring i höjden, h , som kan vara positiv eller negativ, beroende på om vätningsvinkeln är mindre än eller större än 90°. För en vätska med densitet ρ:

$$\rho gh={\frac {2\gamma \cos \theta }{a}}.$$

där g är gravitationsaccelerationen . Detta är ibland känt som Jurins lag eller Jurinhöjd efter James Jurin som studerade effekten 1718.

För ett vattenfyllt glasrör i luft vid havsnivå :

• y = 0,0728 J/m2 ^vid 20° C
• θ = 20° (0,35 rad )
• ρ = 1000 kg/m ³
• g = 9,8 m/s ²

och så höjden på vattenpelaren ges av:

$$h\approx {{1,4\times 10^{-5}}\mathrm {m} \over a}.$$

För ett 2 mm brett (1 mm radie) rör skulle vattnet alltså stiga 14 mm. Men för ett kapillärrör med en radie på 0,1 mm skulle vattnet stiga 14 cm (cirka 6 tum ).

Kapillärverkan i allmänhet

I det allmänna fallet, för en fri yta och där det finns ett applicerat "övertryck", Ap, vid gränsytan i jämvikt, finns det en balans mellan det applicerade trycket, det hydrostatiska trycket och effekterna av ytspänning. Young –Laplace ekvationen blir:

$$\Delta p=\rho gh-\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)$$

Ekvationen kan vara icke-dimensionaliserad i termer av dess karakteristiska längdskala, kapillärlängden :

$$L_{c}={\sqrt {\frac {\gamma }{\rho g}}},$$

och karakteristiskt tryck

$$p_{c}={\frac {\gamma }{L_{c}}}={\sqrt {\gamma \rho g}}.$$

För rent vatten med standardtemperatur och standardtryck är kapillärlängden ~ 2 mm .

Den icke-dimensionella ekvationen blir då:

$$h^{*}-\Delta p^{*}=\left({\frac {1}{{R_{1}}^{*}}}+{\frac {1}{{R_{ 2}}^{*}}}\höger).$$

Således bestäms ytformen av endast en parameter, vätskans övertryck, Δ p ^* och ytans skala ges av kapillärlängden . Lösningen av ekvationen kräver ett initialt villkor för position, och ytans gradient vid startpunkten.

₀₀ Ett hängande fall produceras för ett övertryck på Δp ^* =3 och initialtillstånd r =10 ⁻⁴ , z =0, dz / dr =0

₀₀ En vätskebrygga produceras för ett övertryck på Δp ^* =3,5 och initialtillstånd r =0,25 ⁻⁴ , z =0, dz / dr =0

Axisymmetriska ekvationer

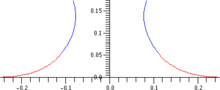
Den (icke-dimensionella) formen, r ( z ) av en axisymmetrisk yta kan hittas genom att ersätta allmänna uttryck för huvudsakliga krökningar för att ge de hydrostatiska Young–Laplace-ekvationerna :

$${\frac {r''}{(1+r'^{2} )^{{3}/{2}}}}-{\frac {1}{r(z){\sqrt {1+r'^{2}}}}}=z-\Delta p^{* }$$

$${\frac {z''}{(1+z'^{2})^{3/2}}}+{\frac {z'}{r(1+z'^{2}) ^{{1}/{2}}}}=\Delta p^{*}-z(r).$$

Tillämpning inom medicin

I medicin ses det ofta till som Laplace-lagen , som används i kontexten av kardiovaskulär fysiologi och även andningsfysiologi , även om den senare användningen ofta är felaktig.

Historia

Francis Hauksbee utförde några av de tidigaste observationerna och experimenten 1709 och dessa upprepades 1718 av James Jurin som observerade att vätskans höjd i en kapillärpelare endast var en funktion av tvärsnittsarean vid ytan, inte av någon annan. kolonnens dimensioner.

Thomas Young lade grunden till ekvationen i sin uppsats från 1804 An Essay on the Cohesion of Fluids där han i beskrivande termer beskrev principerna för kontakt mellan vätskor (tillsammans med många andra aspekter av vätskebeteende). Pierre Simon Laplace följde upp detta i Mécanique Céleste med den formella matematiska beskrivningen ovan, som i symboliska termer återgav förhållandet som Young beskrev tidigare.

Laplace accepterade idén från Hauksbee i sin bok Physico-mechanical Experiments (1709), att fenomenet berodde på en attraktionskraft som var okänslig på vettiga avstånd. Den del som handlar om verkan av ett fast ämne på en vätska och den ömsesidiga verkan av två vätskor utarbetades inte noggrant, utan slutfördes slutligen av Carl Friedrich Gauss . Franz Ernst Neumann (1798-1895) fyllde senare i några detaljer.

Vidare läsning

• Maxwell, James Clerk ; Strutt, John William (1911). "Kapillärverkan" . I Chisholm, Hugh (red.). Encyclopædia Britannica . Vol. 5 (11:e upplagan). Cambridge University Press. s. 256–275.
• Batchelor, GK (1967) An Introduction To Fluid Dynamics , Cambridge University Press
•   Jurin, J. (1716). "En redogörelse för några experiment visade inför Royal Society; med en undersökning av orsaken till uppstigningen och suspensionen av vatten i kapillärrör" . Philosophical Transactions of the Royal Society . 30 (351–363): 739–747. doi : 10.1098/rstl.1717.0026 . S2CID 186211806 .
• Tadros TF (1995) Surfactants in Agrochemicals , Surfactant Science series, vol. 54, Dekker