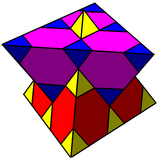
Trigonal trapezoedrisk bikaka
| Trigonal trapezoedrisk bikaka | |
|---|---|
| (ingen bild) | |
| Typ | Dubbel enhetlig honungskaka |
| Coxeter-Dynkin diagram |
|
| Cell |
 Trigonal trapezoeder (1/4 av rombisk dodekaeder ) |
| Ansikten | Romb |
| Rymdgrupp | Fd 3 m (227) |
| Coxeter grupp | ×2, 3 [4] (dubbel) |
| vertexfigurer |
|
| Dubbel | Kvartskubisk honungskaka |
| Egenskaper | Cell-transitive , Face-transitive |
I geometri är den trigonala trapezoedriska bikakan en enhetlig rymdfyllande tessellation (eller honeycomb ) i Euklidiskt 3-utrymme . Celler är identiska trigonala trapets eller romboedrar . Conway, Burgiel och Goodman-Strauss kallar det en oblate cubille .
Relaterade vaxkakor och plattsättningar
Denna bikakekaka kan ses som en rombisk dodekaedrisk honungskaka , med de rombiska dodekaedrarna dissekerade med sitt centrum i 4 trigonala trapets eller romboedrar .
 rombisk dodekaedrisk honungskaka |
 Rombisk dodekaedrisk dissektion |
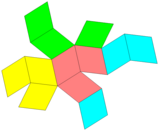 Rombiskt nät |
Det är analogt med att den vanliga hexagonalen är dissekerbar i 3 rombier och belägger planet som en romb . Rombeklädnaden är faktiskt en ortogonal projektion av den trigonala trapetsoedriska bikakan . En annan ortogonal projektion producerar kvadrillen där romberna förvrängs till kvadrater.

|

|
Dubbel plattsättning
Den är dubbel till den kvartskubiska bikakan med tetraedriska och trunkerade tetraedriska celler: