Transversalitet (matematik)

Inom matematiken är transversalitet en föreställning som beskriver hur utrymmen kan skära varandra ; transversalitet kan ses som "motsatsen" till tangency , och spelar en roll i allmän position . Det formaliserar idén om en generisk skärningspunkt i differentiell topologi . Den definieras genom att beakta linjäriseringarna av de skärande utrymmena vid skärningspunkterna.

Definition

Tvärgående kurvor på ytan av en sfär

Icke-tvärgående kurvor på ytan av en sfär

Två undergrenrör av ett givet ändligt dimensionellt jämnt grenrör sägs skära tvärs om vid varje skärningspunkt, deras separata tangentutrymmen vid den punkten tillsammans genererar tangentutrymmet för det omgivande grenröret vid den punkten. Förgreningsrör som inte skär varandra är vacuously tvärgående. Om grenrören är av komplementär dimension (dvs. deras dimensioner summerar till dimensionen för det omgivande utrymmet ), innebär villkoret att tangentutrymmet till det omgivande grenröret är den direkta summan av de två mindre tangentutrymmena. Om en korsning är tvärgående, kommer skärningen att vara en undergren vars kodimension är lika med summan av de två grenrörens samdimensioner. I frånvaro av transversalitetsvillkoret kan skärningspunkten misslyckas med att vara en undergren, med någon sorts singulär punkt .

I synnerhet betyder detta att tvärgående undergrenrör av komplementär dimension skär varandra i isolerade punkter (dvs. ett 0-grenrör ) . Om båda undergrenrören och det omgivande grenröret är orienterade , är deras skärningspunkt orienterad. När skärningspunkten är nolldimensionell är orienteringen helt enkelt ett plus eller minus för varje punkt.

En notation för den tvärgående skärningspunkten mellan två undergrenrör $L_{1}$ och $L_{2}$ för ett givet grenrör $M$ är $L_ {1}\pitchfork L_{2}$ . Denna notation kan läsas på två sätt: antingen som " $L_{1}$ och $L_{2}$ skär tvärs över" eller som en alternativ notation för den mängdteoretiska skärningspunkten $L_{1}\cap L_{2}$ av $L_{1}$ och $L_{2}$ när den skärningen är tvärgående. I denna notation lyder definitionen av transversalitet

L_{1}\pitchfork L_{2}\iff \forall p\in L_{1}\cap L_{2},T_{p}M=T_{p}L_{1}+T_{p} L_{2}.

Transversalitet av kartor

Begreppet transversalitet för ett par undergrenrör utvidgas lätt till transversalitet av ett undergrenrör och en karta till omgivande grenrör, eller till ett par kartor till omgivande grenrör, genom att fråga om framskjutningen av tangentutrymmena längs förbilden av punkter av skärningspunkten mellan bilderna genererar hela tangentutrymmet i det omgivande grenröret. Om kartorna är inbäddningar är detta ekvivalent med transversalitet av undergrenar.

Betydelse av transversalitet för olika dimensioner

Transversalitet beror på omgivande utrymme. De två kurvorna som visas är tvärgående när de betraktas som inbäddade i planet, men inte om vi betraktar dem som inbäddade i ett plan i tredimensionellt utrymme

Antag att vi har tvärgående kartor $f_{1}:L_{1}\to M$ och $f_{2}:L_{2}\to M$ där $L_{1},L_{2}}$ $\ell _{1},\ell _ {2}$ och $M$ är grenrör med dimensionerna respektive $m$ .

Betydelsen av transversalitet skiljer sig mycket beroende på de relativa dimensionerna av $M,L_{1}$ och $L_{2}$ . Relationen mellan transversalitet och tangens är tydligast när $\ell _{1}+\ell _{2}=m$ .

Vi kan överväga tre separata fall:

När $\ell _{1}+\ell _{2}<m$ är det omöjligt för bilden av $L_{1}$ och ${\ displaystyle L_{2}}$ s tangentrymden för att spänna över $M$ s tangentrymd vid vilken punkt som helst. Således kan varje skärning mellan $f_{1}$ och $f_{2}$ inte vara tvärgående. Emellertid uppfyller icke-korsande grenrör vakuum villkoret, så kan sägas skära tvärs.
När $\ell _{1}+\ell _{2}=m$ , bilden av $L_{1}$ och $L_{2 }$ s tangentrum måste summeras direkt till $M$ s tangentrymd vid vilken skärningspunkt som helst. Deras skärningspunkt består alltså av isolerade markerade punkter, dvs ett nolldimensionellt grenrör.
När $\ell _{1}+\ell _{2}>m$ behöver denna summa inte vara direkt. I själva verket kan det inte vara direkt om $f_{1}$ och $f_{2}$ är nedsänkningar vid deras skärningspunkt, vilket händer i fallet med inbäddade undergrenar. Om kartorna är nedsänkningar, kommer skärningen av deras bilder att vara en mångfald av dimension $\ell _{1}+\ell _{2}-m.$

Korsningsprodukt

Givet vilka två släta undergrenrör som helst, är det möjligt att störa endera av dem med en godtyckligt liten mängd så att det resulterande undergrenröret skär tvärs det fasta undergrenröret. Sådana störningar påverkar inte homologiklassen för grenrören eller deras skärningspunkter. Till exempel, om grenrör med komplementär dimension skär tvärsöver, ändras inte den förtecknade summan av antalet skärningspunkter även om vi isotoper grenrören till en annan tvärgående skärningspunkt. (Skärningspunkterna kan räknas modulo 2, ignorera tecknen, för att få en grövre invariant.) Detta går ner till en bilinjär skärningsprodukt på homologiklasser av vilken dimension som helst, vilket är Poincaré- dual till koppprodukten på kohomologi . Precis som koppprodukten är korsningsprodukten graderad kommutativ .

Exempel på tvärgående korsningar

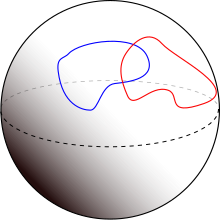
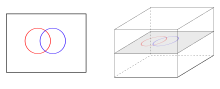
Det enklaste icke-triviala exemplet på transversalitet är bågar i en yta . En skärningspunkt mellan två bågar är tvärgående om och endast om det inte är en tangent, dvs deras tangentlinjer inuti tangentplanet till ytan är distinkta.

I ett tredimensionellt utrymme skär inte tvärgående kurvor varandra. Kurvor tvärs mot ytor skär varandra i punkter, och ytor tvärgående mot varandra skär i kurvor. Kurvor som tangerar en yta vid en punkt (till exempel kurvor som ligger på en yta) skär inte ytan tvärs över.

Här är ett mer specialiserat exempel: anta att $G$ är en enkel Lie-grupp och ${\mathfrak {g}}$ är dess Lie-algebra. Genom Jacobson–Morozovs sats kan varje nilpotent element $e\in {\mathfrak {g}}$ inkluderas i en ${\mathfrak {sl_{2}}}$ -trippel $(e,h,f)$ . Representationsteorin för ${\mathfrak {sl_{2}}}$ säger oss att ${\mathfrak {g}}=[{\mathfrak { g}},e]\oplus {\mathfrak {g}}_{f}$ . Mellanrummet $[{\mathfrak {g}},e]$ är tangentrymden vid $e$ till den angränsande omloppsbanan ${\rm { {Ad}(G)e}}$ och så skär det affina rymden $e+{\mathfrak {g}}_{f}$ banan för $e$ tvärs över. Mellanrummet $e+{\mathfrak {g}}_{f}$ är känt som "Slodowy-skivan" efter Peter Slodowy .

Ansökningar

Optimal kontroll

I fält som använder variationskalkylen eller den relaterade Pontryagin-maximumprincipen , används transversalitetsvillkoret ofta för att kontrollera de typer av lösningar som finns i optimeringsproblem. Till exempel är det ett nödvändigt villkor för lösningskurvor till problem av formen:

Minimera

\int {F(x,y,y^{\prime })}dx

där en eller båda av kurvans ändpunkter inte är fixerade.

I många av dessa problem uppfyller lösningen villkoret att lösningskurvan ska korsa tvärgående nollklinen eller någon annan kurva som beskriver terminalförhållanden.

Jämnhet av lösningsutrymmen

Med hjälp av Sards teorem , vars hypotes är ett specialfall av kartornas transversalitet, kan det visas att tvärgående skärningar mellan undergrenar av ett utrymme med komplementära dimensioner eller mellan undergrenar och kartor till ett utrymme i sig själva är jämna undergrenar. Till exempel, om en jämn sektion av ett orienterat grenrörs tangentbunt – dvs ett vektorfält – ses som en karta från basen till det totala utrymmet och skär nollsektionen (sedd antingen som en karta eller som ett undergrenrör) på tvären , då bildar nolluppsättningen av sektionen – dvs vektorfältets singulariteter – en jämn 0-dimensionell undergren av basen, dvs en uppsättning tecken med tecken. Tecknen överensstämmer med vektorfältets index, och därmed är summan av tecknen – dvs. nollmängdens fundamentalklass – lika med Eulerkarakteristiken för grenröret. Mer generellt, för ett vektorknippe över ett orienterat slätt sluten änddimensionellt grenrör, kommer nolluppsättningen av en sektion tvärs nollsektionen att vara ett undergrenrör av kodimensionens bas lika med rangen för vektorknippet och dess homologiklass kommer att vara Poincaré-dual till Euler-klassen i bunten.

Ett extremt speciellt fall av detta är följande: om en differentierbar funktion från reals till reals har en derivata som inte är noll vid en noll av funktionen, så är nollan enkel, dvs. att grafen är tvärgående mot x -axeln vid den nollpunkten ; en nollderivata skulle betyda en horisontell tangent till kurvan, vilket skulle överensstämma med tangentutrymmet till x -axeln.

För ett oändligt dimensionellt exempel är d-bar-operatorn en sektion av en viss Banach- rymdbunt över utrymmet av kartor från en Riemann-yta till ett nästan komplext grenrör . Nolluppsättningen i detta avsnitt består av holomorfa kartor. Om d-stångsoperatorn kan visas vara tvärgående mot nollsektionen kommer detta modulutrymme att vara ett jämnt grenrör. Dessa överväganden spelar en grundläggande roll i teorin om pseudoholomorfa kurvor och Gromov-Witten-teorin . (Observera att för det här exemplet måste definitionen av transversalitet förfinas för att hantera Banach-utrymmen !)

Grammatik

"Transversal" är ett substantiv; adjektivet är "tvärgående".

citat från JHC Whitehead, 1959

Se även

Transversalitetssats

Anteckningar

Thom, René (1954). "Quelques propriétés globales des variétés differentiables". Comm. Matematik. Helv. 28 (1): 17–86. doi : 10.1007/BF02566923 . S2CID 120243638 .
Guillemin, Victor; Pollack, Alan (1974). Differentiell topologi . Prentice-Hall. ISBN 0-13-212605-2 .
Hirsch, Morris (1976). Differentiell topologi . Springer-Verlag. ISBN 0-387-90148-5 .