Substitutionsmodell

Inom biologin är en substitutionsmodell , även kallad modeller av DNA-sekvensevolution , Markov-modeller som beskriver förändringar över evolutionär tid. Dessa modeller beskriver evolutionära förändringar i makromolekyler (t.ex. DNA-sekvenser ) representerade som sekvens av symboler (A, C, G och T i fallet med DNA ). Substitutionsmodeller används för att beräkna sannolikheten för fylogenetiska träd med hjälp av multipelsekvensinriktningsdata . Således är substitutionsmodeller centrala för maximal sannolikhetsuppskattning av fylogeni såväl som Bayesiansk slutledning i fylogeni . Uppskattningar av evolutionära avstånd (antal substitutioner som har inträffat sedan ett par sekvenser divergerade från en gemensam förfader) beräknas vanligtvis med hjälp av substitutionsmodeller (evolutionära avstånd används för avståndsmetoder som grannsammanfogning ) . Substitutionsmodeller är också centrala för fylogenetiska invarianter eftersom de är nödvändiga för att förutsäga platsmönsterfrekvenser givet en trädtopologi. Substitutionsmodeller är också nödvändiga för att simulera sekvensdata för en grupp av organismer relaterade till ett specifikt träd.

Multipelsekvensanpassning (i detta fall DNA-sekvenser) och illustrationer av användningen av substitutionsmodeller för att dra evolutionära slutsatser. Data i denna justering (i det här fallet ett leksaksexempel med 18 platser) konverteras till en uppsättning platsmönster. Webbplatsmönstren visas tillsammans med antalet gånger de förekommer i linje. Dessa platsmönster används för att beräkna sannolikheten givet substitutionsmodellen och ett fylogenetiskt träd (i detta fall ett orotat fyra-taxonträd). Det är också nödvändigt att anta en substitutionsmodell för att uppskatta evolutionära avstånd för par av sekvenser (avstånd är antalet substitutioner som har inträffat sedan sekvenser hade en gemensam förfader). Den evolutionära distansekvationen ( d ₁₂ ) är baserad på den enkla modell som föreslogs av Jukes och Cantor 1969. Ekvationen transformerar andelen nukleotidskillnader mellan taxa 1 och 2 ( p ₁₂ = 4/18; de fyra platsmönster som skiljer sig mellan taxa 1 och 2 indikeras med asterisker) till ett evolutionärt avstånd (i detta fall d12 = 0,2635 substitutioner per plats) _.

Fylogenetiska trädtopologier och andra parametrar

Fylogenetiska trädtopologier är ofta parametern av intresse; Därför ses grenlängder och andra parametrar som beskriver substitutionsprocessen ofta som störande parametrar . Emellertid är biologer ibland intresserade av de andra aspekterna av modellen. Till exempel grenlängder, särskilt när dessa grenlängder kombineras med information från fossilregistret och en modell för att uppskatta tidsramen för evolutionen. Andra modellparametrar har använts för att få insikter i olika aspekter av evolutionsprocessen. Ka . _/ Ks _- förhållandet (även kallat ω i kodonsubstitutionsmodeller) är en parameter av intresse i många studier K _a /K _s -förhållandet kan användas för att undersöka verkan av naturligt urval på proteinkodande regioner, det ger information om de relativa hastigheterna av nukleotidsubstitutioner som ändrar aminosyror (icke-synonyma substitutioner) till de som inte ändrar kodad aminosyra (synonyma substitutioner).

Applikation för att sekvensera data

Det mesta av arbetet med substitutionsmodeller har fokuserat på DNA/ RNA och proteinsekvensutveckling . Modeller av DNA-sekvensutveckling, där alfabetet motsvarar de fyra nukleotiderna (A, C, G och T), är förmodligen de enklaste modellerna att förstå. DNA-modeller kan också användas för att undersöka RNA-virusutveckling ; detta återspeglar det faktum att RNA också har ett alfabet med fyra nukleotider (A, C, G och U). Ersättningsmodeller kan dock användas för alfabet av alla storlekar; alfabetet är de 20 proteinogena aminosyrorna för proteiner och senskodonen (dvs de 61 kodonen som kodar för aminosyror i den genetiska standardkoden ) för anpassade proteinkodande gensekvenser. Faktum är att substitutionsmodeller kan utvecklas för alla biologiska karaktärer som kan kodas med hjälp av ett specifikt alfabet (t.ex. aminosyrasekvenser kombinerade med information om konformationen av dessa aminosyror i tredimensionella proteinstrukturer ) .

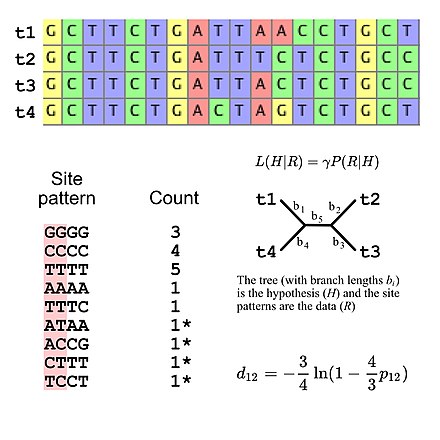
Majoriteten av substitutionsmodellerna som används för evolutionär forskning antar oberoende mellan platser (dvs. sannolikheten för att observera ett specifikt platsmönster är identiskt oavsett var platsmönstret är i sekvensinriktningen). Detta förenklar sannolikhetsberäkningar eftersom det bara är nödvändigt att beräkna sannolikheten för alla platsmönster som visas i anpassningen och sedan använda dessa värden för att beräkna den totala sannolikheten för anpassningen (t.ex. sannolikheten för tre "GGGG"-platsmönster givet någon modell av DNA-sekvensutveckling är helt enkelt sannolikheten för ett enda "GGGG"-ställemönster upphöjt till tredje potens). Detta innebär att substitutionsmodeller kan ses som implicerande en specifik multinomial fördelning för platsmönsterfrekvenser. Om vi ​​betraktar en multipelsekvensinriktning av fyra DNA-sekvenser finns det 256 möjliga platsmönster så det finns 255 frihetsgrader för platsmönsterfrekvenserna. Det är dock möjligt att specificera de förväntade platsmönsterfrekvenserna med hjälp av fem frihetsgrader om man använder Jukes-Cantor-modellen för DNA-evolution, som är en enkel substitutionsmodell som tillåter en att beräkna de förväntade platsmönsterfrekvenserna endast trädtopologin och grenlängder (med fyra taxa har ett orotat grenlängder fem grenlängder).

Substitutionsmodeller gör det också möjligt att simulera sekvensdata med Monte Carlo - metoder . Simulerade multipla sekvensanpassningar kan användas för att bedöma prestandan för fylogenetiska metoder och generera nollfördelningen för vissa statistiska tester inom områdena molekylär evolution och molekylär fylogenetik. Exempel på dessa tester inkluderar tester av modellpassning och "SOWH-testet" som kan användas för att undersöka trädtopologier.

Tillämpning på morfologiska data

Det faktum att substitutionsmodeller kan användas för att analysera alla biologiska alfabet har gjort det möjligt att utveckla evolutionsmodeller för fenotypiska datamängder (t.ex. morfologiska och beteendemässiga egenskaper). Vanligtvis är "0". används för att indikera frånvaron av en egenskap och "1" används för att indikera närvaron av en egenskap, även om det också är möjligt att poängsätta tecken med flera tillstånd. Med detta ramverk kan vi koda en uppsättning fenotyper som binära strängar (detta kan generaliseras till k -tillståndssträngar för tecken med mer än två tillstånd) före analyser med ett lämpligt läge. Detta kan illustreras med ett "leksak"-exempel: vi kan använda ett binärt alfabet för att betygsätta följande fenotypiska egenskaper "har fjädrar", "lägger ägg", "har päls", "är varmblodig" och "kan drivas flyg". I detta leksaksexempel kolibrier ha sekvensen 11011 (de flesta andra fåglar skulle ha samma sträng), strutsar skulle ha sekvensen 11010, nötkreatur (och de flesta andra landdäggdjur ) skulle ha 00110 och fladdermöss skulle ha 00111. Sannolikheten för en fylogenetisk trädet kan sedan beräknas med användning av dessa binära sekvenser och en lämplig substitutionsmodell. Förekomsten av dessa morfologiska modeller gör det möjligt att analysera datamatriser med fossila taxa, antingen med enbart morfologiska data eller en kombination av morfologiska och molekylära data (med de sistnämnda poängsatta som saknade data för fossila taxa).

Det finns en uppenbar likhet mellan användning av molekylära eller fenotypiska data inom området kladistik och analyser av morfologiska karaktärer med hjälp av en substitutionsmodell. Det har dock förekommit en högljudd debatt i systematikersamfundet angående frågan om kladistiska analyser ska ses som "modellfria" eller inte. Området kladistik (definierat i strikt mening) gynnar användningen av maximal sparsamhetskriteriet för fylogenetisk slutledning. Många kladister avvisar ståndpunkten att maximal sparsamhet är baserad på en substitutionsmodell och (i många fall) motiverar de användningen av sparsamhet med Karl Poppers filosofi . Men förekomsten av "parsimony-ekvivalenta" modeller (dvs. substitutionsmodeller som ger det maximala sparsimonyträdet när de används för analyser) gör det möjligt att se parsimony som en substitutionsmodell.

Den molekylära klockan och tidsenheterna

Typiskt uttrycks en grenlängd av ett fylogenetiskt träd som det förväntade antalet substitutioner per plats; om den evolutionära modellen indikerar att varje plats inom en förfäderssekvens typiskt kommer att uppleva x substitutioner när den utvecklas till en viss avkommandes sekvens, så anses förfadern och avkomlingen vara separerade av grenlängden x .

Ibland mäts en grenlängd i termer av geologiska år. Till exempel kan ett fossilregister göra det möjligt att bestämma antalet år mellan en förfäders art och en avkomlig art. Eftersom vissa arter utvecklas i snabbare takt än andra, är dessa två mått på grenlängd inte alltid i direkt proportion. Det förväntade antalet substitutioner per plats och år anges ofta med den grekiska bokstaven mu (μ).

En modell sägs ha en strikt molekylär klocka om det förväntade antalet substitutioner per år μ är konstant oavsett vilken arts utveckling som undersöks. En viktig implikation av en strikt molekylär klocka är att antalet förväntade substitutioner mellan en förfäderart och någon av dess nuvarande avkomlingar måste vara oberoende av vilken avkommansart som undersöks.

Observera att antagandet om en strikt molekylär klocka ofta är orealistiskt, särskilt under långa evolutionsperioder. Till exempel, även om gnagare är genetiskt mycket lika primater , har de genomgått ett mycket högre antal substitutioner under den beräknade tiden sedan divergensen i vissa regioner av genomet . Detta kan bero på deras kortare generationstid , högre ämnesomsättning , ökad populationsstrukturering, ökad artbildning eller mindre kroppsstorlek. När man studerar forntida händelser som den kambriska explosionen under ett antagande av en molekylär klocka, observeras ofta dålig överensstämmelse mellan kldistiska och fylogenetiska data. Det har gjorts en del arbete med modeller som tillåter variabel evolution.

Modeller som kan ta hänsyn till variationen i den molekylära klockans hastighet mellan olika evolutionära linjer i fylogenin kallas "avslappnad" i motsats till "strikt". I sådana modeller kan hastigheten antas vara korrelerad eller inte mellan förfäder och ättlingar och hastighetsvariation mellan linjer kan hämtas från många fördelningar, men vanligtvis används exponentiella och lognormala fördelningar. Det finns ett specialfall, kallat "lokal molekylär klocka" när en fylogeni är uppdelad i minst två partitioner (uppsättningar av linjer) och en strikt molekylär klocka tillämpas i varje, men med olika hastigheter.

Tidsreversibla och stationära modeller

Många användbara substitutionsmodeller är tidsreversibla ; när det gäller matematiken bryr sig modellen inte om vilken sekvens som är förfadern och vilken som är ättling så länge alla andra parametrar (som antalet substitutioner per plats som förväntas mellan de två sekvenserna) hålls konstanta.

När en analys av verkliga biologiska data utförs finns det i allmänhet ingen tillgång till sekvenserna av förfäders arter, bara till dagens arter. Men när en modell är tidsreversibel är vilken art som var den förfäders art irrelevant. Istället kan det fylogenetiska trädet rotas med någon av arterna, rotas om senare baserat på ny kunskap, eller lämnas orotat. Detta beror på att det inte finns någon "speciell" art, alla arter kommer så småningom att härröra från varandra med samma sannolikhet.

En modell är tidsreversibel om och endast om den uppfyller egenskapen (notationen förklaras nedan)

$\pi _{i}Q_{ij}=\pi _{j}Q_{ji}$

eller, på motsvarande sätt, den detaljerade balansegenskapen,

$\pi _{i}P(t)_{ij}=\pi _{j}P(t)_{ji}$

för varje i , j och t .

Tidsreversibilitet ska inte förväxlas med stationaritet . En modell är stationär om Q inte förändras med tiden. Analysen nedan utgår från en stationär modell.

Substitutionsmodellernas matematik

Stationära, neutrala, oberoende, ändliga sitsmodeller (med antagande av en konstant utvecklingshastighet) har två parametrar, π , en jämviktsvektor av bas- (eller karaktärs-) frekvenser och en hastighetsmatris, Q , som beskriver den hastighet med vilken baser av en typ byta till baser av annan typ; element $Q_{ij}$ för i ≠ j är den hastighet med vilken bas i går till bas j . Diagonalerna för Q -matrisen väljs så att raderna summeras till noll:

$Q_{ii}=-{\sum _{\lbrace j\mid j\neq i\rbrace }Q_{ij}}\, ,$

Jämviktsradvektorn π måste förintas av hastighetsmatrisen Q :

$\pi \,Q=0\,.$

Övergångsmatrisfunktionen är en funktion från grenlängderna (i vissa tidsenheter, möjligen i substitutioner), till en matris med villkorade sannolikheter. Den betecknas $P(t)$ . Posten i den i: ^te kolumnen och den j: ^te raden, ${\displaystyle P_{ij}(t)} ,$ är sannolikheten, efter tid t , att det finns en bas j vid en given position, villkorat av att det finns en bas i i den positionen vid tidpunkten 0. När modellen är tidsreversibel kan detta utföras mellan två valfria sekvenser, även om den ena inte är den andras förfader, om du vet den totala grenlängden mellan dem .

De asymptotiska egenskaperna hos P _ij (t) är sådana att P _ij (0) = δ _ij , där δ _ij är Kronecker-deltafunktionen . Det vill säga att det inte finns någon förändring i bassammansättningen mellan en sekvens och sig själv. I den andra ytterligheten, $\lim _{t\rightarrow \infty }P_{ij}(t)=\pi _{j}\,,$ eller, med andra ord, när tiden går till oändligheten går sannolikheten att hitta bas j vid en given position, det fanns en bas i vid den positionen ursprungligen till jämviktssannolikheten att det finns bas j vid den positionen, oavsett den ursprungliga basen. Dessutom följer att $\pi P(t)=\pi$ för alla t .

Övergångsmatrisen kan beräknas från hastighetsmatrisen via matrisexponentiering :

$P(t)=e^{Qt}=\sum _{n=0}^{\infty }Q^{n}{\frac {t^{n}}{n!}}\, ,$

där Q ⁿ är matrisen Q multiplicerad med sig själv tillräckligt många gånger för att ge dess n : ^te potens.

Om Q är diagonaliserbar kan matrisexponentialen beräknas direkt: låt Q = U ⁻¹ Λ U vara en diagonalisering av Q , med

$\Lambda ={\begin{pmatrix}\lambda _{1}&\ldots &0\\\vdots &\ddots &\vdots \\0&\ ldots &\lambda _{4}\end{pmatrix}}\,,$

där Λ är en diagonal matris och där $\lbrace \lambda _{i}\rbrace$ är egenvärdena för Q , vart och ett upprepat enligt sin multiplicitet. Sedan

$P(t)=e^{Qt}=e^{U^{-1} (\Lambda t)U}=U^{-1}e^{\Lambda t}\,U\,,$

där den diagonala matrisen e ^Λt ges av

$e^{\Lambda t}={\begin{pmatrix}e^{\lambda _{1}t}&\ldots &0\\\vdots &\ddots &\vdots \\0&\ldots &e^{ \lambda _{4}t}\end{pmatrix}}\,.$

Generaliserad tid reversibel

Generaliserad tidsreversibel (GTR) är den mest generella neutrala, oberoende, tidsreversibla modellen med ändliga platser. Den beskrevs första gången i allmän form av Simon Tavaré 1986. GTR-modellen kallas ofta för den allmänna tidsreversibla modellen i publikationer; den har också kallats REV-modellen.

GTR-parametrarna för nukleotider består av en jämviktsbasfrekvensvektor, ${\displaystyle {\vec {\pi }}=(\pi _{1},\ pi _{2},\pi _{3},\pi _{4})} ,$ vilket ger den frekvens med vilken varje bas uppträder på varje plats, och hastighetsmatrisen

$Q={\begin{pmatrix}{-(x_{1}+x_{2}+x_{3})} &x_{1}&x_{2}&x_{3}\\{\pi _{1}x_{1} \över \pi _{2}}&{-({\pi _{1}x_{1} \ över \pi _{2}}+x_{4}+x_{5})}&x_{4}&x_{5}\\{\pi _{1}x_{2} \över \pi _{3}} &{\pi _{2}x_{4} \over \pi _{3}}&{-({\pi _{1}x_{2} \over \pi _{3}}+{\pi _ {2}x_{4} \over \pi _{3}}+x_{6})}&x_{6}\\{\pi _{1}x_{3} \over \pi _{4}}& {\pi _{2}x_{5} \over \pi _{4}}&{\pi _{3}x_{6} \over \pi _{4}}&{-({\pi _{ 1}x_{3} \over \pi _{4}}+{\pi _{2}x_{5} \over \pi _{4}}+{\pi _{3}x_{6} \over \pi _{4}})}\end{pmatrix}}$

Eftersom modellen måste vara tidsreversibel och måste närma sig jämviktsnukleotid (bas) frekvenser vid långa tider, är varje hastighet under diagonalen lika med den reciproka hastigheten ovanför diagonalen multiplicerat med jämviktsförhållandet mellan de två baserna. Som sådan kräver nukleotiden GTR 6 parametrar för substitutionshastighet och 4 parametrar för jämviktsbasfrekvens. Eftersom de 4 frekvensparametrarna måste summera till 1 finns det bara 3 lediga frekvensparametrar. Summan av 9 lediga parametrar reduceras ofta ytterligare till 8 parametrar plus $\mu$ , det totala antalet substitutioner per tidsenhet. Vid mätning av tid i substitutioner ( $\mu$ =1) återstår endast 8 lediga parametrar.

I allmänhet, för att beräkna antalet parametrar, räknar du antalet poster ovanför diagonalen i matrisen, dvs för n egenskapsvärden per plats ${{n^{2}-n} \over 2}$ , och addera sedan n-1 för jämviktsfrekvenserna och subtrahera 1 eftersom $\mu$ är fixerad. Du får

${{n^{2}-n} \över 2}+(n-1)-1 ={1 \over 2}n^{2}+{1 \over 2}n-2.$

Till exempel, för en aminosyrasekvens (det finns 20 "standard" aminosyror som utgör proteiner ), skulle du finna att det finns 208 parametrar. När man studerar kodande regioner av genomet är det dock vanligare att arbeta med en kodonsubstitutionsmodell (ett kodon är tre baser och kodar för en aminosyra i ett protein). Det finns $4^{3}=64$ kodoner, vilket resulterar i 2078 fria parametrar. Hastigheterna för övergångar mellan kodoner som skiljer sig med mer än en bas antas dock ofta vara noll, vilket minskar antalet fria parametrar till endast ${{20\times 19\times 3} \over 2}+63-1=632$ parametrar. En annan vanlig praxis är att minska antalet kodoner genom att förbjuda stoppkodonen (eller nonsens) . Detta är ett biologiskt rimligt antagande eftersom att inkludera stoppkodonen skulle innebära att man beräknar sannolikheten för att hitta senskodon $j$ efter tiden $t$ givet att det förfäderliga kodonet är $i$ skulle innebära möjligheten att passera genom ett tillstånd med ett för tidigt stoppkodon.

Ett alternativt (och ofta använt) sätt att skriva den momentana hastighetsmatrisen ( $Q$ -matrisen) för nukleotid-GTR-modellen är:

$Q ={\begin{pmatrix}{-(a\pi _{C}+b\pi _{G}+c\pi _{T})}&a\pi _{C}&b\pi _{G}&c \pi _{T}\\a\pi _{A}&{-(a\pi _{A}+d\pi _{G}+e\pi _{T})}&d\pi _{G }&e\pi _{T}\\b\pi _{A}&d\pi _{C}&{-(b\pi _{A}+d\pi _{C}+f\pi _{T })}&f\pi _{T}\\c\pi _{A}&e\pi _{C}&f\pi _{G}&{-(c\pi _{A}+e\pi _{ C}+f\pi _{G})}\end{pmatrix}}$

Q $Q$ -matrisen är normaliserad så $=1}$${\displaystyle -\sum _{k=1}^{4}\pi _{i}Q_{ii$ .

Denna notation är lättare att förstå än den notation som ursprungligen användes av Tavaré , eftersom alla modellparametrar motsvarar antingen "utbytbarhet"-parametrar ( $a$ till $f$ , som också kan skrivas med notationen $r_{ij}$$\displaystyle {\vec {\pi }}=(\pi _{A} ,\pi _{C},\pi _{G},\pi _{T})}$ eller till jämviktsnukleotidfrekvenser π T . Observera att nukleotiderna i $Q$ -matrisen har skrivits i alfabetisk ordning. Med andra ord skulle övergångssannolikhetsmatrisen för $Q$ -matrisen ovan vara:

$P(t)=e^{Qt}={\begin{pmatrix}p_{\mathrm {AA} }(t)&p_{\mathrm {AC} }(t)&p_ {\mathrm {AG} }(t)&p_{\mathrm {AT} }(t)\\p_{\mathrm {CA} }(t)&p_{\mathrm {CC} }(t)&p_{\mathrm { CG} }(t)&p_{\mathrm {CT} }(t)\\p_{\mathrm {GA} }(t)&p_{\mathrm {GC} }(t)&p_{\mathrm {GG} }( t)&p_{\mathrm {GT} }(t)\\p_{\mathrm {TA} }(t)&p_{\mathrm {TC} }(t)&p_{\mathrm {TG} }(t)&p_{ \mathrm {TT} }(t)\end{pmatrix}}$

Vissa publikationer skriver nukleotiderna i en annan ordning (till exempel, vissa författare väljer att gruppera två puriner tillsammans och de två pyrimidinerna tillsammans; se även modeller för DNA-utveckling ). Dessa skillnader i notation gör det viktigt att vara tydlig med avseende på ordningen på tillstånden när du skriver $Q$ -matrisen.

Värdet av denna notation är att den momentana förändringshastigheten från nukleotid $i$ till nukleotid $j$ alltid kan skrivas som $r_{ij}\pi _{j}$ , där $r_{ij}$ är utbytbarheten av nukleotider $i$ och $j$ och $\pi _{j}$ är jämviktsfrekvensen för nukleotiden $j^{th}$ . Matrisen som visas ovan använder bokstäverna $a$ till $f$ för utbytbarhetsparametrarna i läsbarhetens intresse, men dessa parametrar kan också skrivas på ett systematiskt sätt med hjälp av $r_{ij}$ notation (t.ex. $a=r_{AC}$ , $b=r_{AG}$ och så vidare).

Observera att ordningen av nukleotidunderskrifterna för utbytbarhetsparametrar är irrelevant (t.ex. $r_{AC}=r_{CA}$ ) men övergångssannolikhetsmatrisvärdena är inte det (dvs. $p_{\mathrm {AC} }(t)$ är sannolikheten att observera A i sekvens 1 och C i sekvens 2 när det evolutionära avståndet mellan dessa sekvenser är $t$ medan $p_{\mathrm {CA} }(t)$ är sannolikheten att observera C i sekvens 1 och A i sekvens 2 på samma evolutionära avstånd).

En godtyckligt valda utbytbarhetsparametrar (t.ex. $f=r_{GT}$ ) ställs vanligtvis in på värdet 1 för att öka läsbarheten för uppskattningarna av utbytbarhetsparametrar (eftersom den tillåter användare att uttrycka dessa värden i förhållande till vald utbytbarhetsparameter). Praktiken att uttrycka utbytbarhetsparametrarna i relativa termer är inte problematisk eftersom $Q$ -matrisen är normaliserad. Normalisering tillåter $t$ (tid) i matrisexponentieringen $P(t)=e^{Qt}$ att uttryckas i enheter av förväntade substitutioner per plats (standardpraxis i molekylär fylogenetik). Detta motsvarar påståendet att man ställer in mutationshastigheten $\mu$ till 1) och minskar antalet fria parametrar till åtta. Specifikt finns det fem fria utbytbarhetsparametrar ( $a$ till $e$ , som uttrycks i förhållande till den fasta $f=r_{GT}=1$ i detta exempel) och tre jämviktsbasfrekvensparametrar (som beskrivits ovan behöver endast tre ${\displaystyle \pi _{i}}-$ värden anges eftersom ${\vec {\pi }}$ måste summera till 1).

Den alternativa notationen gör det också lättare att förstå delmodellerna av GTR-modellen, som helt enkelt motsvarar fall där utbytbarhet och/eller jämviktsbasfrekvensparametrar är begränsade till att anta lika värden. Ett antal specifika undermodeller har namngetts, till stor del baserat på deras ursprungliga publikationer:

Utvalda modeller av DNA-utveckling som ofta används inom molekylär fylogenetik

Modell	Utbytbarhetsparametrar	Basfrekvensparametrar	Referens
JC69 (eller JC)	$a=b=c=d=e=f$	$\pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25$	Jukes and Cantor (1969)
F81	$a=b=c=d=e=f$	alla $\pi _{i}$ värden är fria	Felsenstein (1981)
K2P (eller K80)	$a=c=d=f$ ( transversioner ), $b=e$ ( övergångar )	$\pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25$	Kimura (1980)
HKY85	$a=c=d=f$ ( transversioner ), $b=e$ ( övergångar )	alla $\pi _{i}$ värden är fria	Hasegawa et al. (1985)
K3ST (eller K81)	$a=f$ ( $\gamma$ transversioner ), $c=d$ ( $\beta$ transversioner ), $b= e$ ( övergångar )	$\pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25$	Kimura (1981)
TN93	$a=c=d=f$ ( transversioner ), $b$ ( $A\leftrightarrow G$ övergångar ), $e$ ( $C\leftrightarrow T$ övergångar )	alla $\pi _{i}$ värden är fria	Tamura och Nei (1993)
SYM	alla utbytbarhetsparametrar fria	$\pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25$	Zharkikh (1994)
GTR (eller REV)	alla utbytbarhetsparametrar fria	alla $\pi _{i}$ värden är fria	Tavaré (1986)

Det finns 203 möjliga sätt som utbytbarhetsparametrarna kan begränsas till att bilda undermodeller av GTR, allt från JC69- och F81-modellerna (där alla utbytbarhetsparametrar är lika) till SYM-modellen och den fullständiga GTR (eller REV)-modellen (där alla utbytbarhetsparametrar är gratis). Jämviktsbasfrekvenserna behandlas vanligtvis på två olika sätt: 1) alla ${\displaystyle \pi _{i}}-$ värden är begränsade till att vara lika (dvs ${ \displaystyle \pi _{A}=\pi _{C}=\pi _{G}=\pi _{T}=0.25} )$ ; eller 2) alla $\pi _{i}$ -värden behandlas som fria parametrar. Även om jämviktsbasfrekvenserna kan begränsas på andra sätt är de flesta begränsningar som länkar några men inte alla ${\displaystyle \pi _{i}}-$ värden orealistiska ur biologisk synvinkel. Det möjliga undantaget är att framtvinga strängsymmetri (dvs att begränsa $\pi _{A}=\pi _{T}$ och $\pi _{C}=\ pi _{G}$ men tillåter $\pi _{A}+\pi _{T}\neq \pi _{C}+\pi _{G}$ ).

Den alternativa notationen gör det också enkelt att se hur GTR-modellen kan tillämpas på biologiska alfabet med ett större tillståndsutrymme (t.ex. aminosyror eller kodon ). Det är möjligt att skriva en uppsättning jämviktstillståndsfrekvenser som $\pi _{1}$ , $\pi _{2}$ , ... $\pi _{ k}$ och en uppsättning utbytbarhetsparametrar ( $r_{ij}$ ) för alla alfabet av $k$ teckentillstånd. Dessa värden kan användas för att fylla i $Q$ -matrisen genom att ställa in de off-diagonala elementen som visas ovan (den allmänna notationen skulle vara $Q_{ij}=r_ {ij}\pi _{j}$ ), sätter de diagonala elementen $Q_{ii}$ till den negativa summan av de off-diagonala elementen på samma rad, och normaliserar. Uppenbarligen är $k=20$ för aminosyror och $k=61$ för kodon (under antagande av den genetiska standardkoden ). Allmänheten i denna notation är dock fördelaktig eftersom man kan använda reducerade alfabet för aminosyror. Till exempel kan man använda $k=6$ och koda för aminosyror genom att koda om aminosyrorna med de sex kategorier som föreslås av Margaret Dayhoff . Reducerade aminosyraalfabet ses som ett sätt att minska påverkan av sammansättningsvariationer och mättnad.

Mekanistiska vs. empiriska modeller

En huvudskillnad i evolutionära modeller är hur många parametrar som uppskattas varje gång för datamängden i fråga och hur många av dem som uppskattas en gång på en stor datamängd. Mekanistiska modeller beskriver alla substitutioner som en funktion av ett antal parametrar som uppskattas för varje datauppsättning som analyseras, helst med maximal sannolikhet . Detta har fördelen att modellen kan anpassas till särdragen hos en specifik datamängd (t.ex. olika sammansättningsförändringar i DNA). Problem kan uppstå när för många parametrar används, särskilt om de kan kompensera för varandra (detta kan leda till icke-identifierbarhet). Då är det ofta så att datamängden är för liten för att ge tillräckligt med information för att uppskatta alla parametrar korrekt.

Empiriska modeller skapas genom att uppskatta många parametrar (vanligtvis alla inmatningar av hastighetsmatrisen såväl som teckenfrekvenserna, se GTR-modellen ovan) från en stor datamängd. Dessa parametrar är sedan fasta och kommer att återanvändas för varje datamängd. Detta har fördelen att dessa parametrar kan uppskattas mer exakt. Normalt är det inte möjligt att uppskatta alla poster i substitutionsmatrisen endast från den aktuella datamängden. På nackdelen kan parametrarna som uppskattas från träningsdata vara för generiska och därför ha en dålig anpassning till en viss datauppsättning. En potentiell lösning på det problemet är att uppskatta vissa parametrar från data med maximal sannolikhet (eller någon annan metod). I studier av proteinutveckling är jämviktsaminosyrafrekvenserna ${\displaystyle {\vec {\pi }}=(\pi _{A},\ pi _{R},\pi _{N},...\pi _{V})} ($ med enbokstavs IUPAC-koder för aminosyror för att indikera deras jämviktsfrekvenser) uppskattas ofta från data samtidigt som utbytbarhetsmatris fixerad. Utöver den vanliga praxisen att uppskatta aminosyrafrekvenser från data, har metoder för att uppskatta utbytbarhetsparametrar eller justera $Q$ -matrisen för proteinutveckling på andra sätt föreslagits.

Med den storskaliga genomsekvenseringen fortfarande producerar mycket stora mängder DNA- och proteinsekvenser, finns det tillräckligt med data tillgänglig för att skapa empiriska modeller med valfritt antal parametrar, inklusive empiriska kodonmodeller. På grund av problemen som nämnts ovan kombineras de två tillvägagångssätten ofta genom att de flesta parametrarna uppskattas en gång på storskalig data, medan ett fåtal återstående parametrar sedan justeras till den datauppsättning som övervägs. Följande avsnitt ger en översikt över de olika tillvägagångssätten för DNA-, protein- eller kodonbaserade modeller.

DNA-substitutionsmodeller

Huvudartikel: Modeller av DNA-evolution

De första modellerna för DNA-evolution föreslogs Jukes och Cantor 1969. Jukes-Cantor-modellen (JC eller JC69) antar lika övergångshastigheter såväl som lika jämviktsfrekvenser för alla baser och det är den enklaste undermodellen av GTR-modellen. 1980 Motoo Kimura en modell med två parametrar (K2P eller K80): en för övergången och en för transversionshastigheten . Ett år senare Kimura en andra modell (K3ST, K3P eller K81) med tre substitutionstyper: en för övergångshastigheten, en för hastigheten för transversioner som bevarar de starka/svaga egenskaperna hos nukleotider ( $A\leftrightarrow T$ och $C\leftrightarrow G$ , betecknade $\beta$ av Kimura), och en för transversionshastigheten som bevarar amino/keto-egenskaperna hos nukleotider ( ${ \displaystyle A\leftrightarrow C}$ och $G\leftrightarrow T$ , betecknade $\gamma$ av Kimura). Joseph Felsenstein föreslog 1981 en modell med fyra parametrar (F81) där substitutionshastigheten motsvarar målnukleotidens jämviktsfrekvens. Hasegawa, Kishino och Yano förenade de två sista modellerna till en femparametersmodell (HKY). Efter dessa banbrytande ansträngningar introducerades många ytterligare undermodeller av GTR-modellen i litteraturen (och allmänt bruk) på 1990-talet. Andra modeller som går bortom GTR-modellen på specifika sätt har också utvecklats och förfinats av flera forskare.

Nästan alla DNA-substitutionsmodeller är mekanistiska modeller (som beskrivits ovan). Det lilla antalet parametrar som man behöver uppskatta för dessa modeller gör det möjligt att uppskatta dessa parametrar från data. Det är också nödvändigt eftersom mönstren för utveckling av DNA-sekvenser ofta skiljer sig åt mellan organismer och bland gener inom organismer. Det senare kan återspegla optimering genom verkan av selektion för specifika ändamål (t.ex. snabbt uttryck eller budbärar-RNA-stabilitet) eller så kan det återspegla neutral variation i substitutionsmönstren. Beroende på organismen och typen av gen är det således sannolikt nödvändigt att anpassa modellen till dessa omständigheter.

Tvåstatssubstitutionsmodeller

Ett alternativt sätt att analysera DNA-sekvensdata är att koda om nukleotiderna som puriner (R) och pyrimidiner (Y); denna praxis kallas ofta RY-kodning. Insättningar och deletioner i multipla sekvensanpassningar kan också kodas som binära data och analyseras med hjälp av en tvåtillståndsmodell.

Den enklaste tvåtillståndsmodellen för sekvensutveckling kallas Cavender-Farris-modellen eller Cavender-Farris- Neyman (CFN)-modellen; namnet på denna modell återspeglar det faktum att den har beskrivits oberoende av varandra i flera olika publikationer. CFN-modellen är identisk med Jukes-Cantor-modellen anpassad till två tillstånd och den har till och med implementerats som "JC2"-modellen i det populära mjukvarupaketet IQ-TREE (att använda denna modell i IQ-TREE kräver kodning av data som 0 och 1 snarare än R och Y; det populära mjukvarupaketet PAUP* kan tolka en datamatris som endast omfattar R och Y som data som ska analyseras med CFN-modellen). Det är också enkelt att analysera binära data med hjälp av den fylogenetiska Hadamard-transformen . Den alternativa tvåtillståndsmodellen tillåter jämviktsfrekvensparametrarna för R och Y (eller 0 och 1) att anta andra värden än 0,5 genom att lägga till en enda fri parameter; denna modell kallas på olika sätt CFu eller GTR2 (i IQ-TREE).

Aminosyrasubstitutionsmodeller

För många analyser, särskilt för längre evolutionära avstånd, är utvecklingen modellerad på aminosyranivå. Eftersom inte all DNA-substitution också förändrar den kodade aminosyran, går information förlorad när man tittar på aminosyror istället för nukleotidbaser. Flera fördelar talar dock för att använda aminosyrainformationen: DNA är mycket mer benäget att visa sammansättningsbias än aminosyror, alla positioner i DNA:t utvecklas inte med samma hastighet (icke-synonyma mutationer är mindre benägna att fixeras i befolkningen än synonyma ), men förmodligen viktigast, på grund av de snabba utvecklingspositionerna och den begränsade alfabetets storlek (endast fyra möjliga tillstånd), lider DNA av fler ryggsubstitutioner, vilket gör det svårt att exakt uppskatta evolutionära längre avstånd.

Till skillnad från DNA-modellerna är aminosyramodeller traditionellt empiriska modeller. De var pionjärer på 1960- och 1970-talen av Dayhoff och medarbetare genom att uppskatta ersättningsfrekvenser från proteinanpassningar med minst 85% identitet (ursprungligen med mycket begränsade data och slutligen kulminerade i Dayhoff PAM -modellen från 1978). Detta minimerade chanserna att observera flera substitutioner på en plats. Från den uppskattade hastighetsmatrisen härleddes en serie ersättningssannolikhetsmatriser, kända under namn som PAM 250. Logoddsmatriser baserade på Dayhoff PAM -modellen användes vanligtvis för att bedöma signifikansen av homologisökresultat, även om BLOSUM - matriserna har ersatte PAM -logoddsmatriserna i detta sammanhang eftersom BLOSUM-matriserna verkar vara känsligare över en mängd olika evolutionära avstånd, till skillnad från PAM- logoddsmatriserna .

Dayhoff PAM-matrisen var källan till utbytbarhetsparametrarna som användes i en av de första maximala sannolikhetsanalyserna av fylogeni som använde proteindata och PAM-modellen (eller en förbättrad version av PAM-modellen kallad DCMut) fortsätter att användas inom fylogenetiken. Det begränsade antalet anpassningar som användes för att generera PAM-modellen (som återspeglar den begränsade mängden sekvensdata som fanns tillgänglig på 1970-talet) ökade dock nästan säkert variansen av vissa hastighetsmatrisparametrar (alternativt kunde de proteiner som användes för att generera PAM-modellen ha varit en icke-representativ uppsättning). Oavsett vilket är det tydligt att PAM-modellen sällan passar lika bra till de flesta datauppsättningar som mer moderna empiriska modeller (Keane et al. 2006 testade tusentals ryggrads-, bakterie- och arkeala proteiner och de fann att Dayhoff PAM-modellen hade bäst passar till högst <4 % av proteinerna).

Från och med 1990-talet ledde den snabba expansionen av sekvensdatabaser på grund av förbättrad sekvenseringsteknik till uppskattning av många nya empiriska matriser (se för en fullständig lista). De tidigaste försöken använde metoder som liknar dem som användes av Dayhoff, med storskalig matchning av proteindatabasen för att generera en ny logoddsmatris och JTT-modellen (Jones-Taylor-Thornton). De snabba ökningarna i beräkningskraft under denna tid (som återspeglar faktorer som Moores lag ) gjorde det möjligt att uppskatta parametrar för empiriska modeller med maximal sannolikhet (t.ex. WAG- och LG-modellerna) och andra metoder (t.ex. VT- och PMB-modellerna) . Programvarupaketet IQ-Tree låter användare härleda sin egen tidsreversibla modell med QMaker, eller icke-tidsreversibel med nQMaker.

En annan uppsättning substitutionsmodeller för proteinevolution inkluderar direkt information från proteinstrukturen och ger en mer realistisk modellering när det gäller sannolikhet och biologisk betydelse.

No Common Mechanism (NCM)-modellen och maximal sparsamhet

1997 beskrev Tuffley och Steel en modell som de kallade modellen för no common mechanism (NCM). Topologin för det maximala sannolikhetsträdet för en specifik datauppsättning givet NCM-modellen är identisk med topologin för det optimala trädet för samma data givet det maximala sparsamhetskriteriet . NCM-modellen antar att alla data (t.ex. homologa nukleotider, aminosyror eller morfologiska karaktärer) är relaterade till ett vanligt fylogenetiskt träd. Sedan introduceras ${\displaystyle 2T-3} parametrar för varje homologt tecken, där$$T$ är antalet sekvenser. Detta kan ses som en uppskattning av en separat hastighetsparameter för varje tecken × grenpar i datamängden (observera att antalet grenar i ett fullt upplöst fylogenetiskt träd är 2 T − 3 {\ $} )$ . Således överstiger antalet fria parametrar i NCM-modellen alltid antalet homologa tecken i datamatrisen, och NCM-modellen har kritiserats som konsekvent "överparameteriserad".

externa länkar

• Empiriska modeller för aminosyrasubstitution