Steiner kedja

Figur 1: En Steiner-kedja med tolv svarta cirklar

(n = 12)

. De givna cirklarna visas i blått och rött, vilket är de yttersta respektive innersta cirklarna.

Inom geometri är en Steinerkedja en uppsättning av $n$ cirklar, som alla tangerar två givna icke-korsande cirklar (blå och röd i figur 1), där $n$ är ändlig och varje cirkel i kedjan tangerar den föregående och nästa cirklar i kedjan. I de vanliga slutna Steiner-kedjorna är de första och sista ( $n$ -:te) cirklarna också tangenter till varandra; i öppna Steiner-kedjor behöver de däremot inte vara det. De givna cirklarna $α$ och $β$ skär inte varandra, men i övrigt är de obegränsade; den mindre cirkeln kan ligga helt innanför eller utanför den större cirkeln. I dessa fall ligger mitten av Steiner-kedjans cirklar på en ellips respektive en hyperbel .

Steiner-kedjor är uppkallade efter Jakob Steiner , som definierade dem på 1800-talet och upptäckte många av deras egenskaper. Ett grundläggande resultat är Steiners porism , som säger:

Om åtminstone en sluten Steinerkedja med

n

cirklar existerar för två givna cirklar

α

och

β

, så finns det ett oändligt antal slutna Steinerkedjor med

n

cirklar; och varje cirkel som tangerar

α

och

β

på samma sätt är en medlem av en sådan kedja.

Metoden för cirkelinversion är till hjälp vid behandling av Steiner-kedjor. Eftersom den bevarar tangenser, vinklar och cirklar, omvandlar inversion en Steiner-kedja till en annan med samma antal cirklar. Ett särskilt val av inversion omvandlar de givna cirklarna $α$ och $β$ till koncentriska cirklar; i detta fall har alla cirklar i Steinerkedjan samma storlek och kan "rulla" runt i ringen mellan cirklarna liknande kullager . Denna standardkonfiguration gör det möjligt att härleda flera egenskaper hos Steiner-kedjor, t.ex. dess tangenspunkter ligger alltid på en cirkel. Det finns flera generaliseringar av Steiner-kedjor, mest notably Soddy's hexlet och Pappus-kedjor .

Definitioner och typer av tangens

Steiner-kedjor med olika interna/externa tangenser
De 7 cirklarna i denna Steinerkedja (svart) tangerar externt den inre givna cirkeln (röd) men tangerar internt till den yttre givna cirkeln (blå).
De 7 cirklarna i denna Steinerkedja (svart) tangerar externt båda givna cirklarna (röd och blå), som ligger utanför varandra.
Sju av de 8 cirklarna i denna Steinerkedja (svart) är externt tangenter till båda givna cirklarna (röd och blå); den 8:e cirkeln är internt tangent till båda.

De två givna cirklarna α och β kan inte skära varandra; därför måste den mindre givna cirkeln ligga innanför eller utanför den större. Cirklarna visas vanligtvis som en annulus , dvs med den mindre givna cirkeln inuti den större. I denna konfiguration tangerar Steiner-kedjans cirklar externt till den inre givna cirkeln och internt tangent till den yttre cirkeln. Den mindre cirkeln kan dock också ligga helt utanför den större (Figur 2). De svarta cirklarna i figur 2 uppfyller villkoren för en sluten Steiner-kedja: de tangerar alla de två givna cirklarna och var och en tangerar sina grannar i kedjan. I denna konfiguration har Steiner-kedjans cirklar samma typ av tangens till båda givna cirklarna, antingen externt eller internt som tangerar båda. Om de två givna cirklarna tangerar i en punkt, blir Steinerkedjan en oändlig Pappuskedja , vilket ofta diskuteras i samband med arbelos ( skomakarkniv ), en geometrisk figur gjord av tre cirklar. Det finns inget allmänt namn för en serie cirklar som tangerar två givna cirklar som skär varandra i två punkter.

Stängd, öppen och multicyklisk

Stängda, öppna och multicykliska Steiner-kedjor
Sluten Steinerkedja med nio cirklar. De 1:a och 9:e cirklarna är tangenter.
Öppna Steiner-kedja med nio cirklar. De 1:a och 9:e cirklarna överlappar varandra.
Multicyklisk Steiner-kedja med 17 cirklar i 2 omslag. De 1:a och 17:e cirklarna berör.

De två givna cirklarna α och β berör de n cirklarna i Steinerkedjan, men varje cirkel C _k i en Steinerkedja berör endast fyra cirklar: α , β , och dess två grannar, C _{k −1} och C _{k +1} . Som standard antas Steiner-kedjor vara slutna , dvs. de första och sista cirklarna tangerar varandra. Däremot är en öppen Steinerkedja en där de första och sista cirklarna, C ₁ och C _n , inte tangerar varandra; dessa cirklar tangerar endast tre cirklar. Multicykliska Steiner-kedjor lindas runt den inre cirkeln mer än en gång innan de sluter sig, dvs innan de tangerar den initiala cirkeln.

Slutna Steiner-kedjor är de system av cirklar som erhålls som cirkelpackningssatsen representation av en bipyramid .

Annulärt fall och genomförbarhetskriterium

Ringformade Steiner-kedjor
n = 3
n = 6
n = 9
n = 12
n = 20

Radien för Steinercirklarna är ρ medan de för de inre och yttre givna cirklarna är r respektive R . Avståndet från mitten av den inre cirkeln till mitten av en Steinercirkel är r + ρ (orange linjesegment).

Den enklaste typen av Steinerkedja är en sluten kedja av n lika stora cirklar som omger en inskriven cirkel med radien r ; cirkelkedjan är själv omgiven av en omskriven cirkel med radien R . De inskrivna och omskrivna givna cirklarna är koncentriska, och Steiner-kedjans cirklar ligger i ringen mellan dem. Genom symmetri är vinkeln 2 θ mellan mitten av Steiner-kedjans cirklar 360°/ n . Eftersom Steiner-kedjecirklar tangerar varandra, är avståndet mellan deras centra lika med summan av deras radier, här två gånger deras radie ρ . Bisektrisen (grön i figuren) skapar två räta trianglar, med en mittvinkel på θ = 180°/ n . Sinus för denna vinkel kan skrivas som längden av dess motsatta segment, dividerat med hypotenusan i den räta triangeln

\sin \theta ={\frac {\rho }{r+\rho }}

Eftersom θ är känd från n ger detta en ekvation för den okända radien ρ för Steiner-kedjans cirklar

\rho ={\frac {r\sin \theta }{1-\sin \theta }}

Tangentpunkterna för en Steiner-kedjecirkel med de inre och yttre givna cirklarna ligger på en linje som går genom deras gemensamma centrum; därför är den yttre radien R = r + 2 ρ .

Dessa ekvationer ger ett kriterium för genomförbarheten av en Steinerkedja för två givna koncentriska cirklar. En sluten Steinerkedja med n cirklar kräver att förhållandet mellan radierna R / r för de givna cirklarna är exakt lika med

{\frac {R}{r}}= 1+{\frac {2\sin \theta }{1-\sin \theta }}={\frac {1+\sin \theta }{1-\sin \theta }}=\left[\sec \theta +\tan \theta \right]^{2}

Som visas nedan kan detta radie-förhållandekriterium för koncentriska givna cirklar utvidgas till alla typer av givna cirklar med det inversiva avståndet δ för de två givna cirklarna. För koncentriska cirklar definieras detta avstånd som en logaritm av deras förhållande mellan radier

\delta =\ln {\frac {R}{r}}

Med hjälp av lösningen för koncentriska cirklar kan det allmänna kriteriet för en Steinerkedja med n cirklar skrivas

\delta =2\ln \left(\sec \theta +\tan \theta \right).

Om en multicyklisk ringformad Steiner-kedja har totalt n cirklar och lindas runt m gånger innan den stängs, är vinkeln mellan Steiner-kedjans cirklar lika med

\theta ={\frac {m}{n}}180^{\circ }

I övrigt är genomförbarhetskriteriet oförändrat.

Egenskaper under inversion

Inversiva egenskaper hos Steiner-kedjor
Två cirklar (rosa och cyan) som internt tangerar båda givna cirklarna och vars centrum är i linje med mitten av de givna cirklarna skär i vinkeln 2 θ .
Under inversion blir dessa linjer och cirklar cirklar med samma skärningsvinkel, 2 θ . Guldcirklarna skär de två givna cirklarna i räta vinklar, dvs ortogonalt.
Cirklarna som passerar genom de ömsesidiga tangentpunkterna för Steiner-kedjans cirklar är ortogonala mot de två givna cirklarna och skär varandra vid multiplar av vinkeln 2 θ .
De cirklar som passerar genom tangentpunkterna för Steiner-kedjans cirklar med de två givna cirklarna är ortogonala mot den senare och skär varandra vid multiplar av vinkeln 2 θ .

Cirkelinversion omvandlar en Steinerkedja till en annan med samma antal cirklar.

I den transformerade kedjan ligger tangentpunkterna mellan angränsande cirklar i Steinerkedjan alla på en cirkel, nämligen den koncentriska cirkeln mitt emellan de två fasta koncentriska cirklarna. Eftersom tangenser och cirklar bevaras under inversion, är denna egenskap hos alla tangenser som ligger på en cirkel också sant i den ursprungliga kedjan. Denna egenskap delas också med Pappus kedja av cirklar, vilket kan tolkas som ett speciellt begränsande fall av Steiner-kedjan.

I den transformerade kedjan är tangentlinjerna från O till Steinerkedjecirklarna åtskilda av lika vinklar. I den ursprungliga kedjan motsvarar detta lika stora vinklar mellan tangentcirklarna som passerar genom inversionscentrum som används för att omvandla de ursprungliga cirklarna till ett koncentriskt par.

I den transformerade kedjan går de n linjerna som förbinder paren av tangentpunkter i Steinercirklarna med de koncentriska cirklarna genom O , det gemensamma centrumet. På liknande sätt passerar de n linjerna som tangerar varje par av angränsande cirklar i Steinerkedjan också genom O . Eftersom linjer genom inversionscentrum är invarianta under inversion, och eftersom tangens och samtidighet bevaras under inversion, passerar de 2 n linjerna som förbinder motsvarande punkter i den ursprungliga kedjan också genom en enda punkt, O .

Oändlig familj

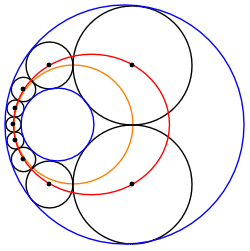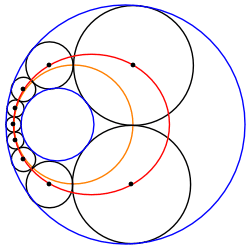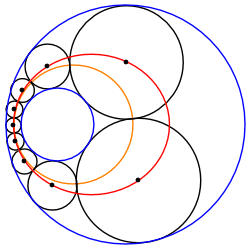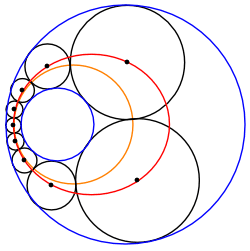
Om ens en sluten Steiner-kedja är möjlig för två givna cirklar (blå), så är oändligt många Steiner-kedjor möjliga, alla relaterade genom rotation. Deras tangenspunkter faller alltid på en cirkel (orange). Om de två givna cirklarna är kapslade, den ena inuti den andra, faller mitten av Steinerkedjecirklarna (svart) på en ellips (röd); annars faller de på en hyperbel .

En Steinerkedja mellan två icke-korsande cirklar kan alltid omvandlas till en annan Steinerkedja av lika stora cirklar inklämda mellan två koncentriska cirklar. Därför tillhör varje sådan Steiner-kedja till en oändlig familj av Steiner-kedjor relaterade genom rotation av den transformerade kedjan kring O , det gemensamma centrumet för de transformerade gränscirklarna.

Elliptiska/hyperboliska centras locus

Mitten av cirklarna i en Steinerkedja ligger på en konisk sektion . Till exempel, om den mindre givna cirkeln ligger inom den större, ligger mitten på en ellips . Detta gäller för alla uppsättningar cirklar som internt tangerar en given cirkel och externt tangerar den andra; sådana system av cirklar visas i Pappus-kedjan , problemet med Apollonius och den tredimensionella Soddy's hexlet . På liknande sätt, om vissa cirklar i Steinerkedjan externt tangerar båda givna cirklarna, måste deras centra ligga på en hyperbel, medan de som internt tangerar båda ligger på en annan hyperbel.

Steinerkedjans cirklar tangerar två fasta cirklar, här betecknade α och β , där β omges av α . Låt radierna för dessa två cirklar betecknas som r _α respektive r _β , och låt deras respektive centrum vara punkterna A och B . Låt radien, diametern och mittpunkten för Steinerkedjans k : ^{te cirkel betecknas som} r _k , d _k respektive P _k .

Alla centra i cirklarna i Steinerkedjan är belägna på en vanlig ellips , av följande anledning. Summan av avstånden från mittpunkten i den k: ^te cirkeln i Steinerkedjan till de två mittpunkterna A och B i de fasta cirklarna är lika med en konstant

{\overline {\mathbf {P} _{k}\mathbf { A} }}+{\overline {\mathbf {P} _{k}\mathbf {B} }}=(r_{\alpha }-r_{k})+\left(r_{\beta }+r_{ k}\right)=r_{\alpha }+r_{\beta }

Sålunda, för alla centra i Steinerkedjans cirklar, är summan av avstånden till A och B lika med samma konstant, r _α + r _β . Detta definierar en ellips, vars två brännpunkter är punkterna A och B , cirklarnas mittpunkter, α och β , som lägger samman Steinerkedjan av cirklar.

Summan av avstånden till brännpunkterna är lika med två gånger halvstoraxeln a för en ellips; därav,

2a=r_{\alpha }+r_{\beta }

Låt p vara lika med avståndet mellan brännpunkterna, A och B . Sedan definieras excentriciteten e av 2 ae = p , eller

e={\frac {p}{2a}}={\frac {p}{r_{\alpha }+r_{\beta }}}

Från dessa parametrar kan semi-minoraxeln b och semi-latus rektum L bestämmas

b^{2}=a^{2}\left(1-e^{2}\right)=a^{2 }-{\frac {p^{2}}{4}}

L={\frac {b^{2}}{a}}=a -{\frac {p^{2}}{4a}}

Därför kan ellipsen beskrivas med en ekvation i termer av dess avstånd d till ett fokus

d={\frac {L}{1-e\cos \theta }}

där θ är vinkeln med linjen som förenar de två brännpunkterna.

Konjugerade kedjor

Konjugera Steiner-kedjor med n = 4
Steinerkedja med de två givna cirklarna i rött och blått.
Samma uppsättning cirklar, men med ett annat val av givna cirklar.
Samma uppsättning cirklar, men med ytterligare ett val av givna cirklar.

Om en Steinerkedja har ett jämnt antal cirklar, så kan alla två diametralt motsatta cirklar i kedjan tas som de två givna cirklarna i en ny Steinerkedja som de ursprungliga cirklarna tillhör. Om den ursprungliga Steiner-kedjan har n cirklar i m omslag, och den nya kedjan har p -cirklar i q -omslag, så gäller ekvationen

{\frac {m}{n}}+{\frac {p}{q}}={\frac {1}{2}}.

Ett enkelt exempel förekommer för Steiner-kedjor med fyra cirklar ( n = 4) och en omslag ( m = 1). I detta fall är de givna cirklarna och Steiner-kedjans cirklar ekvivalenta genom att båda typerna av cirklar tangerar fyra andra; mer allmänt tangerar Steiner-kedjans cirklar fyra cirklar, men de två givna cirklarna tangerar n cirklar. I det här fallet kan valfritt par av motsatta medlemmar av Steinerkedjan väljas som de givna cirklarna i en annan Steinerkedja som involverar de ursprungliga givna cirklarna. Eftersom m = p = 1 och n = q = 4, är Steiners ekvation uppfylld:

{\frac {1}{4}}+{\frac {1}{4}}={\frac {1}{2}}.

Generaliseringar

Soddy's hexlet är en tredimensionell analog av Steinerkedjan.

Den enklaste generaliseringen av en Steinerkedja är att låta de givna cirklarna röra eller skära varandra. I det förra fallet motsvarar detta en Pappus-kedja , som har ett oändligt antal cirklar.

Soddys hexlet är en tredimensionell generalisering av en Steinerkedja med sex cirklar. De sex sfärernas centra ( hexlet ) färdas längs samma ellips som centran för motsvarande Steiner-kedja. Höljet av hexlet-sfärerna är en Dupin-cyklid , inversionen av en torus . De sex sfärerna tangerar inte bara den inre och yttre sfären, utan också till två andra sfärer, centrerade ovanför och under planet för hexlet-centrum.

Flera ringar av Steiner-kedjor är en annan generalisering. En vanlig Steinerkedja erhålls genom att invertera en ringformig kedja av tangentcirklar som begränsas av två koncentriska cirklar. Detta kan generaliseras till att invertera tre eller flera koncentriska cirklar som lägger in ringformade kedjor av tangentcirklar.

Hierarkiska Steiner-kedjor är ännu en generalisering. Om de två givna cirklarna i en vanlig Steinerkedja är kapslade, dvs om den ena ligger helt inom den andra, så omsluter den större givna cirkeln Steinerkedjans cirklar. I en hierarkisk Steinerkedja är varje cirkel i en Steinerkedja i sig den omskrivande givna cirkeln för en annan Steinerkedja inom den; denna process kan upprepas på obestämd tid och bilda en fraktal .

Se även

Anteckningar

Bibliografi

Ogilvy, CS (1990). Utflykter i geometri . Dover. s. 51–54 . ISBN 0-486-26530-7 .
Coxeter, HSM ; Greitzer, SL (1967). Geometri Revisited . Nytt matematiskt bibliotek. Vol. 19. Washington : MAA . s. 123–126, 175–176, 180. ISBN 978-0-88385-619-2 . Zbl 0166.16402 .
Johnson RA (1960). Advanced Euclidean Geometry: En elementär avhandling om triangelns och cirkelns geometri (omtryck av 1929 års upplaga av Houghton Mifflin red.). New York: Dover Publications. s. 113–115. ISBN 978-0-486-46237-0 .
Wells D (1991). Penguin Dictionary of Curious and Interesting Geometry . New York: Penguin Books. s. 244–245 . ISBN 0-14-011813-6 .

Vidare läsning

Eves H (1972). A Survey of Geometry (reviderad utg.). Boston: Allyn och Bacon. s. 134–135. ISBN 978-0-205-03226-6 .
Pedoe D (1970). En kurs i geometri för högskolor och universitet . Cambridge University Press. s. 97–101. ISBN 978-0-521-07638-8 .
Coolidge JL (1916). En avhandling om cirkeln och sfären . Oxford: Clarendon Press. s. 31–37.

externa länkar

Weisstein, Eric W. "Steiner Chain" . MathWorld .
Interaktiv animering av en Steiner-kedja , CodePen
Interaktiv applet av Michael Borcherds som visar en animation av Steiners kedja med ett varierande antal cirklar gjorda med GeoGebra .