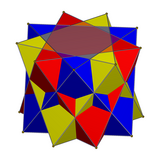
Sammansättning av tre oktaedrar
| Sammansättning av tre oktaedrar | |
|---|---|
|
|
| Polyedra | 3 vanliga oktaedrar |
| Ansikten | 24 liksidiga trianglar |
| Kanter | 36 |
| Vertices | 18 |
|
Symmetrigrupp (enfärgad) |
Åh , beställning 48 |
I matematik är sammansättningen av tre oktaedrar eller oktaeder 3-förening en polyedrisk sammansättning bildad av tre vanliga oktaedrar , alla delar ett gemensamt centrum men roterade i förhållande till varandra. Även om den förekom tidigare i den matematiska litteraturen, återupptäcktes den och populariserades av MC Escher , som använde den i den centrala bilden av hans 1948 träsnitt Stars .
Konstruktion
En vanlig oktaeder kan omskrivas runt en kub på ett sådant sätt att de åtta kanterna på två motsatta kvadrater av kuben ligger på oktaederns åtta ytor. De tre oktaedrarna som bildas på detta sätt från de tre paren av motsatta kubrutor bildar sammansättningen av tre oktaedrar. De åtta kubens hörn är desamma som de åtta punkterna i sammansättningen där tre kanter korsar varandra. Var och en av oktaederkanterna som deltar i dessa trippelkorsningar delas med korsningspunkten i förhållandet 1: √ 2 . De återstående oktaederkanterna korsar varandra i par, inom föreningens inre; deras korsningar är i deras mittpunkter och bildar räta vinklar.
Sammansättningen av tre oktaedrar kan också bildas av tre kopior av en enda oktaeder genom att vrida varje kopia med en vinkel på π /4 runt en av de tre symmetriaxlarna som passerar genom två motsatta hörn av startoktaedern. En tredje konstruktion för samma sammansättning av tre oktaedrar är som den dubbla polyhedronen av sammansättningen av tre kuber, en av de enhetliga polyhedronföreningarna .
De sex hörnen på en av de tre oktaedrarna kan ges av koordinaterna (0, 0, ±2) och (± √ 2 , ± √ 2 , 0) . De andra två oktaedrarna har koordinater som kan erhållas från dessa koordinater genom att byta ut z -koordinaten mot x- eller y -koordinaten.
Symmetrier

Sammansättningen av tre oktaedrar har samma symmetrigrupp som en enkel oktaeder. Det är en isohedral deltahedron , vilket betyder att dess ansikten är liksidiga trianglar och att den har en symmetri som tar varje ansikte till varannan ansikte. Det finns en känd oändlig familj av isoedriska deltaedrar, och 36 fler som inte tillhör denna familj; föreningen av tre oktaedrar är ett av de 36 sporadiska exemplen. Dess symmetrigrupp tar dock inte varje vertex till vartannat vertex, så det är inte i sig en enhetlig polyederförening.
Skärningen mellan de tre oktaedrarna är en konvex polyeder med 14 hörn och 24 ytor, en tetrakis-hexaeder , bildad genom att fästa en låg fyrkantig pyramid på varje yta av den centrala kuben. Således kan föreningen ses som en stellation av tetrakis-hexaedern. En annan form av tetrakis-hexaedern, bildad genom att använda högre pyramider på varje sida av kuben, är icke-konvex men har liksidiga triangelytor som återigen ligger på samma plan som ytorna på de tre oktaedrarna; det är en annan av de kända isoedriska deltahedrarna. En tredje isoedrisk deltahedron som delar samma vända plan, sammansättningen av sex tetraedrar , kan bildas genom att framställa varje sida av sammansättningen av tre oktaedrar för att bilda tre stellae octangulae . En fjärde isoedrisk deltaeder med samma ytplan, också en bild av sammansättningen av tre oktaedrar, har samma kombinatoriska struktur som tetrakis-hexaedern men med kubytorna buckliga inåt i korsande pyramider snarare än att fästa pyramiderna på kubens utsida .
Kuben runt vilken de tre oktaedrarna kan omskrivas har nio plan av reflektionssymmetri . Tre av dessa reflektionsrutor passerar parallellt med kubens sidor, halvvägs mellan två motsatta sidor; de andra sex passerar diagonalt över kuben, genom fyra av dess hörn. Dessa nio plan sammanfaller med de nio ekvatorialplanen i de tre oktaedrarna.
Historia
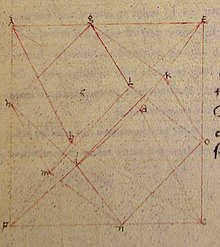
I 1400-talsmanuskriptet De quinque corporibus regularibus av Piero della Francesca innehåller della Francesca redan en teckning av en oktaeder omskriven runt en kub, med åtta av kubkanterna liggande i oktaederns åtta ytor. Tre oktaedrar omskrivna på detta sätt runt en enda kub skulle bilda sammansättningen av tre oktaedrar, men della Francesca avbildar inte sammansättningen.
Nästa framträdande av sammansättningen av tre oktaedrar i den matematiska litteraturen verkar vara ett verk från 1900 av Max Brückner , som nämner det och inkluderar ett fotografi av en modell av det.
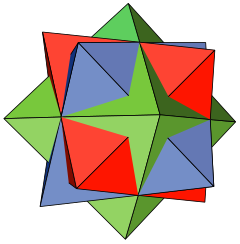
Den holländska konstnären MC Escher , i sitt träsnitt Stars från 1948 , använde som träsnittets centrala figur en bur i denna form, innehållande två kameleonter och svävande genom rymden. HSM Coxeter , antar att Escher återupptäckte denna form självständigt, skriver att "Det är anmärkningsvärt att Escher, utan någon kunskap om algebra eller analytisk geometri, kunde återupptäcka denna mycket symmetriska figur." George W. Hart har dock dokumenterat att Escher var bekant med Brückners arbete och använde det som grund för många av de stellerade polyedrarna och polyedriska föreningarna som han ritade. Tidigare 1948 hade Escher gjort ett preliminärt träsnitt med ett liknande tema, Study for Stars , men istället för att använda sammansättningen av tre vanliga oktaedrar i studien använde han en annan men besläktad form, en stjärnformad rombisk dodekaeder (ibland kallad Eschers solid) , som kan bildas som en förening av tre tillplattade oktaedrar. Denna form som en polyeder är topologiskt identisk med disdyakis dodecahedron , som kan ses som rombisk dodekaeder med kortare pyramider på de rombiska ytorna. Den dubbla figuren av den oktaedriska sammansättningen, sammansättningen av tre kuber, visas också i ett senare Escher-träsnitt, Vattenfall , bredvid samma stjärnformade rombiska dodekaeder.
Sammansättningen av tre oktaedrar återinträdde mer korrekt i den matematiska litteraturen med arbetet av Bakos & Johnson (1959), som observerade dess existens och gav koordinater för dess hörn. Den studerades mer i detalj av Wenninger (1968) och Coxeter (1985) .
Andra föreningar av tre oktaedrar
Med oktaedrarna sedda som triangulära antiprismor , finns en annan enhetlig prismatisk sammansättning av antiprismor med D 3d symmetri, ordning 12. Varje antiprisma roteras 40 grader. Det övre och nedre planet kan ses innehålla det sammansatta enneagrammet , {9/3} eller 3{3}.
Se även
- Sammansättning av fyra oktaedrar
- Sammansättning av fem oktaedrar
- Sammansättning av tio oktaedrar
- Sammansättning av tjugo oktaedrar