Rabi -frekvensen är den frekvens vid vilken sannolikhetsamplituderna för två atomenerginivåer fluktuerar i ett oscillerande elektromagnetiskt fält. Den är proportionell mot övergångsdipolmomentet för de två nivåerna och mot amplituden ( inte intensiteten ) hos det elektromagnetiska fältet . Befolkningsöverföring mellan nivåerna i ett sådant 2-nivåsystem upplyst med ljus som exakt resonerar med skillnaden i energi mellan de två nivåerna kommer att ske vid Rabi-frekvensen; när det infallande ljuset avstäms från denna energiskillnad (avstämt från resonans) så sker populationsöverföringen vid den generaliserade Rabi-frekvensen . Rabi-frekvensen är ett semiklassiskt begrepp eftersom det behandlar atomen som ett objekt med kvantiserade energinivåer och det elektromagnetiska fältet som en kontinuerlig våg.
I samband med ett kärnmagnetisk resonansexperiment är Rabi-frekvensen nutationsfrekvensen för ett provs nettokärnmagnetiseringsvektor kring ett radiofrekvent fält. (Observera att detta skiljer sig från Larmor-frekvensen , som kännetecknar precessionen av en tvärgående kärnmagnetisering kring ett statiskt magnetfält.)
Härledning
Betrakta två energiegentillstånd för ett kvantsystem med Hamiltonian  exempelvis kan detta vara Hamiltonian för en partikel i en
exempelvis kan detta vara Hamiltonian för en partikel i en  potential, som väteatomen eller alkaliatomerna):
potential, som väteatomen eller alkaliatomerna):

Vi vill överväga den tidsberoende Hamiltonian

där  är potentialen för det elektromagnetiska fältet. Om vi behandlar potentialen som en störning kan vi förvänta oss att egentillstånden för den störda Hamiltonianen är en blandning av egentillstånden för den ursprungliga Hamiltonianen med tidsberoende koefficienter:
är potentialen för det elektromagnetiska fältet. Om vi behandlar potentialen som en störning kan vi förvänta oss att egentillstånden för den störda Hamiltonianen är en blandning av egentillstånden för den ursprungliga Hamiltonianen med tidsberoende koefficienter:

Pluggar in detta i den tidsberoende Schrödinger-ekvationen

tar den inre produkten med var och en av  och
och 
 , och använder ortogonalitetsvillkoret för egentillstånd vi kommer fram till två ekvationer i koefficienterna
, och använder ortogonalitetsvillkoret för egentillstånd vi kommer fram till två ekvationer i koefficienterna  och
och  :
:

där  . De två termerna inom parentes är dipolmatriselement prickade in i det elektromagnetiska fältets polarisationsvektor. Vid betraktande av de sfäriskt symmetriska rumsliga egenfunktionerna
. De två termerna inom parentes är dipolmatriselement prickade in i det elektromagnetiska fältets polarisationsvektor. Vid betraktande av de sfäriskt symmetriska rumsliga egenfunktionerna  av väteatomens potential går de diagonala matriselementen till noll, vilket lämnar oss med
av väteatomens potential går de diagonala matriselementen till noll, vilket lämnar oss med

eller

Här  , där
, där  är Rabi-frekvensen.
är Rabi-frekvensen.
Intuition
I täljaren har vi övergångsdipolmomentet för i  -övergången, vars kvadratiska amplitud representerar styrkan av interaktionen mellan det elektromagnetiska fältet och atomen, och
-övergången, vars kvadratiska amplitud representerar styrkan av interaktionen mellan det elektromagnetiska fältet och atomen, och  är vektorns elektriska fältamplitud , som inkluderar polarisationen . Täljaren har dimensioner av energi, så att dividera med
är vektorns elektriska fältamplitud , som inkluderar polarisationen . Täljaren har dimensioner av energi, så att dividera med  ger en vinkelfrekvens .
ger en vinkelfrekvens .
I analogi med en klassisk dipol är det tydligt att en atom med ett stort dipolmoment kommer att vara mer mottagligt för störning av ett elektriskt fält. Punktprodukten inkluderar en faktor  \ , där
\ , där  är vinkeln mellan ljusets polarisation och övergångsdipolmomentet. När de är parallella är interaktionen starkast, när de är vinkelräta sker ingen interaktion alls.
är vinkeln mellan ljusets polarisation och övergångsdipolmomentet. När de är parallella är interaktionen starkast, när de är vinkelräta sker ingen interaktion alls.
Om vi skriver om differentialekvationerna ovan:

och tillämpa rotationsvågsapproximationen , som antar att  så att vi kan förkasta högfrekventa oscillerande termer, vi har
så att vi kan förkasta högfrekventa oscillerande termer, vi har

där  . Vi kan lösa dessa ekvationer, förutsatt att vid tidpunkten
. Vi kan lösa dessa ekvationer, förutsatt att vid tidpunkten  är atomen i
är atomen i  (dvs
(dvs  ) för att hitta
) för att hitta

Detta är sannolikheten som en funktion av avstämning och tid för befolkningen i staten  . En plot som funktion av avstämning och rampning av tiden från 0 till
. En plot som funktion av avstämning och rampning av tiden från 0 till  ger:
ger:
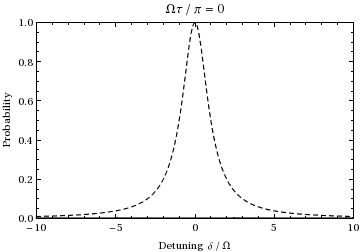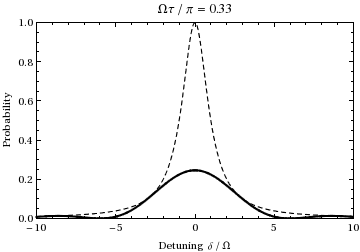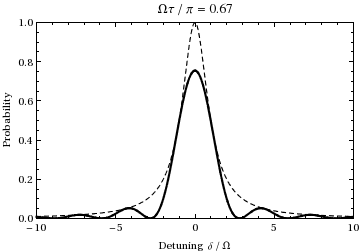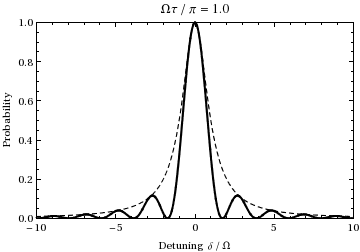
Vi ser att för  kommer populationen att pendla mellan de två tillstånden vid Rabi-frekvensen.
kommer populationen att pendla mellan de två tillstånden vid Rabi-frekvensen.
Generaliserad Rabi-frekvens
Kvantiteten  kallas vanligen för den "generaliserade Rabi-frekvensen." För fall där
kallas vanligen för den "generaliserade Rabi-frekvensen." För fall där  Rabi-floppning vid denna frekvens, där δ
Rabi-floppning vid denna frekvens, där δ  är avstämningen , ett mått på hur långt ljuset är off-resonans i förhållande till övergång. Om man till exempel undersöker ovanstående animation med en offsetfrekvens på ±1,73, kan man se att under den 1/2 Rabi-cykel (vid resonans) som visas under animeringen, genomgår svängningen istället en hel cykel, alltså vid dubbelt så mycket ( normalt ) Rabi-frekvens
är avstämningen , ett mått på hur långt ljuset är off-resonans i förhållande till övergång. Om man till exempel undersöker ovanstående animation med en offsetfrekvens på ±1,73, kan man se att under den 1/2 Rabi-cykel (vid resonans) som visas under animeringen, genomgår svängningen istället en hel cykel, alltså vid dubbelt så mycket ( normalt ) Rabi-frekvens  , precis som förutspått av denna ekvation. Observera också att när det infallande ljusets frekvens skiftar längre från övergångsfrekvensen, minskar amplituden för Rabi-svängningen, vilket illustreras av den streckade enveloppen i diagrammet ovan.
, precis som förutspått av denna ekvation. Observera också att när det infallande ljusets frekvens skiftar längre från övergångsfrekvensen, minskar amplituden för Rabi-svängningen, vilket illustreras av den streckade enveloppen i diagrammet ovan.
Två-foton Rabi-frekvens
Koherenta Rabi-svängningar kan också drivas av tvåfotonövergångar . I det här fallet betraktar vi ett system med tre atomenerginivåer,  ,
,  och
och  , där
, där  representerar ett så kallat mellantillstånd med motsvarande frekvens
representerar ett så kallat mellantillstånd med motsvarande frekvens  , och ett elektromagnetiskt fält med två frekvenskomponenter:
, och ett elektromagnetiskt fält med två frekvenskomponenter:

Nu kan  vara mycket större än både
vara mycket större än både  och
och  , eller
, eller  som illustreras i bilden till höger.
som illustreras i bilden till höger.

Två fotoner excitationsschema.

visas till vänster, medan

visas till höger. Den vertikala axeln är frekvensaxeln (eller energiaxeln).
En tvåfotonövergång är inte detsamma som excitation från marken till mellantillståndet, och sedan ut ur det mellanliggande tillståndet till det exciterade tillståndet. Istället absorberar atomen två fotoner samtidigt och främjas direkt mellan det initiala och slutliga tillståndet. Det finns två nödvändiga förutsättningar för att denna två-fotonprocess (även känd som en Raman-process), ska vara den dominerande modellen för ljus-materia-interaktionen:

Med ord måste summan av frekvenserna för de två fotonerna vara i resonans med övergången mellan initial- och sluttillståndet, och fotonernas individuella frekvenser måste avstämmas från mellantillståndet till initial- och sluttillståndsövergångarna. Om det sistnämnda villkoret inte är uppfyllt och  kommer den dominerande processen att styras av hastighetsekvationer där det mellanliggande tillståndet befolkas och stimuleras och spontana emissionshändelser från det tillståndet förhindrar möjligheten att driver koherenta svängningar mellan det initiala och slutliga tillståndet.
kommer den dominerande processen att styras av hastighetsekvationer där det mellanliggande tillståndet befolkas och stimuleras och spontana emissionshändelser från det tillståndet förhindrar möjligheten att driver koherenta svängningar mellan det initiala och slutliga tillståndet.
Vi kan härleda tvåfotonernas Rabi-frekvens genom att återgå till ekvationerna

som nu beskriver excitation mellan mark- och mellantillstånd. Vi vet att vi har lösningen

där  är den generaliserade Rabi-frekvensen för övergången från det initiala till det mellanliggande tillståndet. På samma sätt har vi ekvationerna för den mellanliggande till slutliga övergången
är den generaliserade Rabi-frekvensen för övergången från det initiala till det mellanliggande tillståndet. På samma sätt har vi ekvationerna för den mellanliggande till slutliga övergången

Nu kopplar vi in  i ekvationen ovan för
i ekvationen ovan för 

Så att när vi löser denna ekvation finner vi att koefficienten är proportionell mot:

Detta är den effektiva eller två-foton Rabi-frekvensen. Det är produkten av de individuella Rabi-frekvenserna för  och
och  övergångar, dividerat med avstämningen från det mellanliggande tillståndet
övergångar, dividerat med avstämningen från det mellanliggande tillståndet  .
.
Se även


























































