Multitrait-multimethod-matris

Multitrait -multimethod- matrisen ( MTMM ) är ett tillvägagångssätt för att undersöka konstruktionsvaliditet utvecklat av Campbell och Fiske (1959). Den organiserar konvergenta och diskriminerande giltighetsbevis för jämförelse av hur en åtgärd förhåller sig till andra åtgärder. Det konceptuella tillvägagångssättet har påverkat experimentell design och mätteori inom psykologi, inklusive tillämpningar i strukturella ekvationsmodeller.

Definitioner och nyckelkomponenter

Flera egenskaper används i detta tillvägagångssätt för att undersöka (a) liknande eller (b) olika egenskaper ( konstruktioner ), för att fastställa konvergent och diskriminerande giltighet mellan egenskaper. På liknande sätt används flera metoder i detta tillvägagångssätt för att undersöka de differentiella effekterna (eller avsaknaden av sådana) orsakade av metodspecifik varians. Poäng kan korreleras eftersom de mäter liknande egenskaper, eller för att de är baserade på liknande metoder, eller båda. När variabler som ska mäta olika konstruktioner visar en hög korrelation eftersom de bygger på liknande metoder, beskrivs detta ibland som ett problem med "olägenhetsvarians" eller "metodbias".

Det finns sex viktiga överväganden när man undersöker en konstruktions giltighet genom MTMM-matrisen, som är följande:

1. Utvärdering av konvergent validitet – Tester utformade för att mäta samma konstruktion bör korrelera starkt sinsemellan.
2. Utvärdering av diskriminant (divergent) validitet – Den konstruktion som mäts med ett test bör inte korrelera i hög grad med olika konstruktioner.
3. Egenskapsmetodenhet - Varje uppgift eller test som används för att mäta en konstruktion anses vara en egenskapsmetodenhet; genom att variansen i måttet är en del av egenskapen och en del av metoden. I allmänhet önskar forskare låg metodspecifik varians och hög egenskapsvarians.
4. Multitrait-multimethod – Mer än en egenskap och mer än en metod måste användas för att fastställa (a) diskriminant validitet och (b) de relativa bidragen från egenskapen eller metodspecifik varians. Denna grundsats överensstämmer med de idéer som föreslås i Platts koncept Strong inference (1964).
5. Verkligen olika metodik – När man använder flera metoder måste man överväga hur olika de faktiska åtgärderna är. Till exempel, att leverera två självrapporteringsmått är inte riktigt olika mått; medan en intervjuskala eller en psykosomatisk läsning skulle vara det.
6. Egenskaper – Egenskaper bör vara tillräckligt olika för att vara distinkta, men tillräckligt lika för att vara värda att undersöka i MTMM.

Exempel

Exemplet nedan ger en prototypisk matris och vad korrelationerna mellan mått betyder. Den diagonala linjen fylls vanligtvis i med en tillförlitlighetskoefficient för måttet (t.ex. alfakoefficient). Beskrivningar inom parentes [] indikerar vad som förväntas när validiteten av konstruktionen (t.ex. depression eller ångest) och validiteterna för måtten alla är höga.

Testa	Beck Depression Inventory (BDI) - Frågeformulär	Hamilton Depression Rating Scale (HDRS) - Intervju	Beck Anxiety Inventory (BAI) - Frågeformulär	Kliniker Globala intryck - Ångest (CGI-A) - Intervju
BDI	(Tillförlitlighetskoefficient) [nära 1.00]
HDRS	Heterometod-monotrait [högst av alla utom tillförlitlighet]	(Tillförlitlighetskoefficient) [nära 1.00]
BAI	Monometod-heterotrait [låg, mindre än monotrait]	Heterometod-heterotrait [lägst av alla]	(Tillförlitlighetskoefficient) [nära 1,00]
CGI-A	Heterometod-heterotrait [lägst av alla]	Monometod-heterotrait [låg, mindre än monotrait]	Heterometod-monotrait [högst av alla utom tillförlitlighet]	(Tillförlitlighetskoefficient) [nära 1.00]

I det här exemplet listar den första raden egenskapen som bedöms (dvs. depression eller ångest) samt metoden för att bedöma denna egenskap (dvs. självrapporterat frågeformulär kontra en intervju). Termen heterometod indikerar att denna cell rapporterar korrelationen mellan två separata metoder. Monometod indikerar att samma metod används istället (t.ex. intervju och intervju). Heterotrait indikerar att cellen refererar till två förmodat olika egenskaper. Monotrait indikerar samma egenskap som ska mätas.

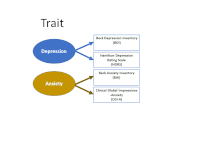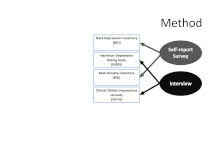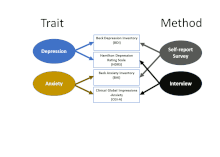
Detta ramverk gör det tydligt att det finns minst två källor till varians som kan påverka observerade poäng på ett mått: Inte bara den underliggande egenskapen (vilket vanligtvis är målet med att samla in mätningen i första hand), utan också metoden som används för att samla in måttet. MTMM-matrisen använder två eller flera mått på varje egenskap och två eller flera metoder för att börja riva isär bidragen från olika faktorer. Den första ramen i den animerade figuren visar hur de fyra måtten i tabellen är parade när det gäller att fokusera på "dragen" av depression (BDI och HDRS) och ångest (BAI och CGI-A). Den andra visar att de också är parade när det gäller källmetod: två använder självrapporteringsfrågeformulär (ofta kallade "enkäter"), och två är baserade på intervju (som också kan inkludera direkt observation av icke-verbal kommunikation och beteende, som intervjupersonens svar).

Poängen på varje mått påverkas av både egenskapen och även metoden med vilken informationen samlas in

Med observerade data är det möjligt att undersöka andelen varians som delas mellan egenskaper och metoder för att få en känsla av hur mycket metodspecifik varians som induceras av mätmetoden, samt ge en titt på hur distinkt egenskapen är, som jämfört med en annan egenskap.

Idealt sett borde egenskapen ha större betydelse än den specifika metod som valts för mätning. Till exempel, om en person mäts som mycket deprimerad av en åtgärd, bör en annan depressionsåtgärd också ge höga poäng. Å andra sidan bör personer som verkar mycket deprimerade på Becks depressionsinventering inte nödvändigtvis få höga ångestvärden på Becks ångestinventering, eftersom de är tänkta att mäta olika konstruktioner. Eftersom inventeringarna skrevs av samma person och har liknande stil, kan det finnas en viss korrelation, men denna likhet i metod bör inte påverka poängen särskilt mycket, så korrelationerna mellan dessa mått på olika egenskaper bör vara låga.

Analys

En mängd olika statistiska metoder har använts för att analysera data från MTMM-matrisen. Standardmetoden från Campbell och Fiske kan implementeras med programmet MTMM.EXE som finns tillgängligt på: https://web.archive.org/web/20160304173400/http://gim.med.ucla.edu/FacultyPages/Hays/utils / Man kan också använda bekräftande faktoranalys på grund av komplexiteten i att beakta all data i matrisen. Sawilowsky I-testet tar dock hänsyn till alla data i matrisen med ett distributionsfritt statistiskt test för trend.

Exempel på en MTMM-mätmodell

Testet genomförs genom att reducera trianglarna heterotrait-heterometod och heterotrait-monometod, samt validitets- och reliabilitetsdiagonalerna, till en matris med fyra nivåer. Varje nivå består av minimi-, median- och maximivärde. Nollhypotesen är att dessa värden är oordnade, vilket testas mot den alternativa hypotesen om en ökande ordnad trend. Teststatistiken hittas genom att räkna antalet inversioner (I). Det kritiska värdet för alfa = 0,05 är 10 och för alfa = 0,01 är 14.

En av de mest använda modellerna för att analysera MTMM-data är True Score-modellen som föreslagits av Saris och Andrews (). True Score-modellen kan uttryckas med hjälp av följande standardiserade ekvationer:

 
          1)   Y  ij  =  r  ij  TS  ij  +  e  ij  *  där:  Y  ij  är den standardiserade observerade variabeln mätt med den i:  te  egenskapen och den j:  te  metoden.  r  ij  är tillförlitlighetskoefficienten, som är lika med:  r  ij  =  σ  Y  ij  /  σ  TS  ij  TS  ij  är den standardiserade sanna poängvariabeln  e  ij  *  är det slumpmässiga felet, vilket är lika med:  e  ij  *  =  e  ij  /  σ  Y  ij  Följaktligen:   r  ij  2  =  1  -  σ  2  (e  ij  *)  där:  r  ij  2  är reliabiliteten 

 
         
          2)    TS  ij  =  v  ij  F  i  +  m  ij  M  j  där:  v  ij  är giltighetskoefficienten, vilket är lika med:  v  ij  =  σ  F  i  /  σ  TS  ij  F  i  är den standardiserade latenta faktorn för den i:  e  variabeln av intresse (eller egenskap)  m  ij  är metodeffekten, som är lika med:  m  ij  =  σ  M  j  /  σ  TS  ij  M  j  är den standardiserade latenta faktorn för reaktionen på den j:  te  metoden. Följaktligen:  v  ij  2  =  1  -  m  ij  2  där:  v  ij  2  är giltigheten 

 3)  Y  ij  =  q  ij  F  i  +  r  ij  m  ij  M  j  +  e*  där:  q  ij  är kvalitetskoefficienten, som är lika med:  q  ij  =  r  ij  •  v  ij  Följaktligen:  q  ij  2  =  r  ij  2  •  v  ij  2  =  σ  2  F  i  /  σ  2  Y  ij  där:  q  ij  2  är kvaliteten 

Antagandena är följande:

 * Felen är slumpmässiga, så medelvärdet av felen är noll:  µ  e  =  E  (e)  = 0  * De slumpmässiga felen är okorrelerade med varandra:  cov  (e  i  , e  j  )  =  E  (e  i  e  j  )  = 0  * De slumpmässiga felen är okorrelerade med de oberoende variablerna:  cov  (TS, e)  =  E  (TS e)  = 0  ,  cov  (F, e)  =  E  (F e)  = 0  och  cov  (M, e)  =  E  (M e)  = 0  * Metodfaktorerna antas vara okorrelerade med varandra och med egenskapsfaktorerna:  cov  (F, M)  =  E  (FM)  = 0 

Vanligtvis måste respondenten svara på minst tre olika mått (dvs. egenskaper) mätt med minst tre olika metoder. Denna modell har använts för att uppskatta kvaliteten på tusentals enkätfrågor, särskilt inom ramen för European Social Survey .