Metod för matchade asymptotiska expansioner

Inom matematiken är metoden för matchade asymptotiska expansioner ett vanligt tillvägagångssätt för att hitta en exakt approximation av lösningen på en ekvation eller ekvationssystem . Det används särskilt när man löser singulärt störda differentialekvationer . Det handlar om att hitta flera olika ungefärliga lösningar, som var och en är giltig (dvs korrekt) för en del av intervallet för den oberoende variabeln, och sedan kombinera dessa olika lösningar för att ge en enda ungefärlig lösning som är giltig för hela intervallet av värden av den oberoende variabeln. I den ryska litteraturen var dessa metoder kända under namnet "mellanliggande asymptotik" och introducerades i arbetet av Yakov Zeldovich och Grigory Barenblatt .

Metodöversikt

I en stor klass av enskilt störda problem kan domänen delas upp i två eller flera underdomäner. I en av dessa, ofta den största, approximeras lösningen exakt av en asymptotisk serie som hittas genom att problemet behandlas som en vanlig störning (dvs. genom att sätta en relativt liten parameter till noll). De andra underdomänerna består av ett eller flera små områden där den approximationen är inexakt, i allmänhet eftersom störningstermerna i problemet inte är försumbara där. Dessa områden kallas övergångsskikt och som gränsskikt eller inre skikt beroende på om de förekommer vid domängränsen (som är vanligt i applikationer) eller inne i domänen.

En approximation i form av en asymptotisk serie erhålls i övergångsskiktet/-en genom att behandla den delen av domänen som ett separat störningsproblem. Denna approximation kallas "den inre lösningen" och den andra är den "yttre lösningen", uppkallad efter deras förhållande till övergångsskiktet/-en. De yttre och inre lösningarna kombineras sedan genom en process som kallas "matchning" på ett sådant sätt att en ungefärlig lösning för hela domänen erhålls.

Ett enkelt exempel

Tänk på gränsvärdesproblemet

$$\varepsilon y''+(1+\varepsilon )y'+y=0,$$

där $y$ är en funktion av den oberoende tidsvariabeln $t$ , som sträcker sig från 0 till 1, är gränsvillkoren $y(0)=0$ och $y(1)=1$ , och $\varepsilon$ är en liten parameter, så att $0<\varepsilon \ll 1$ .

Yttre lösning, giltig för t = O (1)

Eftersom $\varepsilon$ är mycket liten, är vårt första tillvägagångssätt att behandla ekvationen som ett vanligt störningsproblem, dvs göra approximationen $\varepsilon =0$ , och därmed hitta lösningen på problemet

$$y'+y=0.$$

Tänk alternativt att när $y$ och $t$ båda är av storlek O (1), är de fyra termerna på vänster sida av den ursprungliga ekvationen respektive storleken $O(\varepsilon )$ , O (1), $O(\varepsilon )$ och O (1). Saldot i ledande ordning på denna tidsskala, giltigt i den distinguerade gränsen ${\displaystyle \varepsilon \to 0} ,$ ges därför av den andra och fjärde termen, dvs $y' +y=0.$

Detta har en lösning

$$y=Ae^{-t}$$

för någon konstant $A$ . Om vi ​​tillämpar gränsvillkoret $y(0)=0$ , skulle vi ha $A=0$ ; tillämpar gränsvillkoret $y(1)=1$ , skulle vi ha $A=e$ . Det är därför omöjligt att uppfylla båda gränsvillkoren, så $\varepsilon =0$ är inte en giltig uppskattning att göra över hela domänen (dvs detta är ett enskilt störningsproblem ). Av detta drar vi slutsatsen att det måste finnas ett gränsskikt vid en av ändpunkterna för domänen där $\varepsilon$ måste inkluderas. Denna region kommer att vara där $\varepsilon$ inte längre är försumbar jämfört med den oberoende variabeln $t$ , dvs. $t$ och $\varepsilon$ är av jämförbar storlek, dvs. gränsskiktet ligger intill $t=0$ . Därför gäller det andra gränsvillkoret $y(1)=1$ i detta yttre område, så $A=e$ , dvs ${\ displaystyle y_{\mathrm {O} }=e^{1-t}}$ är en exakt ungefärlig lösning på det ursprungliga gränsvärdesproblemet i detta yttre område. Det är den ledande lösningen.

Inre lösning, giltig för t = O ( ε )

I det inre området är $t$ och $\varepsilon$ båda små, men av jämförbar storlek, så definiera den nya O (1) tidsvariabeln $\tau =t /\varepsilon$ . Skala om det ursprungliga gränsvärdesproblemet genom att ersätta $t$ med $\tau \varepsilon$ , och problemet blir

$${\frac {1}{\varepsilon }}y''(\tau )+\ left({1+\varepsilon }\right){\frac {1}{\varepsilon }}y'(\tau )+y(\tau )=0,$$

som, efter att ha multiplicerat med $\varepsilon$ och tagit $\varepsilon =0$ , är

$$y''+y'=0.$$

Alternativt kan du tänka på att när $t$ har reducerats till storlek $O(\varepsilon )$ , så är $y$ fortfarande av storlek O (1) (med uttrycket för $y_{\mathrm {O} }$ ), och så de fyra termerna på vänster sida av den ursprungliga ekvationen har respektive storlek $O(\varepsilon ^{-1 })$ , $O(\varepsilon ^{-1})$ , O (1) och O (1). Saldot i ledande ordning på denna tidsskala, giltigt i den distinguerade gränsen ${\displaystyle \varepsilon \to 0} ,$ ges därför av den första och andra termen, dvs $y' '+y'=0.$

Detta har en lösning

$$y=B-Ce^{-\tau }$$

för vissa konstanter $B$ och $C$ . Eftersom $y(0)=0$ gäller i denna inre region, ger detta $B=C$ , så en exakt ungefärlig lösning på det ursprungliga gränsvärdesproblemet i denna inre region ( det är den ledande lösningen).

$$y_{\mathrm {I} }=B\left({1-e^{-\tau }}\right)=B\left({1-e^{-t/\varepsilon }}\right ).$$

Motsvarande

Vi använder matchning för att hitta värdet på konstanten $B$ . Tanken med matchning är att de inre och yttre lösningarna ska överensstämma för värden på $t$ i ett mellanliggande (eller överlappande) område, dvs där $\varepsilon \ll t\ll 1$ . Vi behöver den yttre gränsen för den inre lösningen för att matcha den inre gränsen för den yttre lösningen, dvs.

$$\lim _{\tau \to \infty }y_{\mathrm {I} }=\lim _{t\to 0}y_{\mathrm { O} },$$

vilket ger $B=e$ .

Ovanstående problem är det enklaste av de enkla problemen som hanterar matchade asymptotiska expansioner. Man kan omedelbart beräkna att $e^{1-t}$ är hela den asymptotiska serien för den yttre regionen medan ${\mathcal {O}}(\varepsilon )$ korrigering till den inre lösningen $y_{\mathrm {I} }$ är ${\textstyle B_{1}(1-e^{-t}) -{\underline {et}}}$ och konstanten för integration $B_{1}$ måste erhållas från inre-yttre matchning.

Lägg märke till den intuitiva idén för matchning att ta gränserna dvs ${\textstyle \lim _{\tau \to \infty }y_{\mathrm {I} }=\lim _{t\to 0}y_{\mathrm {O} },}$ gäller inte på denna nivå. Detta beror helt enkelt på att den understrukna termen inte konvergerar till en gräns. Metoderna att följa i dessa typer av fall är antingen att välja a) metoden för en intermediär variabel eller att använda b) Van-Dyke-matchningsregeln. Den förstnämnda metoden är besvärlig och fungerar alltid medan Van-Dyke matchningsregeln är lätt att implementera men med begränsad tillämplighet. Ett konkret gränsvärdesproblem med alla väsentliga ingredienser är följande.

Tänk på gränsvärdesproblemet

$$\varepsilon y''-x^{2}y'-y=1,\quad y(0) =y(1)=1$$

Den konventionella yttre expansionen $y_{\mathrm {O} }=y_{0}+\varepsilon y_{1}+\cdots$ ger ${\displaystyle y_{0}=\alpha e^{1/x}-1} ,$ där $\alpha$ måste erhållas från matchning.

Problemet har gränsskikt både till vänster och till höger. Det vänstra gränsskiktet nära $0$ har en tjocklek $\varepsilon ^{1/2}$ medan det högra gränsskiktet nära $1$ har tjockleken $\varepsilon$ . Låt oss först beräkna lösningen på det vänstra gränsskiktet genom att skala om ${\displaystyle X=x/\varepsilon ^{1/2},\;Y=y} ,$ sedan differentialekvation att uppfylla till vänster är

$$Y''-\varepsilon ^{1/2}X^{2}Y'-Y=1,\quad Y(0)=1$$

och följaktligen antar vi en expansion $Y^{l}=Y_{0}^{l}+\varepsilon ^{1/2} Y_{1/2}^{l}+\cdots$ .

O ${\mathcal {O}}(1)$ inhomogena tillstånd till vänster ger oss anledningen att starta expansionen vid $displaystyle {\mathcal {O}}(1) }$ . Den ledande ordningens lösning är $Y_{0}^{l}=2e^{-X}-1$ .

Detta med $1-1$ van-Dyke-matchning ger $\alpha =0$ .

Låt oss nu beräkna lösningen till höger omskalande ${\displaystyle X=(1-x)/\varepsilon ,\;Y=y} ,$ sedan differentialekvationen för att uppfylla till höger är

$$Y''+\left(1-2\varepsilon X+\varepsilon ^{ 2}X^{2}\right)Y'-\varepsilon Y=\varepsilon ,\quad Y(1)=1,$$

och därför antar vi en expansion

$$Y^{r}=Y_{0}^{r}+\varepsilon ^{1/2}Y_{1/2}^{r}+\cdots .$$

O ${\mathcal {O}}(1)$ inhomogena tillstånd till höger ger oss anledningen att starta expansionen vid $displaystyle {\mathcal {O}}(1) }$ . Den ledande ordningens lösning är $Y_{0}^{r}=(1-B)+Be^{-X}$ . Detta med $1-1$ van-Dyke-matchning ger $B=2$ . Om vi ​​går tillväga på liknande sätt om vi beräknar de högre ordningskorrigeringarna får vi lösningarna som

$$Y^{l}=2e^{-X}-1+\varepsilon ^{1/2}e^{-X}\left({\frac {X^{3}}{3}}+ {\frac {X^{2}}{2}}+{\frac {X}{2}}\right)+{\mathcal {O}}(\varepsilon ),\quad X={\frac {x }{\varepsilon ^{1/2}}}.$$

$$y\equiv -1.$$

$$Y^{r}=2e^{-X}-1+2\varepsilon e^{-X}\left(X+X^{2}\right)+{\mathcal {O}}(\ varepsilon ^{2}),\quad X={\frac {1-x}{\varepsilon }}.$$

Kompositlösning

För att erhålla vår slutliga, matchade, sammansatta lösning, giltig på hela domänen, är en populär metod den enhetliga metoden. I denna metod adderar vi de inre och yttre approximationerna och subtraherar deras överlappande värde, ${\displaystyle \,y_{\mathrm {överlapp} }} ,$ som annars skulle räknas två gånger. Det överlappande värdet är den yttre gränsen för den inre gränsskiktslösningen och den inre gränsen för den yttre lösningen; ovan befanns dessa gränser vara lika med $e$ . Därför är den slutliga ungefärliga lösningen på detta gränsvärdeproblem,

$$y(t)=y_{\mathrm {I} }+y_{\mathrm {O} }-y_{\mathrm {överlapp} }=e\left({1-e^{-t/\varepsilon }}\right)+e^{1-t}-e=e\left({e^{-t}-e^{-t/\varepsilon }}\right).$$

Observera att detta uttryck korrekt reduceras till uttrycken för $y_{\mathrm {I} }$ och $y_{\mathrm {O} }$ när $t$ är $O(\varepsilon )$ respektive O (1).

Noggrannhet

Konvergens av approximationer. Approximationer och exakta lösningar, som inte går att särskilja på denna skala, visas för olika $\varepsilon$ . Den yttre lösningen visas också. Observera att eftersom gränsskiktet blir smalare med minskande ${\displaystyle \varepsilon } ,$ konvergerar approximationerna till den yttre lösningen punktvis , men inte enhetligt , nästan överallt.

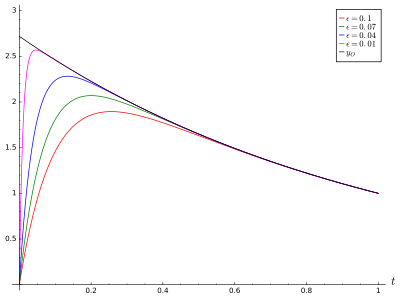
Denna slutliga lösning uppfyller problemets ursprungliga differentialekvation (visas genom att ersätta den och dess derivator i den ursprungliga ekvationen). Dessutom matchar gränsvillkoren som produceras av denna slutliga lösning de värden som ges i problemet, upp till en konstant multipel. Detta innebär, på grund av lösningens unika karaktär, att den matchade asymptotiska lösningen är identisk med den exakta lösningen upp till en konstant multipel. Detta är inte nödvändigtvis alltid fallet, alla återstående termer bör gå till noll jämnt som $\varepsilon \rightarrow 0$ .

Vår lösning löser inte bara det aktuella problemet på ett framgångsrikt sätt, den är nära problemets exakta lösning. Det händer att det här specifika problemet lätt kan hitta en exakt lösning

$$y(t)={\frac {e^{-t}-e^{-t/\ varepsilon }}{e^{-1}-e^{-1/\varepsilon }}},$$

som har samma form som den ungefärliga lösningen, med multiplikationskonstanten. Den ungefärliga lösningen är den första termen i en binomial expansion av den exakta lösningen i potenserna $e^{1-1/\varepsilon }$ .

Placering av gränsskikt

Bekvämt kan vi se att gränsskiktet, där $y'$ och $y''$ är stora, är nära $t=0$ , som vi antog tidigare. Om vi ​​hade antagit att det skulle vara vid den andra ändpunkten och gått vidare med att göra omskalningen ${\displaystyle \tau =(1-t)/\varepsilon } ,$ skulle vi ha funnit det omöjligt att uppfylla det resulterande matchningsvillkoret. För många problem är denna typ av försök och fel det enda sättet att bestämma den verkliga platsen för gränsskiktet.

Svårare problem

Problemet ovan är ett enkelt exempel eftersom det är en enda ekvation med bara en beroende variabel, och det finns ett gränsskikt i lösningen. Svårare problem kan innehålla flera medberoende variabler i ett system av flera ekvationer, och/eller med flera gräns- och/eller inre lager i lösningen.

Det är ofta önskvärt att hitta fler termer i de asymptotiska expansionerna av både de yttre och de inre lösningarna. Den lämpliga formen av dessa expansioner är inte alltid tydlig: medan en power-serie-expansion i $\varepsilon$ kan fungera, involverar den lämpliga formen ibland bråkpotenser av $\varepsilon$ , funktioner som $\varepsilon \log \varepsilon$ , et cetera. Som i exemplet ovan kommer vi att få yttre och inre expansioner med några koefficienter som måste bestämmas genom matchning.

Andra ordningens differentialekvationer

Schrödingerliknande differentialekvationer av andra ordningen

En metod för matchade asymptotiska expansioner - med matchning av lösningar i den gemensamma validitetsdomänen - har utvecklats och använts i stor utsträckning av Dingle och Müller-Kirsten för härledning av asymptotiska expansioner av lösningarna och karakteristiska tal (bandgränser) för Schrödinger-liknande andra ordningens differentialekvationer med periodiska potentialer - i synnerhet för Mathieu-ekvationen (bästa exemplet), Lamé- och ellipsoidala vågekvationer, oblate och prolate sfäroidala vågekvationer och ekvationer med anharmoniska potentialer.

Konvektion-diffusionsekvationer

Metoder för matchade asymptotiska expansioner har utvecklats för att hitta ungefärliga lösningar på Smoluchowskis konvektions-diffusionsekvation, som är en enskilt störd differentialekvation av andra ordningen. Problemet har studerats särskilt i samband med kolloida partiklar i linjära flödesfält, där variabeln ges av parfördelningsfunktionen runt en testpartikel. I gränsen för lågt Péclet-tal konvektions-diffusionsekvationen också en singularitet på oändligt avstånd (där normalt fjärrfältets gränsvillkor bör placeras) på grund av att flödesfältet är linjärt i separationen mellan partiklar. Detta problem kan kringgås med en rumslig Fouriertransform som visas av Jan Dhont. Ett annat tillvägagångssätt för att lösa detta problem utvecklades av Alessio Zaccone och medarbetare och består i att placera gränsvillkoret precis vid gränsskiktsavståndet, efter att anta (i en första ordningens approximation) ett konstant värde på parfördelningsfunktionen i det yttre skiktet på grund av att konvektion är dominerande där. Detta leder till en ungefärlig teori för möteshastigheten för två interagerande kolloidpartiklar i ett linjärt flödesfält i god överensstämmelse med den fullständiga numeriska lösningen. När Péclet-talet är betydligt större än ett, uppstår inte längre singulariteten vid oändlig separation och metoden för matchade asymptotik kan tillämpas för att konstruera den fullständiga lösningen för parfördelningsfunktionen över hela domänen.

Se även

• Asymptotisk analys
• Flerskalig analys
• Aktiveringsenergi asymptotik