Ljusets vinkelmoment

Ljusets totala rörelsemängd består av två komponenter, som båda verkar på olika sätt på en massiv kolloidal partikel som förs in i strålen. Spinnkomponenten får partikeln att snurra runt sin axel, medan den andra komponenten, känd som orbital angular momentum (OAM), får partikeln att rotera runt strålens axel.

Ljusets vinkelmoment är en vektormängd som uttrycker mängden dynamisk rotation som finns i ljusets elektromagnetiska fält . Medan den färdas ungefär i en rak linje kan en ljusstråle också rotera (eller " snurra " eller " snurra sig " ) runt sin egen axel. Denna rotation, även om den inte är synlig för blotta ögat , kan avslöjas genom interaktionen mellan ljusstrålen och materia.

Det finns två distinkta former av rotation av en ljusstråle, den ena involverar dess polarisering och den andra dess vågfrontsform . Dessa två former av rotation är därför associerade med två distinkta former av rörelsemängd , respektive benämnt ljus snurrande rörelsemängd (SAM) och lätt omloppsrörelsemängd (OAM).

Det totala vinkelmomentet för ljus (eller, mer allmänt, av det elektromagnetiska fältet och de andra kraftfälten ) och materia bevaras i tiden.

Introduktion

Ljus, eller mer allmänt en elektromagnetisk våg , bär inte bara energi utan också rörelsemängd , vilket är en karakteristisk egenskap hos alla objekt i translationsrörelse . Förekomsten av denna rörelsemängd blir uppenbar i fenomenet " strålningstryck " , där en ljusstråle överför sin rörelsemängd till ett absorberande eller spridande föremål och genererar ett mekaniskt tryck på det i processen.

Ljus kan också bära rörelsemängd , vilket är en egenskap hos alla föremål i roterande rörelse. Till exempel kan en ljusstråle rotera runt sin egen axel medan den fortplantar sig framåt. Återigen kan förekomsten av detta vinkelmoment göras uppenbart genom att överföra det till små absorberande eller spridande partiklar, som således utsätts för ett optiskt vridmoment.

För en ljusstråle kan man vanligtvis urskilja två " former av rotation " , den första associerad med den dynamiska rotationen av de elektriska och magnetiska fälten runt utbredningsriktningen, och den andra med den dynamiska rotationen av ljusstrålar runt huvudstrålens axel. Dessa två rotationer är associerade med två former av vinkelmoment , nämligen SAM och OAM. Denna distinktion blir emellertid suddig för starkt fokuserade eller divergerande strålar, och i det allmänna fallet kan endast det totala vinkelmomentet för ett ljusfält definieras. Ett viktigt begränsningsfall där distinktionen istället är tydlig och entydig är den för en " paraxiell " ljusstråle, det vill säga en väl kollimerad stråle där alla ljusstrålar (eller, mer exakt, alla Fourier - komponenter i det optiska fältet ) bara bildas små vinklar med strålaxeln .

För en sådan stråle är SAM strikt relaterad till den optiska polarisationen , och i synnerhet med den så kallade cirkulära polarisationen . OAM är relaterat till den rumsliga fältfördelningen, och i synnerhet med vågfrontens spiralform.

Utöver dessa två termer, om ursprunget för koordinaterna är beläget utanför strålens axel, finns det ett tredje rörelsemängdsbidrag som erhålls som tvärprodukten av strålens position och dess totala rörelsemängd . Denna tredje term kallas också " orbital " , eftersom den beror på fältets rumsliga fördelning. Men eftersom dess värde är beroende av valet av ursprung, kallas det " extern " orbital vinkelmomentum , i motsats till den " interna " OAM som uppträder för spiralformade strålar.

Matematiska uttryck för ljusets rörelsemängd

Ett vanligt använt uttryck för det totala rörelsemängdsmängden för ett elektromagnetiskt fält är följande, där det inte finns någon explicit skillnad mellan de två formerna av rotation:

$$\mathbf {J} =\varepsilon _{0}\int \mathbf {r} \times \left(\mathbf {E} \times \ mathbf {B} \right)d^{3}\mathbf {r} ,$$

där $\mathbf {E}$ och $\mathbf {B}$ är de elektriska respektive magnetiska fälten, $\epsilon _{0}$ är vakuumpermittiviteten och vi använder SI-enheter.

Ett annat uttryck för vinkelmomentet som naturligt härrör från Noethers sats är det följande, där det finns två separata termer som kan associeras med SAM ( ${\displaystyle \mathbf {S} } )$ och OAM ( $\mathbf {L}$ ):

$$\mathbf {J} =\varepsilon _{0}\int \left(\mathbf {E} \times \mathbf {A} \right)d^{3}\mathbf {r} +\varepsilon _{0}\sum _{i= x,y,z}\int \left(E^{i}\left(\mathbf {r} \times {\boldsymbol {\nabla }}\right)A^{i}\right)d^{3} \mathbf {r} =\mathbf {S} +\mathbf {L} ,$$

där $\mathbf {A}$ är vektorpotentialen för magnetfältet, och de i -överskrivna symbolerna betecknar de kartesiska komponenterna i motsvarande vektorer.

Dessa två uttryck kan bevisas vara likvärdiga med varandra för alla elektromagnetiska fält som försvinner tillräckligt snabbt utanför ett ändligt område av rymden. De två termerna i det andra uttrycket är dock fysiskt tvetydiga, eftersom de inte är mätinvarianta . En mätinvariant version kan erhållas genom att ersätta vektorpotentialen A och det elektriska fältet E med deras "tvärgående" eller radiativa komponent $\mathbf {A} _{\perp }$ och $\ mathbf {E} _{\perp }$ , vilket får följande uttryck:

$$\mathbf {J} _{\perp }=\varepsilon _{0}\int \left(\mathbf {E} _{\perp }\times \mathbf {A} _{\perp }\right) d^{3}\mathbf {r} +\varepsilon _{0}\sum _{i=x,y}\int \left({E^{i}}_{\perp}\left(\mathbf { r} \times {\boldsymbol {\nabla }}\right)A_{\perp }^{i}\right)d^{3}\mathbf {r} .$$

En motivering för att ta detta steg har ännu inte lämnats. Det senare uttrycket har ytterligare problem, eftersom det kan visas att de två termerna inte är sanna vinkelmoment eftersom de inte följer de korrekta kvantkommuteringsreglerna. Deras summa, det vill säga den totala rörelsemängden, gör det istället.

Ett ekvivalent men enklare uttryck för en monokromatisk våg med frekvens ω, med användning av den komplexa notationen för fälten, är följande:

$$\mathbf {J} ={\frac {\varepsilon _{0}}{2i\omega }}\int \left(\mathbf {E} ^{\ast }\times \mathbf {E} \right )d^{3}\mathbf {r} +{\frac {\varepsilon _{0}}{2i\omega }}\summa _{i=x,y,z}\int \left({E^{ i}}^{\ast }\left(\mathbf {r} \times {\boldsymbol {\nabla }}\right)E^{i}\right)d^{3}\mathbf {r} .$$

Låt oss nu betrakta den paraxiella gränsen, där strålaxeln antas sammanfalla med koordinatsystemets z-axel. I denna gräns är den enda signifikanta komponenten av rörelsemängden z ettan, det vill säga rörelsemängden som mäter ljusstrålens rotation runt sin egen axel, medan de andra två komponenterna är försumbara.

$$\mathbf {J} \approx {\frac {{\hat {z}}\epsilon _{0}}{2\omega }}\int \left(\left|E_{\text{L}} \right|^{2}-\left|E_{\text{R}}\right|^{2}\right)d^{3}\mathbf {r} +{\frac {{\hat {z} }\varepsilon _{0}}{2i\omega }}\int \sum _{i=x,y,z}\left({E^{i}}^{\ast }{\frac {\partial } {\partial \phi }}E^{i}\right)d^{3}\mathbf {r} .$$

där $E_{\text{L}}$ och $E_{\text{R}}$ betecknar de vänstra respektive högra cirkulära polarisationskomponenterna.

Utbyte av spinn och omloppsrörelsemängd med materia

Spinn och orbital rörelsemängd interaktion med materia

När en ljusstråle som bär rörelsemängd som inte är noll träffar en absorberande partikel, kan dess rörelsemängd överföras till partikeln, och på så sätt sätta den i roterande rörelse. Detta sker både med SAM och OAM. Men om partikeln inte är i strålens centrum kommer de två vinkelmomenten att ge upphov till olika typer av rotation av partikeln. SAM kommer att ge upphov till en rotation av partikeln runt sitt eget centrum, dvs till att en partikel snurrar. OAM kommer istället att generera ett varv av partikeln runt strålens axel. Dessa fenomen illustreras schematiskt i figuren.

I fallet med transparenta medier, i den paraxiella gränsen, byts den optiska SAM huvudsakligen ut mot anisotropa system, till exempel dubbelbrytande kristaller. Faktum är att tunna skivor av dubbelbrytande kristaller används vanligtvis för att manipulera ljuspolariseringen. Närhelst polarisationsellipticiteten ändras sker i processen ett utbyte av SAM mellan ljus och kristallen. Om kristallen är fri att rotera kommer den att göra det. Annars överförs SAM slutligen till hållaren och till jorden.

Spiral Phase Plate (SPP)

Schematisk för generering av lätt omloppsrörelsemängd med spiralfasplatta.

I den paraxiella gränsen kan OAM för en ljusstråle bytas ut mot materialmedia som har en transversell rumslig inhomogenitet. Till exempel kan en ljusstråle förvärva OAM genom att korsa en spiralfasplatta, med en inhomogen tjocklek (se figur).

Pitch-Fork hologram

Schematisk som visar generering av orbital vinkelmoment av ljus i en Gaussisk stråle.

Ett mer bekvämt tillvägagångssätt för att generera OAM är baserat på att använda diffraktion på ett gaffelliknande eller höggaffelhologram (se figur). Hologram kan också genereras dynamiskt under kontroll av en dator genom att använda en rumslig ljusmodulator .

Q-Plate

Q-plate-effekten för vänster och höger cirkulära polariseringar.

En annan metod för att generera OAM är baserad på SAM-OAM-kopplingen som kan förekomma i ett medium som är både anisotropt och inhomogent. I synnerhet är den så kallade q-plattan en enhet som för närvarande realiseras med hjälp av flytande kristaller, polymerer eller gitter med subvåglängd, som kan generera OAM genom att utnyttja en SAM-teckenförändring. I detta fall styrs OAM-tecknet av ingångspolarisationen.

Cylindriska lägesomvandlare

pi/2-cylindrisk lägesomvandlare förvandlar HG-läge till ett riktigt LG-läge.

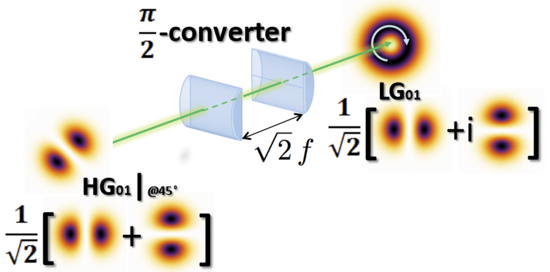
OAM kan också genereras genom att konvertera en Hermite-Gaussisk stråle till en Laguerre-Gaussian genom att använda ett astigmatiskt system med två väljusterade cylindriska linser placerade på ett specifikt avstånd (se figur) för att introducera en väldefinierad relativ fas mellan horisontella och vertikala Hermite-Gaussiska balkar.

Möjliga tillämpningar av ljusets orbitala vinkelmoment

Tillämpningarna av ljusets spinnvinkelmoment är oskiljbara från de otaliga tillämpningarna av ljuspolarisationen och kommer inte att diskuteras här. De möjliga tillämpningarna av ljusets omloppsrörelsemängd är istället för närvarande föremål för forskning. I synnerhet har följande applikationer redan demonstrerats i forskningslaboratorier, även om de ännu inte har nått kommersialiseringsstadiet:

1. Orienterande manipulation av partiklar eller partikelaggregat i optisk pincett
2. Informationskodning med hög bandbredd i optisk kommunikation med fritt utrymme
3. Högdimensionell kvantinformationskodning, för möjlig framtida kvantkryptografi eller kvantberäkningstillämpningar
4. Känslig optisk detektering

Se även

• Vinkelmoment
• Cirkulär polarisering
• Elektromagnetisk våg
• Helmholtz ekvation
• Ljus
• Lätt omloppsrörelsemängd
• Lätt snurr vinkelmoment
• Optiska virvlar
• Orbital vinkelmomentmultiplexering
• Polarisering (vågor)
• Fotonpolarisering

externa länkar

• Phorbitech
• Glasgow Optics Group
• Leiden Institute of Physics
• ICFO
• Università Di Napoli "Federico II" Arkiverad 2016-03-04 på Wayback Machine
• Università Di Roma "La Sapienza"
• Universitetet i Ottawa

Vidare läsning

•   Allen, L.; Barnett, Stephen M. & Padgett, Miles J. (2003). Optiskt vinkelmoment . Bristol: Institute of Physics. ISBN 978-0-7503-0901-1 .
•   Torres, Juan P. & Torner, Lluis (2011). Twisted Photons: Applikationer av ljus med orbital vinkelmoment . Bristol: Wiley-VCH. ISBN 978-3-527-40907-5 .
•   Andrews, David L. & Babiker, Mohamed (2012). Ljusets vinkelmoment . Cambridge: Cambridge University Press. sid. 448. ISBN 978-1-107-00634-8 .