Hilbert kub

Ej att förväxla med Hilbert-kurva .

Inom matematiken är Hilbertkuben, uppkallad efter David Hilbert , ett topologiskt utrymme som ger ett lärorikt exempel på några idéer inom topologi . Dessutom kan många intressanta topologiska utrymmen bäddas in i Hilbertkuben; det vill säga kan ses som delrum till Hilbertkuben (se nedan).

Definition

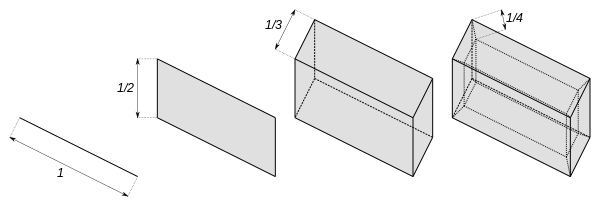
Hilbertkuben definieras bäst som den topologiska produkten av intervallen $[0,1/n]$ för $n=1,2,3,4,\ldots .$ Det vill säga, det är en kuboid med oändlig dimension , där längderna på kanterna i varje ortogonal riktning bildar sekvensen $\lbrace 1/n\rbrace _{n\in \mathbb {N} }.$

Hilbertkuben är homeomorf till produkten av otaliga oändligt många kopior av enhetsintervallet $[0,1].$ Med andra ord är den topologiskt omöjlig att skilja från enhetskuben med en oändlig dimension. Vissa författare använder termen "Hilbert-kub" för att betyda denna kartesiska produkt istället för produkten av $\left[0,{\tfrac {1}{n}}\right]$ .

Om en punkt i Hilbertkuben anges av en sekvens $\lbrace a_{n}\rbrace$ med $0\leq a_{n}\leq 1 /n,$ då ges en homeomorfism till den oändliga dimensionella enhetskuben av $h(a)_{n}=n\cdot a_{n}.$

Hilbertkuben som ett metriskt utrymme

Det är ibland bekvämt att tänka på Hilbert-kuben som ett metriskt utrymme , faktiskt som en specifik delmängd av ett separerbart Hilbert-utrymme (det vill säga ett Hilbert-utrymme med en countably oändlig Hilbert-bas). För dessa ändamål är det bäst att inte tänka på det som en produkt av kopior av $[0,1],$ utan istället som

$$[0,1]\ gånger [0,1/2]\ gånger [0,1/3]\ gånger \cdots ;$$

som nämnts ovan, för topologiska egenskaper, gör detta ingen skillnad. Det vill säga, ett element i Hilbertkuben är en oändlig sekvens

$$\left(x_{n}\right)$$

som tillfredsställer

$$0\leq x_{n}\leq 1/n.$$

Varje sådan sekvens tillhör Hilbert-utrymmet $\ell _{2},$ så Hilbert-kuben ärver ett mått därifrån. Man kan visa att topologin som induceras av metriken är densamma som produkttopologin i definitionen ovan.

Egenskaper

Som en produkt av kompakta Hausdorff - utrymmen är Hilbertkuben i sig ett kompakt Hausdorff - utrymme som ett resultat av Tychonoffs sats . Hilbertkubens kompakthet kan också bevisas utan valets Axiom genom att konstruera en kontinuerlig funktion från den vanliga Cantor-uppsättningen på Hilbertkuben.

I $\ell _{2},$ har ingen punkt en kompakt grannskap (därmed är $\ell _{2}$ inte lokalt kompakt ). Man kan förvänta sig att alla de kompakta delmängderna av $\ell _{2}$ är ändliga dimensionella. Hilbertkuben visar att så inte är fallet. Men Hilbertkuben misslyckas med att vara en grannskap av någon punkt $p$ eftersom dess sida blir mindre och mindre i varje dimension, så att en öppen boll runt $p$ med vilken fast radie som helst $e>0$ måste gå utanför kuben i någon dimension.

Varje oändligt dimensionell konvex kompakt delmängd av $\ell _{2}$ är homeomorf till Hilbertkuben. Hilbertkuben är en konvex uppsättning, vars spännvidd är hela utrymmet, men vars inre är tomt. Denna situation är omöjlig i ändliga dimensioner. Tangentkonen till kuben vid nollvektorn är hela rymden.

Varje delmängd av Hilbert-kuben ärver från Hilbert-kuben egenskaperna att vara både mätbar (och därför T4 ) och andra räkningsbar . Det är mer intressant att det omvända också gäller: vartannat räknebart T4 -utrymme är homeomorft till en delmängd av Hilbertkuben.

Varje G _δ -delmängd av Hilbert-kuben är ett polskt utrymme , ett topologiskt utrymme homeomorft till ett separerbart och komplett metriskt utrymme. Omvänt är varje polskt utrymme homeomorft till en G _δ -delmängd av Hilbertkuben.

Se även

• Lista över topologier – Lista över konkreta topologier och topologiska rum

Anteckningar

• Friedman, Harvey (1981). "Om nödvändig användning av abstrakt mängdteori" (PDF) . Framsteg i matematik . 41 (3): 209–280. doi : 10.1016/0001-8708(81)90021-9 . Hämtad 19 december 2022 .
•   Srivastava, Shashi Mohan (1998). En kurs i Borel-set . Graduate Texts in Mathematics . Springer-Verlag . ISBN 978-0-387-98412-4 . Hämtad 2008-12-04 .
• "Die Homoiomorphie der kompakten konvexen Mengen im Hilbertschen Raum" [De kompakta konvexa uppsättningarnas homomorfism i Hilberts rymd] (på tyska). EUDML. Arkiverad från originalet 2020-03-02.

Vidare läsning

•    Steen, Lynn Arthur ; Seebach, J. Arthur Jr. (1995) [1978]. Counterexamples in Topology ( Dover reprint of 1978 ed.). Berlin, New York: Springer-Verlag . ISBN 978-0-486-68735-3 . MR 0507446 .