Slutavslutningar för bildfilter

Filter designade med hjälp av bildimpedansmetodologin lider av en speciell brist i teorin. Filtrets förutsagda egenskaper beräknas under antagande att filtret avslutas med sina egna bildimpedanser i varje ände. Detta kommer vanligtvis inte att vara fallet; filtret kommer att avslutas med fasta motstånd. Detta gör att filtersvaret avviker från det teoretiska. Den här artikeln förklarar hur effekterna av slutavslutningar av bildfilter kan beaktas.

Generellt är effekten av avslutningarna att orsaka en avrundning av frekvenssvaret vid cut-off. Bildmetoden förutsäger en skarp diskontinuitet i lutningen av svaret vid cut-off vilket inte realiseras i praktiken, även om ett väldesignat bildfilter kan komma nära detta. En annan förutsägelse av bildmetoden är noll förlust i passbandet (under antagande av ideala förlustfria komponenter). Återigen, detta kan inte uppnås i praktiken eftersom reflektioner från slutavslut alltid orsakar en viss förlust.

Delar av denna artikel eller avsnitt förlitar sig på läsarens kunskap om den komplexa impedansrepresentationen av kondensatorer och induktorer och på kunskap om frekvensdomänrepresentationen av signaler .

Symboler som används i den här artikeln

Impedanser

• $\displaystyle Z_{I1}\,\!}$ { bildimpedansen i slutet 1
• $Z_{I2}\,\!$ bildimpedansen i slutet 2
• $Z_{I}\,\!$ bildimpedansen när båda ändarna är identiska
• $R_{1}\,\!$ det avslutande motståndet vid ände 1
• $R_{2}\,\!$ det avslutande motståndet vid ände 2
• $R\,\!$ det avslutande motståndet när båda ändarna är identiska

Koefficienter

• $\displaystyle r_{I1}\,\!}$ { reflektionskoefficienten i slutet 1
• $r_{I2}\,\!$ reflektionskoefficienten i slutet 2
• $r_{I}\,\!$ reflektionskoefficienten när båda ändarna är identiska
• $\displaystyle \tau _{I1}\,\!}$ { transmissionskoefficienten vid slutet 1
• $\tau _{I2}\,\!$ transmissionskoefficienten vid slutet 2
• $\gamma \,\!$ den komplexa utbredningskoefficienten för filtret
• $\alpha \,\!$ dämpningskoefficienten för filtret
• ${\displaystyle \beta \,\!$ } filtrets faskoefficient

Observera att alla dessa koefficienter är definierade i förhållande till bildimpedansen och inte den faktiska ingångsimpedansen för filtret.

Allmänt fall

Ett godtyckligt bildfilter med resistiva ändavslutningar. Eftersom avslutningarna inte ZI2 _är bildimpedansen är ingångs- och utgångsimpedansen inte ZI1 _. och , inte heller är inspänningen _faktiskt Vi

Överföringsfunktionen för ett filter som är anslutet som visas i diagrammet ovan ges av uttrycket

$A(i\omega )= {\frac {V_{o}}{V_{i}}}={\sqrt {\frac {Z_{I2}}{Z_{I1}}}}e^{-\gamma }\left[{\frac {\tau _{I1}\tau _{I2}}{1-e^{-2\gamma }r_{I1}r_{I2}}}\right]$

var

$r_{I1}={\frac {R_{1}-Z_{I1}}{R_{1}+Z_{I1}}}$

$r_{I2}={\frac {R_{2}-Z_{I2}}{R_{2}+Z_{I2}} }$

$\tau _{I1}={\frac {2Z_{I1}}{R_{1}+Z_{I1}}}$

$\tau _{I2}={\frac {2R_{2}}{R_{2}+Z_{I2}}}$

Observera att V _i är den nominella spänningen som skulle levereras av generatorn om den avslutades i sin karakteristiska impedans (dvs R ₁ ), inte den faktiska spänningen som uppträder vid filtrets ingångsterminaler.

Det kan vidare noteras att den första delen av uttrycket,

${\sqrt {\frac {Z_{I2}}{Z_{I1}}}}e^{-\gamma }$ ,

är detsamma som uttrycket för överföringsfunktionen utan att ta hänsyn till slutavslutningarna. Den andra delen av uttrycket är alltså den del av svaret som orsakas av de felaktiga impedanserna;

$\left[{\frac {\tau _{I1}\tau _{I2}}{1-e^{-2\gamma }r_{I1}r_{I2}}}\höger].$

Symmetriskt hölje

Där filtret har symmetriska bildimpedanser och avslutningar kan uttrycket reduceras avsevärt. Observera att det inte finns något krav på att filtret ska vara symmetriskt internt, bara att ändsektionerna har samma bildimpedans vänd mot identiska avslutningsimpedanser.

$A(i\omega )=e^{-\gamma }\left[{\frac {4Z_{I}R}{(R+Z_{I})^{2}-e^{-2\gamma }(R-Z_{I})^{2}}} \höger]$

En ytterligare förenkling kan göras om det inte finns några resistiva förluster i filtret (eller de antas vara försumbara). I detta iXI _fall är bildimpedansen rent reell ( RI ₎ i passbandet och rent imaginär ( ) i stoppbandet. Storleken på överföringsfunktionen ges av

$\left|A\right|={\frac {1}{\sqrt {1+\xi ^{2}}}}$

var för passbandet,

$\xi ={\frac {1}{2}}\left({\frac {R_{I}}{R}}-{ \frac {R}{R_{I}}}\right)\sin \beta$

och för stoppbandet,

$\xi ={\frac {1}{2}}\left({\frac {X_{I}}{R}}-{\frac {R}{X_{I}}}\right)\ sinh \beta .$

Antimetriskt fodral

En liknande förenkling kan göras för förlustfria antimetriska filter. I det här fallet substitutionen

$Z_{I1}Z_{I2}=R_{1}R_{2}=R_{o}^{2}$

görs till den allmänna ekvationen. För passbandet,

$\xi ={\frac {1}{2}}\left({\frac {R_{I1}}{R}}-{\frac {R}{R_{I1}}}\right)\ cos \beta .$

och för stoppbandet,

$\xi ={\frac {1}{2}}\left({\frac {X_{I1}}{R}}-{\frac {R}{X_{I1}}}\right)\ sinh \beta .$

Antimetrisk betyder i detta sammanhang att filterbildens impedanser och avslutningar i varje ände är dubbla av varandra. Detta kommer att vara fallet om filtret har en serie respektive shuntsektion av samma typ i varje ände. Symmetriska filter har ett jämnt antal halvsektioner och antimetriska filter har ett udda antal halvsektioner. I de allra flesta fall kommer filterdesignen att vara antingen symmetrisk eller antimetrisk och ett av dessa reducerade uttryck kommer att gälla.

Några exempel på svarsdiagram

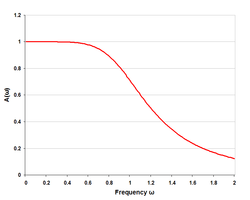
Teoretisk respons av ett korrekt avslutat lågpass prototyp T-filter	Svar från ett lågpassprototyp T-filter med hänsyn till effekten av resistiva ändavslutningar
Svaret från samma T-filter med det teoretiska svaret borttaget. Det vill säga komponenten i svaret beror endast på effekterna av slutavslutningarna.

Se även

• Bildimpedans
• Sammansatt bildfilter
• Dubbel impedans
• Prototypfilter
• Kategori:Bildimpedansfilter

• Matthaei, Young, Jones Microwave Filters, Impedance-Matching Networks, and Coupling Structures , s. 68-72, McGraw-Hill 1964.