Flerarmad bandit

En rad spelautomater i Las Vegas

Inom sannolikhetsteori och maskininlärning är det flerarmade banditproblemet (ibland kallat K- eller N -armat banditproblem ) ett problem där en fast begränsad uppsättning resurser måste allokeras mellan konkurrerande (alternativa) val på ett sätt som maximerar deras förväntade vinst, när varje vals egenskaper endast är delvis kända vid tilldelningstillfället, och kan bli bättre förstådda med tiden eller genom att allokera resurser till valet. Detta är ett klassiskt förstärkningsinlärningsproblem som exemplifierar dilemmat mellan utforskning och exploatering. Namnet kommer från att föreställa sig en spelare vid en rad spelautomater (ibland känd som " enarmade banditer "), som måste bestämma vilka maskiner som ska spelas, hur många gånger de ska spela varje maskin och i vilken ordning de ska spelas, och om du ska fortsätta med den aktuella maskinen eller prova en annan maskin. Problemet med flerarmade banditer faller också in i den breda kategorin stokastisk schemaläggning .

I problemet ger varje maskin en slumpmässig belöning från en sannolikhetsfördelning som är specifik för den maskinen, som inte är känd a-priori. Målet med spelaren är att maximera summan av belöningar som tjänas in genom en sekvens av spakdrag. Den avgörande kompromissen som spelaren står inför vid varje test är mellan "utnyttjande" av den maskin som har den högsta förväntade utdelningen och "utforskning" för att få mer information om de förväntade utdelningarna för de andra maskinerna. Avvägningen mellan utforskning och exploatering står också inför i maskininlärning . I praktiken har flerarmade banditer använts för att modellera problem som att hantera forskningsprojekt i en stor organisation, som en vetenskapsstiftelse eller ett läkemedelsföretag . I tidiga versioner av problemet börjar spelaren utan att ha någon första kunskap om maskinerna.

Herbert Robbins 1952, som insåg vikten av problemet, konstruerade konvergenta befolkningsvalsstrategier i "några aspekter av den sekventiella designen av experiment". Ett teorem, Gittins index , först publicerat av John C. Gittins , ger en optimal policy för att maximera den förväntade rabatterade belöningen.

Empirisk motivation

Hur måste en given budget fördelas mellan dessa forskningsavdelningar för att maximera resultatet?

Det flerarmade banditproblemet modellerar en agent som samtidigt försöker skaffa ny kunskap (kallad "utforskning") och optimera sina beslut baserat på befintlig kunskap (kallad "exploatering"). Agenten försöker balansera dessa konkurrerande uppgifter för att maximera deras totala värde under den tidsperiod som avses. Det finns många praktiska tillämpningar av banditmodellen, till exempel:

• kliniska prövningar som undersöker effekterna av olika experimentella behandlingar samtidigt som patientförlusterna minimeras,
• adaptiva routinginsatser för att minimera förseningar i ett nätverk,
• finansiell portföljdesign

I dessa praktiska exempel kräver problemet att balansera belöningsmaximering baserat på den kunskap som redan förvärvats med försök till nya åtgärder för att ytterligare öka kunskapen. Detta är känt som avvägningen mellan exploatering och utforskning inom maskininlärning .

Modellen har också använts för att styra dynamisk allokering av resurser till olika projekt, för att svara på frågan om vilket projekt man ska arbeta med, givet osäkerhet om svårighetsgraden och utdelningen av varje möjlighet.

Ursprungligen ansett av allierade forskare under andra världskriget , visade det sig så svårlöst att, enligt Peter Whittle , föreslogs att problemet skulle släppas över Tyskland så att tyska forskare också kunde slösa sin tid på det.

Den version av problemet som nu ofta analyseras formulerades av Herbert Robbins 1952.

Den flerarmade banditmodellen

Den flerarmade banditen (kort: bandit eller MAB) kan ses som en uppsättning verkliga fördelningar $B=\{R_{1},\dots ,R_{K }\}$ , varje utdelning är associerad med belöningarna som levereras av en av spakarna $K\in \mathbb {N} ^{+}$ . Låt $\mu _{1},\dots ,\mu _{K}$ vara medelvärdena associerade med dessa belöningsfördelningar. Spelaren spelar iterativt en spak per runda och observerar den tillhörande belöningen. Målet är att maximera summan av de insamlade belöningarna. Horisonten $H$ är antalet omgångar som återstår att spela. Banditproblemet är formellt likvärdigt med en enstats Markov-beslutsprocess . Ångern $\rho$ efter $\displaystyle T}$ { -omgångar definieras som den förväntade skillnaden mellan belöningssumman förknippad med en optimal strategi och summan av de insamlade belöningarna:

$\rho =T\mu ^{*}-\summa _{t=1}^{T}{\widehat {r}}_{t }$ ,

där $\mu ^{*}$ är det maximala belöningsmedelvärdet, $\mu ^{*}=\max _{k}\{\mu _{ k}\}$ , och ${\widehat {r}}_{t}$ är belöningen i omgång t .

En noll-regret-strategi är en strategi vars genomsnittliga ånger per runda $\rho /T$ tenderar till noll med sannolikhet 1 när antalet spelade rundor tenderar till oändligt. Intuitivt kommer strategier med noll ånger garanterat att konvergera till en (inte nödvändigtvis unik) optimal strategi om tillräckligt många omgångar spelas.

Variationer

En vanlig formulering är binär flerarmad bandit eller Bernoulli flerarmad bandit, som ger en belöning på en med sannolikheten $p$ , och annars en belöning på noll.

En annan formulering av den flerarmade banditen har varje arm som representerar en oberoende Markov-maskin. Varje gång en viss arm spelas, avancerar maskinens tillstånd till en ny, vald enligt Markovs tillståndsutvecklingssannolikheter. Det finns en belöning beroende på maskinens aktuella tillstånd. I en generalisering som kallas det "rastlösa banditproblemet" kan tillstånden för icke-spelade vapen också utvecklas över tiden. Det har också diskuterats system där antalet val (om vilken arm man ska spela) ökar över tid.

Datavetenskapsforskare har studerat flerarmade banditer under värsta tänkbara antaganden, och erhållit algoritmer för att minimera ånger i både ändliga och oändliga ( asymptotiska ) tidshorisonter för både stokastiska och icke-stokastiska armutdelningar.

Banditstrategier

Ett stort genombrott var konstruktionen av optimala befolkningsurvalsstrategier, eller policyer (som har en enhetlig maximal konvergensgrad till befolkningen med högsta medelvärde) i arbetet som beskrivs nedan.

Optimala lösningar

Ytterligare information: Gittins index

I artikeln "Asymptotically efficient adaptive allocation rules" konstruerade Lai och Robbins (efter artiklar från Robbins och hans medarbetare som går tillbaka till Robbins år 1952) konvergenta befolkningsurvalspolicyer som har den snabbaste konvergenshastigheten (till befolkningen med högsta medelvärde) för det fall att befolkningens belöningsfördelningar är den exponentiella familjen med en parameter. Sedan, i Katehakis och Robbins , gavs förenklingar av policyn och huvudbeviset för fallet med normala populationer med kända varianser. Nästa anmärkningsvärda framsteg erhölls av Burnetas och Katehakis i uppsatsen "Optimal adaptive policys for sequential allocation problems", där indexbaserade policyer med enhetligt maximal konvergenshastighet konstruerades, under mer allmänna förhållanden som inkluderar fallet där fördelningarna av utfall från varje population beror på en vektor med okända parametrar. Burnetas och Katehakis (1996) gav också en explicit lösning för det viktiga fallet där fördelningarna av utfall följer godtyckliga (dvs icke-parametriska) diskreta, univariata fördelningar.

Senare i "Optimal adaptive policys for Markov decision processes" studerade Burnetas och Katehakis den mycket större modellen av Markov Decision Processes under partiell information, där övergångslagen och/eller den förväntade belöningen för en period kan bero på okända parametrar. I detta arbete konstruerade författarna en explicit form för en klass av adaptiva policyer med enhetligt maximala konvergenshastighetsegenskaper för den totala förväntade belöningen med ändlig horisont under tillräckliga antaganden om ändliga tillståndshandlingsutrymmen och irreducerbarhet av övergångslagen. Ett huvuddrag i dessa policyer är att valet av åtgärder, vid varje tillstånd och tidsperiod, baseras på index som är inflationer på höger sida av de uppskattade genomsnittliga belöningsoptimalitetsekvationerna. Dessa inflationer har nyligen kallats det optimistiska tillvägagångssättet i Tewari och Bartletts, Ortner Filippis, Cappés och Gariviers och Hondas och Takemuras arbete.

För Bernoulli flerarmade banditer, Pilarski et al. studerade beräkningsmetoder för att härleda helt optimala lösningar (inte bara asymptotiskt) med hjälp av dynamisk programmering i tidningen "Optimal Policy for Bernoulli Bandits: Computation and Algorithm Gauge." Via indexeringsscheman, uppslagstabeller och andra tekniker gav detta arbete praktiskt taget tillämpbara optimala lösningar för Bernoulli-banditer förutsatt att tidshorisonter och antal armar inte blev överdrivet stora. Pilarski et al. utökade senare detta arbete i "Delayed Reward Bernoulli Bandits: Optimal Policy and Predictive Meta-Algorithm PARDI" för att skapa en metod för att bestämma den optimala policyn för Bernoulli-banditer när belöningar kanske inte avslöjas omedelbart efter ett beslut och kan försenas. Denna metod bygger på att beräkna förväntade värden för belöningsresultat som ännu inte har avslöjats och uppdatering av posteriora sannolikheter när belöningar avslöjas.

När optimala lösningar på flerarmade bandituppgifter används för att härleda värdet av djurens val, kodar aktiviteten hos neuroner i amygdala och ventral striatum värdena som härrör från dessa policyer, och kan användas för att avkoda när djuren gör utforskande kontra exploaterande val. Dessutom förutsäger optimal policy bättre djurens valbeteende än alternativa strategier (beskrivs nedan). Detta tyder på att de optimala lösningarna på flerarmsbanditproblem är biologiskt rimliga, trots att de är beräkningskrävande.

Ungefärliga lösningar

Det finns många strategier som ger en ungefärlig lösning på banditproblemet, och kan sättas in i de fyra breda kategorierna som beskrivs nedan.

Halvlikformiga strategier

Semi-uniforma strategier var de tidigaste (och enklaste) strategierna som upptäcktes för att ungefär lösa banditproblemet. Alla dessa strategier har gemensamt ett girigt beteende där den bästa spaken (baserat på tidigare observationer) alltid dras utom när en (enhetligt) slumpmässig åtgärd vidtas.

• Epsilon-girig strategi : Den bästa spaken väljs för en proportion $1-\epsilon$ av försöken, och en spak väljs slumpmässigt (med enhetlig sannolikhet) för en proportion $\epsilon$ . Ett typiskt parametervärde kan vara ${\displaystyle \epsilon =0.1} ,$ men detta kan variera kraftigt beroende på omständigheter och förutsägelser.
• Epsilon-första strategi : En ren utforskningsfas följs av en ren exploateringsfas. För $N$ försök upptar utforskningsfasen $\epsilon N$ försök och exploateringsfasen $(1-\epsilon )N$ försök. Under utforskningsfasen väljs en spak slumpmässigt (med enhetlig sannolikhet); under exploateringsfasen väljs alltid den bästa spaken.
• Epsilon-minskande strategi : Liknar den epsilon-giriga strategin, förutom att värdet på $\epsilon$ minskar allt eftersom experimentet fortskrider, vilket resulterar i ett mycket utforskande beteende i början och ett mycket exploaterande beteende i slutet .
• Adaptiv epsilon-girig strategi baserad på värdeskillnader (VDBE) : Liknar den epsilon-minskande strategin, förutom att epsilon reduceras på basis av inlärningsframstegen istället för manuell inställning (Tokic, 2010). Höga fluktuationer i värdeskattningarna leder till en hög epsilon (hög prospektering, låg exploatering); låga fluktuationer till låg epsilon (låg prospektering, hög exploatering). Ytterligare förbättringar kan uppnås genom ett softmax -vägt åtgärdsval vid utforskande åtgärder (Tokic & Palm, 2011).
• Adaptiv epsilon-girig strategi baserad på Bayesianska ensembler (Epsilon-BMC) : En adaptiv epsilon-anpassningsstrategi för förstärkningsinlärning liknande VBDE, med monotona konvergensgarantier. I detta ramverk ses epsilon-parametern som förväntan på en bakre fördelning som väger en girig agent (som litar fullt ut på den lärda belöningen) och en enhetlig inlärningsagent (som misstror den inlärda belöningen). Denna posterior uppskattas med hjälp av en lämplig Beta-fördelning under antagandet om normalitet för observerade belöningar. För att ta itu med den möjliga risken för att minska epsilon för snabbt, modelleras och uppdateras också osäkerheten i variansen av den inlärda belöningen med en normal gamma-modell. (Gimelfarb et al., 2019).

Sannolikhetsmatchningsstrategier

Sannolikhetsmatchningsstrategier återspeglar idén att antalet drag för en given spak bör matcha dess faktiska sannolikhet att vara den optimala spaken. Sannolikhetsmatchningsstrategier är också kända som Thompson-sampling eller Bayesian Bandits, och är förvånansvärt lätta att implementera om du kan prova från baksidan för medelvärdet för varje alternativ.

Sannolikhetsmatchningsstrategier tillåter också lösningar på så kallade kontextuella banditproblem.

Prissättningsstrategier

Prissättningsstrategier fastställer ett pris för varje spak. Till exempel, som illustreras med POKER-algoritmen, kan priset vara summan av den förväntade belöningen plus en uppskattning av extra framtida belöningar som kommer att vinnas genom den ytterligare kunskapen. Spaken för högsta pris dras alltid.

Kontextuell bandit

En användbar generalisering av den flerarmade banditen är den kontextuella flerarmade banditen. Vid varje iteration måste en agent fortfarande välja mellan armar, men de ser också en d-dimensionell funktionsvektor, den kontextvektor som de kan använda tillsammans med belöningarna från de armar som spelades tidigare för att välja vilken arm som ska spelas. Med tiden är elevens mål att samla in tillräckligt med information om hur kontextvektorerna och belöningarna förhåller sig till varandra, så att den kan förutsäga den näst bästa armen att spela genom att titta på funktionsvektorerna.

Ungefärliga lösningar för kontextuell bandit

Det finns många strategier som ger en ungefärlig lösning på det kontextuella banditproblemet och kan delas in i två breda kategorier som beskrivs nedan.

Linjära banditer online

• LinUCB (Upper Confidence Bound) algoritm : författarna antar ett linjärt beroende mellan den förväntade belöningen av en handling och dess sammanhang och modellerar representationsutrymmet med hjälp av en uppsättning linjära prediktorer.
• LinRel (Linear Associative Reinforcement Learning) algoritm : Liknar LinUCB, men använder Singular-value-nedbrytning snarare än Ridge-regression för att få en uppskattning av konfidens.

Online icke-linjära banditer

• UCBogram-algoritm : De olinjära belöningsfunktionerna uppskattas med hjälp av en bitvis konstant estimator som kallas ett regressogram i icke-parametrisk regression . Därefter används UCB på varje konstant del. Successiva förbättringar av uppdelningen av kontextutrymmet schemaläggs eller väljs adaptivt.
• Generaliserade linjära algoritmer : Belöningsfördelningen följer en generaliserad linjär modell, en utökning till linjära banditer.
• KernelUCB-algoritm : en kerneliserad icke-linjär version av linearUCB, med effektiv implementering och ändlig tidsanalys.
• Bandit Forest-algoritm : en slumpmässig skog byggs och analyseras med den slumpmässiga skogen som byggs med kännedom om den gemensamma fördelningen av sammanhang och belöningar.
• Oracle-baserad algoritm : Algoritmen reducerar det kontextuella banditproblemet till en serie av övervakade inlärningsproblem och förlitar sig inte på typiska realiserbarhetsantaganden på belöningsfunktionen.

Begränsad kontextuell bandit

I praktiken är det vanligtvis en kostnad förknippad med resursen som förbrukas av varje åtgärd och den totala kostnaden begränsas av en budget i många applikationer som crowdsourcing och kliniska prövningar. Constrained contextual bandit (CCB) är en sådan modell som tar hänsyn till både tids- och budgetbegränsningar i en flerarmad banditmiljö. A. Badanidiyuru et al. studerade först kontextuella banditer med budgetrestriktioner, även kallade Resourceful Contextual Bandits, och visade att en $O({\sqrt {T}})$ ånger är möjlig. Men deras arbete fokuserar på en begränsad uppsättning policyer, och algoritmen är beräkningsmässigt ineffektiv.

Ram för UCB-ALP för begränsade kontextuella banditer

En enkel algoritm med logaritmisk ånger föreslås i:

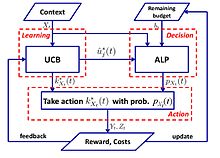
• UCB-ALP-algoritm : Ramverket för UCB-ALP visas i den högra bilden. UCB-ALP är en enkel algoritm som kombinerar UCB-metoden med en adaptiv linjär programmering (ALP) algoritm, och som enkelt kan användas i praktiska system. Det är det första verket som visar hur man uppnår logaritmisk ånger i begränsade kontextuella banditer. Även om det är ägnat åt ett specialfall med en enda budgetbegränsning och fast kostnad, belyser resultaten design och analys av algoritmer för mer allmänna CCB-problem.

Motstridig bandit

En annan variant av det flerarmade banditproblemet kallas den kontradiktoriska banditen, först introducerad av Auer och Cesa-Bianchi (1998). I denna variant, vid varje iteration, väljer en agent en arm och en motståndare väljer samtidigt utdelningsstrukturen för varje arm. Detta är en av de starkaste generaliseringarna av banditproblemet eftersom det tar bort alla antaganden om fördelningen och en lösning på det kontradiktoriska banditproblemet är en generaliserad lösning på de mer specifika banditproblemen.

Exempel: Itererat fångens dilemma

Ett exempel som ofta övervägs för fientliga banditer är det upprepade fångens dilemma . I det här exemplet har varje motståndare två armar att dra. De kan antingen förneka eller bekänna. Standard stokastiska banditalgoritmer fungerar inte särskilt bra med dessa iterationer. Till exempel, om motståndaren samarbetar i de första 100 omgångarna, defekter för de nästa 200, sedan samarbetar i de följande 300, etc. så kommer algoritmer som UCB inte att kunna reagera särskilt snabbt på dessa förändringar. Detta beror på att suboptimala armar efter en viss punkt sällan dras för att begränsa utforskning och fokusera på exploatering. När miljön förändras kan algoritmen inte anpassa sig eller kanske inte ens upptäcka förändringen.

Ungefärliga lösningar

Exp3

EXP3 är en populär algoritm för motstridiga flerarmade banditer, föreslagen och analyserad i denna miljö av Auer et al. [2002b]. Nyligen har det funnits ett ökat intresse för prestandan av denna algoritm i den stokastiska miljön, på grund av dess nya tillämpningar för stokastiska flerarmade banditer med sidoinformation [Seldin et al., 2011] och för flerarmade banditer i blandade stokastiska banditer. kontradiktorisk miljö [Bubeck och Slivkins, 2012]. Uppsatsen presenterade en empirisk utvärdering och förbättrad analys av prestandan för EXP3-algoritmen i den stokastiska miljön, samt en modifiering av EXP3-algoritmen som kan uppnå "logaritmisk" ånger i stokastisk miljö

Algoritm

 
 
  
 
        
 
       Parametrar:  Real $\gamma \in (0,1]$ Initiering: $\omega _{i}(1)=1$ för $i=1,...,K$ För varje  t = 1, 2, ..., T 1. Ställ in ${\displaystyle p_{i}(t)=(1-\gamma ){\frac {\omega _{i}(t)}{\sum _{ j=1}^{K}\omega _{j}(t)}}+{\frac {\gamma }{K}}} i = 1 , . . .$$.. .,K}$ 2. Rita $i_{t}$ slumpmässigt enligt sannolikheterna $p_{1}(t),.. .,p_{K}(t)$ 3. Ta emot belöning $x_{i_{t}}(t)\in [0,1]$ 4. För $j=1,...,K$ set: ${ \displaystyle {\hat {x}}_{j}(t)={\begin{cases}x_{j}(t)/p_{j}(t)&{\text{if }}j=i_{ t}\\0,&{\text{annars}}\end{fall}}}$$\omega _{j}(t+1)=\omega _{j}(t)\exp(\gamma {\hat {x}}_{j}(t)/K)$

Förklaring

Exp3 väljer en arm slumpmässigt med sannolikhet $(1-\gamma )$ den föredrar armar med högre vikt (exploatering), den väljer med sannolikhet $\gamma$ för att likformigt slumpmässigt utforska. Efter att ha mottagit belöningarna uppdateras vikterna. Den exponentiella tillväxten ökar avsevärt vikten av bra armar.

Ångrar analys

Exp3-algoritmens (externa) ånger är högst $O({\sqrt {KTlog(K)}})$

Följ den störda ledaren (FPL) algoritmen

Algoritm

 
 
  
 
  Parametrar:  Real $\eta$ Initialisering: $\forall i:R_{i}(1)=0$ För varje  t = 1,2,..., T 1. För varje arm generera ett slumpmässigt brus från en exponentialfördelning $\forall i:Z_{i}(t)\sim Exp(\eta )$ 2. Dra arm $I(t)$ : $I(t)=arg \max _{i}\{R_{i}(t)+Z_{i}(t)\}$ Lägg till brus till varje arm och dra den med det högsta värdet 3. Uppdatera värde: $R_{I(t)}(t+1)=R_{I(t)}(t)+x_ {I(t)}(t)$ Resten förblir detsamma 

Förklaring

Vi följer den arm som vi tror har den bästa prestandan hittills och lägger till exponentiellt brus för att ge utforskning.

Exp3 vs FPL

Exp3	FPL
Bibehåller vikter för varje arm för att beräkna dragsannolikhet	Behöver inte veta dragsannolikheten per arm
Har effektiva teoretiska garantier	Standard FPL har inga bra teoretiska garantier
Kan vara beräkningsmässigt dyrt (beräkna exponentiella termer)	Beräkningsmässigt ganska effektiv

Oändligt beväpnad bandit

I originalspecifikationen och i ovanstående varianter specificeras banditproblemet med ett diskret och ändligt antal armar, ofta indikerat med variabeln $K$ . I det oändliga armerade fallet, introducerat av Agrawal (1995), är "armarna" en kontinuerlig variabel i $K$ -dimensioner.

Icke-stationär bandit

Detta ramverk hänvisar till det flerarmade banditproblemet i en icke-stationär miljö (dvs i närvaro av konceptdrift ). I den icke-stationära inställningen antas det att den förväntade belöningen för en arm $k$ kan ändras vid varje steg $t\in {\mathcal {T}}$ : $\mu _{t-1}^{k}\neq \mu _{t}^{k}$ . Således $\mu _{t}^{k}$ inte längre hela sekvensen av förväntade (stationära) belöningar för arm $k$ . Istället anger $\mu ^{k}$ sekvensen av förväntade belöningar för arm $k$ , definierad som $\mu ^{ k}=\{\mu _{t}^{k}\}_{t=1}^{T}$ .

Ett dynamiskt orakel representerar den optimala policyn att jämföra med andra policyer i den icke-stationära miljön. Det dynamiska oraklet optimerar den förväntade belöningen vid varje steg $t\in {\mathcal {T}}$ genom att alltid välja den bästa armen, med en förväntad belöning på $\mu _{t} ^{*}$ . Således definieras den kumulativa förväntade belöningen ${\mathcal {D}}(T)$ för det dynamiska oraklet vid sluttidssteg ${\displaystyle T} som:$

${\mathcal {D}}(T)=\summa _{t=1}^{T}{\mu _{t}^{*} }$

Därför beräknas ångern $\rho ^{\pi }(T)$ för policy $\pi$ som skillnaden mellan ${\mathcal {D }}(T)$ och den kumulativa förväntade belöningen i steg $T$ för policy $\pi$ :

$\rho ^{\pi }(T)=\summa _{t=1}^{T}{\mu _{t}^{*}}-\mathbb {E} _{\pi }^{\mu }\ vänster[\sum _{t=1}^{T}{r_{t}}\right]={\mathcal {D}}(T)-\mathbb {E} _{\pi }^{\mu } \left[\sum _{t=1}^{T}{r_{t}}\right]$

Garivier och Moulines härleder några av de första resultaten med avseende på banditproblem där den underliggande modellen kan förändras under spel. Ett antal algoritmer presenterades för att hantera detta fall, inklusive Discounted UCB och Sliding-Window UCB. Ett liknande tillvägagångssätt baserat på Thompson Sampling-algoritm är f-Discounted-Sliding-Window Thompson Sampling (f-dsw TS) som föreslagits av Cavenaghi et al. F-dsw TS-algoritmen utnyttjar en rabattfaktor på belöningshistoriken och ett armrelaterat glidfönster för att kontrastera konceptdrift i icke-stationära miljöer. Ett annat verk av Burtini et al. introducerar en viktad minsta kvadraters Thompson samplingsmetod (WLS-TS), som visar sig vara fördelaktig i både kända och okända icke-stationära fall.

Andra varianter

Många varianter av problemet har föreslagits under senare år.

Duellerande bandit

Duellbanditvarianten introducerades av Yue et al. (2012) för att modellera kompromissen mellan utforskning och exploatering för relativ feedback. I denna variant tillåts spelaren dra två spakar samtidigt, men de får bara en binär feedback som talar om vilken spak som gav den bästa belöningen. Svårigheten med detta problem beror på det faktum att spelaren inte har något sätt att direkt observera belöningen av sina handlingar. De tidigaste algoritmerna för detta problem är InterleaveFiltering, Beat-The-Mean. Den relativa återkopplingen från duellerande banditer kan också leda till röstparadoxer . En lösning är att ta Condorcet-vinnaren som referens.

På senare tid har forskare generaliserat algoritmer från traditionell MAB till duellerande banditer: Relative Upper Confidence Bounds (RUCB), Relative Exponential Weighting (REX3), Copeland Confidence Bounds (CCB), Relative Minimum Empirical Divergence (RMED) och Double Thompson Sampling (DTS) ).

Samarbetande bandit

De kollaborativa filtreringsbanditerna (dvs COFIBA) introducerades av Li och Karatzoglou och Gentile (SIGIR 2016), där den klassiska kollaborativa filtreringen och innehållsbaserade filtreringsmetoderna försöker lära sig en statisk rekommendationsmodell givet träningsdata. Dessa tillvägagångssätt är långt ifrån idealiska i mycket dynamiska rekommendationsdomäner som nyhetsrekommendationer och beräkningsreklam, där uppsättningen av objekt och användare är mycket flytande. I det här arbetet undersöker de en adaptiv klustringsteknik för innehållsrekommendationer baserad på utforskning-exploateringsstrategier i kontextuella flerarmade banditmiljöer. Deras algoritm (COFIBA, uttalas som "Coffee Bar") tar hänsyn till de samarbetseffekter som uppstår på grund av användarnas interaktion med föremålen, genom att dynamiskt gruppera användare baserat på föremålen som övervägs och samtidigt gruppera föremålen baserat på likheten mellan klustringarna som induceras över användarna. Den resulterande algoritmen drar alltså fördel av preferensmönster i data på ett sätt som liknar kollaborativa filtreringsmetoder. De tillhandahåller en empirisk analys av medelstora datauppsättningar i den verkliga världen, som visar skalbarhet och ökad prediktionsprestanda (mätt med klickfrekvens) jämfört med toppmoderna metoder för klustring av banditer. De ger också en ångeranalys inom en standardinställning för linjär stokastisk brus.

Kombinatorisk bandit

Problemet med Combinatorial Multiarmed Bandit (CMAB) uppstår när istället för en enda diskret variabel att välja mellan, måste en agent välja värden för en uppsättning variabler. Om man antar att varje variabel är diskret, är antalet möjliga val per iteration exponentiellt i antalet variabler. Flera CMAB-inställningar har studerats i litteraturen, från inställningar där variablerna är binära till mer generella inställningar där varje variabel kan ta en godtycklig uppsättning värden.

Se även

• Gittins index – en kraftfull, allmän strategi för att analysera banditproblem.
• Girig algoritm
• Optimalt stopp
• Sökteori
• Stokastisk schemaläggning

Vidare läsning

• Guha, S.; Munagala, K.; , "Approximation algorithms for restless bandit problems", Journal of the ACM , 58 : 1–50, arXiv : 0711.3861 , doi : 10.1145/1870103.1870106 , S54CID 6 , S54CID  
• Dayanik, S.; Powell, W.; Yamazaki, K. (2008), "Indexpolicyer för rabatterade banditproblem med tillgänglighetsbegränsningar", Advances in Applied Probability , 40 (2): 377–400, doi : 10.1239/aap/1214950209 .
•   Powell, Warren B. (2007), "Kapitel 10", Approximate Dynamic Programming: Solving the Curses of Dimensionality , New York: John Wiley and Sons, ISBN 978-0-470-17155-4 .
• Robbins, H. (1952), "Some aspects of the sequential design of experiments", Bulletin of the American Mathematical Society , 58 (5): 527–535, doi : 10.1090/S0002-9904-1952-09620-8 .
•   Sutton, Richard; Barto, Andrew (1998), Reinforcement Learning , MIT Press, ISBN 978-0-262-19398-6 , arkiverad från originalet 2013-12-11 .

•    Allesiardo, Robin (2014), "A Neural Networks Committee for the Contextual Bandit Problem", Neural Information Processing – 21st International Conference, ICONIP 2014, Malaisia, 03-06 november 2014, Proceedings , Lecture Notes in Computer Science, vol. 8834, Springer, s. 374–381, arXiv : 1409.8191 , doi : 10.1007/978-3-319-12637-1_47 , ISBN 978-3-319-12626-5CID 71 , 84 S

•   Weber, Richard (1992), "On the Gittins index for multiarmed bandits", Annals of Applied Probability , 2 (4): 1024–1033, doi : 10.1214/aoap/1177005588 , JSTOR 2959678 .
•    Katehakis, M .; C. Derman (1986), "Computing optimal sequential allocation rules in clinical trials", Adaptiva statistiska procedurer och relaterade ämnen, Institute of Mathematical Statistics Lecture Notes - Monograph Series, vol. 8, s. 29–39, doi : 10.1214/lnms/1215540286 , ISBN 978-0-940600-09-6 , JSTOR 4355518 .
•    Katehakis, M .; AF Veinott, Jr. (1987), "The multi-armed bandit problem: decomposition and computation" , Mathematics of Operations Research , 12 (2): 262–268, doi : 10.1287/moor.12.2.262 , JSTOR 3689689 , S 656323 .

externa länkar

• MABWiser , öppen källkod Python-implementering av banditstrategier som stöder kontextfria, parametriska och icke-parametriska kontextuella policyer med inbyggd parallellisering och simuleringsmöjlighet.
• PyMaBandits , öppen källkod implementering av banditstrategier i Python och Matlab.
• Kontextuellt R- paket med öppen källkod som underlättar simulering och utvärdering av både kontextfria och kontextuella Multi-Armed Bandit-policyer .
• bandit.sourceforge.net Bandit-projekt , öppen källkod implementering av banditstrategier.
• Banditlib , Open-Source implementering av banditstrategier i C++.
• Leslie Pack Kaelbling och Michael L. Littman (1996). Exploatering kontra utforskning: The Single-State Case .
• Handledning: Introduktion till banditer: Algoritmer och teori. Del 1 . Del 2 .
• Feynmans restaurangproblem , ett klassiskt exempel (med känt svar) på avvägningen mellan exploatering och utforskning.
• Banditalgoritmer kontra AB-testning .
• S. Bubeck och N. Cesa-Bianchi En undersökning om banditer .
• En undersökning om kontextuella flerarmade banditer , en undersökning/handledning för kontextuella banditer.
• Blogginlägg om flerarmade banditstrategier, med Python-kod .
• Animerade, interaktiva plot som illustrerar Epsilon-giriga, Thompson-sampling och upper Confidence Bound-utforsknings-/exploateringsstrategier.