Fermat punkt

Fig 1. Konstruktion av det första isogoniska centret, X(13). När ingen vinkel på triangeln överstiger 120° är denna punkt Fermatpunkten.

I euklidisk geometri är Fermatpunkten i en triangel , även kallad Torricellipunkten eller Fermat–Torricellipunkten , en punkt sådan att summan av de tre avstånden från var och en av triangelns tre hörn till punkten är den minsta möjliga eller , motsvarande den geometriska medianen för de tre hörnen. Det heter så eftersom detta problem först togs upp av Fermat i ett privat brev till Evangelista Torricelli , som löste det.

Fermat-punkten ger en lösning på geometriska median- och Steinerträdproblem för tre punkter.

Konstruktion

Fermatpunkten i en triangel med största vinkel som högst 120° är helt enkelt dess första isogoniska centrum eller X(13) , som är konstruerad enligt följande:

1. Konstruera en liksidig triangel på var och en av två godtyckligt valda sidor av den givna triangeln.
2. Rita en linje från varje ny hörn till den motsatta hörn av den ursprungliga triangeln.
3. De två linjerna skär varandra vid Fermat-punkten.

En alternativ metod är följande:

1. På var och en av två godtyckligt valda sidor, konstruera en likbent triangel , med basen på sidan i fråga, 30-graders vinklar vid basen och den tredje spetsen av varje likbent triangel som ligger utanför den ursprungliga triangeln.
2. Rita en cirkel för varje likbent triangel, i varje fall med mitten på den likbenta triangelns nya vertex och med radien lika med var och en av de två nya sidorna i den likbenta triangeln.
3. Skärningspunkten inuti den ursprungliga triangeln mellan de två cirklarna är Fermat-punkten.

När en triangel har en vinkel som är större än 120°, är Fermat-punkten placerad vid den trubbvinklade vertexen.

I det följande betyder "Fall 1" att triangeln har en vinkel som överstiger 120°. "Fall 2" betyder att ingen vinkel på triangeln överstiger 120°.

Plats för X(13)

Fig 2. Geometri för det första isogoniska centret.

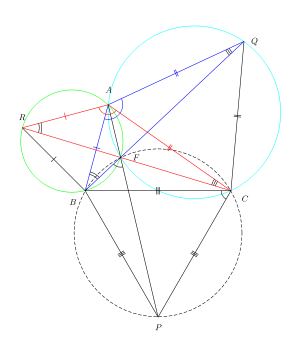
Fig. 2 visar de liksidiga trianglarna △ ARB , △ AQC , △ CPB fästa vid sidorna av den godtyckliga triangeln △ ABC . Här är ett bevis som använder egenskaper för koncykliska punkter för att visa att de tre linjerna RC, BQ, AP i Fig. 2 alla skär varandra i punkten F och skär varandra i vinklar på 60°.

Trianglarna △ RAC , △ BAQ är kongruenta eftersom den andra är en 60° rotation av den första om A . Därför ∠ ARF = ∠ ABF och ∠ AQF = ∠ ACF . Genom motsatsen till den inskrivna vinkelsatsen tillämpad på segmentet AF , är punkterna ARBF koncykliska (de ligger på en cirkel). På samma sätt är punkterna AFCQ koncykliska.

∠ ARB = 60° , alltså ∠ AFB = 120° , med hjälp av den inskrivna vinkelsatsen . På liknande sätt, ∠ AFC = 120° .

Så ∠ BFC = 120° . Därför är ∠ BFC + ∠ BPC = 180° . Med hjälp av den inskrivna vinkelsatsen innebär detta att punkterna BPCF är koncykliska. Så, med hjälp av den inskrivna vinkelsatsen applicerad på segmentet BP , ∠ BFP = ∠ BCP = 60° . Eftersom ∠ BFP + ∠ BFA = 180° , ligger punkten F på linjesegmentet AP . Så, linjerna RC, BQ, AP är samtidiga (de skär varandra i en enda punkt). QED

Detta bevis gäller endast i fall 2, eftersom om ∠ BAC > 120° ligger punkt A innanför omkretsen av △ BPC som växlar de relativa positionerna för A och F . Det är dock lätt att modifiera för att täcka fall 1. Då ∠ AFB = ∠ AFC = 60° därav ∠ BFC = ∠ AFB + ∠ AFC = 120° vilket betyder att BPCF är koncyklisk så ∠ BFP = ∠ BCP = 60° = ∠ BFA . Därför ligger A på FP .

Linjerna som förenar cirklarnas mittpunkter i fig. 2 är vinkelräta mot linjesegmenten AP , BQ , CR . Till exempel är linjen som förenar mitten av cirkeln som innehåller △ ARB och mitten av cirkeln som innehåller △ AQC , vinkelrät mot segmentet AP . Så linjerna som förenar cirklarnas centrum skär också i 60° vinklar. Därför bildar cirklarnas mittpunkter en liksidig triangel. Detta är känt som Napoleons sats .

Platsen för Fermat-punkten

Traditionell geometri

Fig 3. Fermatpunktens geometri

Givet en euklidisk triangel △ ABC och en godtycklig punkt P låt $d(P)=|PA|+|PB|+|PC|.$ Syftet med detta avsnitt är att identifiera en punkt P ₀ så att $d(P_{ 0})<d(P)$ för alla $P\neq P_{0}.$ Om en sådan punkt finns kommer det att vara Fermat-punkten. I det följande Δ att beteckna punkterna inuti triangeln och kommer att anses innefatta dess gräns Ω .

Ett nyckelresultat som kommer att användas är dogleg-regeln, som hävdar att om en triangel och en polygon har en sida gemensam och resten av triangeln ligger inuti polygonen så har triangeln en kortare omkrets än polygonen:

Om AB är den gemensamma sidan, förläng AC för att skära polygonen vid punkten X . Då är polygonens omkrets, med triangelolikheten :

${\text{perimeter}}>|AB|+|AX|+|XB|=|AB|+|AC|+|CX|+|XB|\geq |AB|+|AC|+|BC |.$

Låt P vara vilken punkt som helst utanför Δ . Associera varje vertex med dess avlägsna zon; det vill säga halvplanet bortom den (förlängda) motsatta sidan. Dessa 3 zoner täcker hela planet utom Δ själv och P ligger tydligt i antingen en eller två av dem. Om P är i två (säg B- och C -zonernas skärningspunkt) så innebär inställningen $P'=A$$d( P')=d(A)<d(P)$ enligt dogleg-regeln. Alternativt om P är i endast en zon, säg A -zonen, då $d(P')<d(P)$ där P' är skärningspunkten mellan AP och BC . Så för varje punkt P utanför Δ finns det en punkt P' i Ω så att $d(P')<d(P).$

Fall 1. Triangeln har en vinkel ≥ 120°.

Antag att vinkeln vid A är ≥ 120° utan förlust av allmänhet. Konstruera den liksidiga triangeln △ AFB och för valfri punkt P i Δ (förutom A själv) konstruera Q så att triangeln △ AQP är liksidig och har den visade orienteringen. Då är triangeln △ ABP en 60° rotation av triangeln △ AFQ kring A så dessa två trianglar är kongruenta och det följer att $d(P)=|CP|+|PQ|+|QF|$ som helt enkelt är längden på sökvägen CPQF . Eftersom P är tvungen att ligga inom △ ABC , överstiger längden på denna väg enligt dogleg-regeln $|AC|+|AF|=d(A).$ Därför, $d(A)<d(P)$ för alla $P\in \Delta ,P\neq A.$ Låt nu P vara utanför Δ . Från ovan finns en punkt $P'\in \Omega$ så att $d(P')<d(P)$ och som $d(A)\leq d(P')$ det följer att $d(A)<d(P)$ för alla P utanför Δ . Således $d(A)<d(P)$ för alla $P\neq A$ vilket betyder att A är Fermatpunkten för Δ . Med andra ord ligger Fermat-punkten vid den trubbvinklade vertexen .

Fall 2. Triangeln har ingen vinkel ≥ 120°.

Konstruera den liksidiga triangeln △ BCD , låt P vara vilken punkt som helst innanför Δ , och konstruera den liksidiga triangeln △ CPQ . Då △ CQD en 60° rotation av △ CPB omkring C so

$d(P)=|PA|+|PB|+|PC|=|AP|+|PQ|+|QD|$

vilket helt enkelt är längden på banan APQD . Låt P ₀ vara punkten där AD och CF skär varandra. Denna punkt kallas vanligtvis det första isogoniska centret. Utför samma övning med P ₀ som du gjorde med P och hitta punkten Q ₀ . Genom vinkelbegränsningen P ₀ inuti △ ABC . Dessutom △ BCF en 60° rotation av △ BDA om B , så Q ₀ måste ligga någonstans på AD . Eftersom ∠ CDB = 60° följer att Q ₀ ligger mellan P ₀ och D vilket betyder att ₀₀ AP Q D är en rät linje så $d(P_{0}=|AD|.$ Dessutom , om $P\neq P_{0}$ så kommer antingen P eller Q inte att ligga på AD vilket betyder $d(P_ {0})=|AD|<d(P).$ Låt nu P vara utanför Δ . Från ovan finns en punkt $P'\in \Omega$ så att $d(P')<d(P)$ och som $d(P_{0})\leq d(P')$ följer det att $d(P_{0})<d(P)$ för alla P utanför Δ . Det betyder att P ₀ är Fermatpunkten för Δ . Med andra ord är Fermatpunkten sammanfallande med det första isogoniska centret .

Vektoranalys

Låt O, A, B, C, X vara vilka fem punkter som helst i ett plan. Beteckna vektorerna ${\overrightarrow {OA}},\ {\overrightarrow {OB}},\ {\overrightarrow {OC}},\ {\ högerpil {OX}}$ med a , b , c , x respektive och låt i , j , k vara enhetsvektorerna från O längs a , b , c .

${\begin{aligned}|\mathbf {a} |&=\mathbf {a\cdot i} =(\mathbf {a} -\mathbf {x} )\mathbf {\,\cdot \,i } +\mathbf {x\cdot i} \leq |\mathbf {a} -\mathbf {x} |+\mathbf {x\cdot i} ,\\|\mathbf {b} |&=\mathbf {b \cdot j} =(\mathbf {b} -\mathbf {x} )\mathbf {\,\cdot \,j} +\mathbf {x\cdot j} \leq |\mathbf {b} -\mathbf { x} |+\mathbf {x\cdot j} ,\\|\mathbf {c} |&=\mathbf {c\cdot k} =(\mathbf {c} -\mathbf {x} )\mathbf {\ ,\cdot \,k} +\mathbf {x\cdot k} \leq |\mathbf {c} -\mathbf {x} |+\mathbf {x\cdot k} .\end{aligned}}$

Att lägga till a , b , c ger

$|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |\leq |\mathbf {a} -\mathbf {x} |+|\mathbf {b} -\ mathbf {x} |+|\mathbf {c} -\mathbf {x} |+x\cdot (\mathbf {i} +\mathbf {j} +\mathbf {k} ).$

Om a , b , c möts vid O i vinklar på 120° så är i + j + k = 0 , så

$|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |\leq |\mathbf {a} -\mathbf {x} |+|\mathbf {b} -\ mathbf {x} |+|\mathbf {c} -\mathbf {x} |$

för alla x . Med andra ord,

$|OA|+|OB|+|OC|\leq |XA|+|XB|+|XC|$

och följaktligen är O Fermatpunkten för △ ABC .

Detta argument misslyckas när triangeln har en vinkel ∠ C > 120° eftersom det inte finns någon punkt O där a , b , c möts i vinklar på 120°. Ändå fixas det enkelt genom att omdefiniera k = − ( i + j ) och placera O vid C så att c = 0 . Observera att | k | ≤ 1 eftersom vinkeln mellan enhetsvektorerna i , j är ∠ C som överstiger 120°. Eftersom

$|\mathbf {0} |\leq |\mathbf {0} -\mathbf {x} |+\mathbf {x\cdot k} ,$

den tredje ojämlikheten kvarstår, de andra två ojämlikheterna är oförändrade. Beviset fortsätter nu som ovan (att lägga till de tre olikheterna och använda i + j + k = 0 ) för att nå samma slutsats att O (eller i det här fallet C ) måste vara Fermatpunkten för △ ABC .

Lagrange multiplikatorer

Ett annat tillvägagångssätt för att hitta punkten inom en triangel, från vilken summan av avstånden till triangelns hörn är minimal, är att använda en av de matematiska optimeringsmetoderna ; specifikt metoden med Lagrange-multiplikatorer och cosinuslagen .

Vi ritar linjer från punkten inom triangeln till dess hörn och kallar dem X , Y , Z . Låt också längden på dessa linjer vara x, y, z respektive. Låt vinkeln mellan X och Y vara α , Y och Z vara β . Då är vinkeln mellan X och Z 2π − α − β . Med hjälp av metoden med Lagrange-multiplikatorer måste vi hitta minimum av Lagrangian L , vilket uttrycks som:

$L=x+y+z+\lambda _{1}(x^{2}+y^ {2}-2xy\cos(\alpha )-a^{2})+\lambda _{2}(y^{2}+z^{2}-2yz\cos(\beta )-b^{2 })+\lambda _{3}(z^{2}+x^{2}-2zx\cos(\alpha +\beta )-c^{2})$

där a, b, c är längderna på triangelns sidor.

Lika var och en av de fem partiella derivatorna ${\tfrac {\partial L}{\partial x}}, \tfrac {\partial L}{\partial y}},{\tfrac {\partial L}{\partial z}},{\tfrac {\partial L}{\partial \alpha }},{\tfrac {\ partiell L}{\partial \beta }}$ till noll och eliminering av λ ₁ , λ ₂ , λ ₃ ger så småningom sin α = sin β och sin( α + β ) = − sin β så α = β = 120° . Men elimineringen är en lång och tråkig affär, och slutresultatet täcker endast fall 2.

Egenskaper

De två isogoniska centran är skärningspunkterna mellan tre vesicae piscis vars parade hörn är triangelns hörn

• När triangelns största vinkel inte är större än 120° är X (13) Fermatpunkten.
• Vinklarna som täcks av triangelns sidor vid X (13) är alla lika med 120° (fall 2), eller 60°, 60°, 120° (fall 1).
• De omslutna cirklarna för de tre konstruerade liksidiga trianglarna är samtidiga vid X (13).
• Trilinjära koordinater för det första isogoniska centret, X (13):

${\begin{aligned}&\csc \left(A+{\tfrac {\pi }{3}}\right):\csc \left(B+{\tfrac {\pi }{3}}\right ):\csc \left(C+{\tfrac {\pi }{3}}\right)\\&=\sec \left(A-{\tfrac {\pi }{6}}\right):\sek \left(B-{\tfrac {\pi }{6}}\right):\sec \left(C-{\tfrac {\pi }{6}}\right).\end{aligned}}$

• Trilinjär koordinater för det andra isogoniska centret, ( 14):

${\begin{aligned}&\csc \left(A-{\tfrac {\pi }{3}}\right):\csc \left(B-{\tfrac {\pi }{3}} \right):\csc \left(C-{\tfrac {\pi }{3}}\right)\\&=\sec \left(A+{\tfrac {\pi }{6}}\right): \sec \left(B+{\tfrac {\pi }{6}}\right):\sec \left(C+{\tfrac {\pi }{6}}\right).\end{aligned}}$

• Trilinjär koordinater för Fermatpunkten:

${\displaystyle 1-u+uvw\sec \left(A-{\tfrac {\pi }{6}}\right):1-v+uvw\sec \left(B-{\tfrac {\ pi }{6}}\right):1-w+uvw\sec \left(C-{\tfrac {\pi }{6}}\right)} där u, v, w respektive$

betecknar de booleska variablerna ( A < 120°), ( B < 120°), ( C < 120°) .

• Det isogonala konjugatet av X (13) är den första isodynamiska punkten , X (15):

$\sin \left(A+{\tfrac {\pi }{3}}\right):\sin \left(B+{\tfrac {\pi }{3}}\right):\sin \left( C+{\tfrac {\pi }{3}}\right).$

• Det isogonala konjugatet av X (14) är den andra isodynamiska punkten , X (16):

$\sin \left(A-{\tfrac {\pi }{3}}\right):\sin \left(B-{\tfrac {\pi }{3}}\right):\sin \ vänster(C-{\tfrac {\pi }{3}}\höger).$

• Följande trianglar är liksidiga:
  • antipedal triangel av X (13)
  • Antipedal triangel av X (14)
  • Pedaltriangel av X (15)
  • Pedaltriangel av X (16)
  • Circumcevian triangel av X (15)
  • Circumcevian triangel av X (16)
• Linjerna X (13) X (15) och X (14) X (16) är parallella med Euler-linjen . De tre linjerna möts vid Eulers oändlighetspunkt, X (30).
• Punkterna X (13), X (14), circumcenter och niopunktscentrum ligger på en Lester-cirkel .
• Linjen X (13) X (14) möter Eulerlinjen vid mittpunkten av X (2) och X (4).
• Fermat-punkten ligger i den öppna ortocentroidala skivan som är punkterad i dess eget centrum och kan vara vilken punkt som helst däri.

Alias

De isogoniska centran X (13) och X (14) är också kända som den första Fermatpunkten respektive den andra Fermatpunkten . Alternativen är den positiva Fermat-punkten och den negativa Fermat-punkten . Men dessa olika namn kan vara förvirrande och är kanske bäst att undvika. Problemet är att mycket av litteraturen suddar ut skillnaden mellan Fermat-punkten och den första Fermat-punkten medan det bara är i fall 2 ovan som de faktiskt är desamma.

Historia

Denna fråga föreslogs av Fermat, som en utmaning till Evangelista Torricelli . Han löste problemet på ett liknande sätt som Fermats, fastän han använde skärningspunkten mellan de omslutna cirklarna av de tre regelbundna trianglarna istället. Hans elev, Viviani, publicerade lösningen 1659.

Se även

• Geometrisk median eller Fermat–Weber-punkt, punkten som minimerar summan av avstånden till mer än tre givna punkter.
• Lesters sats
• Triangel mitt
• Napoleon pekar
• Webers problem

externa länkar

• "Fermat-Torricelli problem" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Fermat Point av Chris Boucher, The Wolfram Demonstrations Project .
• Fermat-Torricelli generalisering vid dynamiska geometriskisser Interaktiv skiss generaliserar Fermat-Torricelli-punkten.
• Ett praktiskt exempel på Fermat-punkten
• iOS interaktiv skiss