Enhetsavståndsgraf

En enhetsavståndsgraf med 16 hörn och 40 kanter

I matematik , särskilt geometrisk grafteori , är en enhetsavståndsgraf en graf som bildas från en samling punkter i det euklidiska planet genom att ansluta två punkter när avståndet mellan dem är exakt en. För att särskilja dessa grafer från en bredare definition som tillåter att vissa icke-angränsande par av hörn ligger på avstånd ett, kan de också kallas strikta enhetsavståndsgrafer eller trogna enhetsavståndsgrafer . Som en ärftlig familj av grafer kan de karakteriseras av förbjudna inducerade subgrafer . Enhetsavståndsgraferna inkluderar kaktusgraferna , tändsticksgraferna och pennygraferna och hyperkubgraferna . De generaliserade Petersen-graferna är icke-strikta enhetsdistansgrafer.

Ett olöst problem av Paul Erdős frågar hur många kanter en enhetsavståndsgraf på $n$ hörn kan ha. Den mest kända $n^{4/3}$ gränsen är något över linjär i $\displaystyle n}$ — långt från den övre gränsen , proportionell mot . Antalet färger som krävs för att färga enhetsdistansgrafer är också okänt ( Hadwiger–Nelson-problemet ): vissa enhetsdistansgrafer kräver fem färger, och varje enhetsdistansgraf kan färgas med sju färger. För varje algebraiskt tal finns det en enhetsavståndsgraf med två hörn som måste vara det avståndet från varandra. Enligt Beckman-Quarles-satsen är de enda planomvandlingarna som bevarar alla enhetsavståndsgrafer isometrierna .

Det är möjligt att konstruera en enhetsdistansgraf effektivt, givet dess punkter. Att hitta alla enhetsavstånd har tillämpningar inom mönstermatchning , där det kan vara ett första steg för att hitta kongruenta kopior av större mönster. Men att avgöra om en given graf kan representeras som en enhetsdistansgraf är NP-svårt , och mer specifikt komplett för den existentiella teorin om verkligheten .

Definition

Petersen -grafen som en enhetsdistansgraf

Möbius –Kantor-grafen som en subgraf till en enhetsdistansgraf

Enhetsavståndsgrafen för en uppsättning punkter i planet är den oriktade grafen med dessa punkter som sina hörn , med en kant mellan två hörn närhelst deras euklidiska avstånd är exakt ett. En abstrakt graf sägs vara en enhetsavståndsgraf om det är möjligt att hitta distinkta platser i planet för dess hörn, så att dess kanter har enhetslängd och så att alla icke intilliggande hörnpar har icke-enhetsavstånd. När detta är möjligt är den abstrakta grafen isomorf till enhetsavståndsgrafen för de valda platserna. Alternativt använder vissa källor en bredare definition, vilket tillåter icke-intilliggande par av hörn att vara på enhetsavstånd. De resulterande graferna är subgraferna för enhetsavståndsgraferna (som definieras här). Där terminologin kan vara tvetydig, kan graferna där icke-kanter måste vara ett avstånd från varandra kallas strikta enhetsavståndsgrafer eller trogna enhetsavståndsgrafer . Undergraferna för enhetsavståndsgrafer är på motsvarande sätt de grafer som kan ritas i planet med endast en kantlängd. För korthetens skull hänvisar den här artikeln till dessa som "icke strikta enhetsdistansdiagram".

Grafer för enhetsavstånd ska inte förväxlas med grafer för enhetsdiskar , som kopplar ihop par av punkter när deras avstånd är mindre än eller lika med ett, och som ofta används för att modellera trådlösa kommunikationsnätverk.

Exempel

Den fullständiga grafen på två hörn är en enhetsdistansgraf, liksom den fullständiga grafen på tre hörn (triangelgrafen ), men inte den fullständiga grafen på fyra hörn. Genom att generalisera triangelgrafen är varje cykelgraf en enhetsdistansgraf, realiserad av en vanlig polygon . Två grafer för ändliga enhetsavstånd, kopplade vid en enda delad vertex, ger ytterligare en enhetsdistansgraf, eftersom den ena kan roteras i förhållande till den andra för att undvika oönskade ytterligare enhetsavstånd. Genom att på så sätt sammankoppla grafer kan varje finit träd eller kaktusgraf realiseras som en enhetsdistansgraf.

Hyperkubgrafen $\displaystyle Q_{4}}$ { har 16 hörn och 32 enhetsavstånd

Hamming -grafen $H(3,3)$ har 27 hörn och 81 enhetsavstånd

Varje kartesisk produkt av enhetsavståndsgrafer ger en annan enhetsdistansgraf; detsamma gäller dock inte för vissa andra vanliga grafprodukter. Till exempel ger den starka produkten av grafer , applicerad på två icke-tomma grafer, kompletta subgrafer med fyra hörn, som inte är grafer för enhetsavstånd. De kartesiska produkterna av väggrafer bildar rutnätsgrafer av vilken dimension som helst, de kartesiska produkterna för hela grafen på två hörn är hyperkubgraferna och de kartesiska produkterna av triangelgrafer är Hamming-graferna $H( d,3)$ .

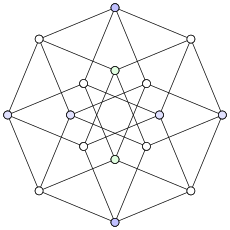
Andra specifika grafer som är enhetsdistansgrafer inkluderar Petersen-grafen , Heawood-grafen , hjulgrafen $W_{7}$ (den enda hjulgrafen som är en enhetsdistansgraf) och Moser-spindel- och Golomb-grafen (små 4- kromatiska enhetsdistansgrafer). Alla generaliserade Petersen-grafer , som Möbius–Kantor-grafen som visas, är icke-strikta enhetsdistansgrafer.

Tändsticksgrafer är ett specialfall av enhetsdistansgrafer, där inga kanter korsar varandra. Varje tändsticksgraf är en plan graf , men vissa i övrigt plana enhetsavståndsgrafer (som Moser-spindeln) har en korsning i varje representation som en enhetsdistansgraf. Dessutom, i samband med grafer för enhetsavstånd, bör termen "plan" användas med försiktighet, eftersom vissa författare använder den för att hänvisa till det plan i vilket enhetsavstånden definieras, snarare än till ett förbud mot korsningar. Penny -graferna är ett ännu mer speciellt fall av enhetsavstånds- och tändsticksgrafer, där varje icke-intilliggande hörnpar är mer än en enhet från varandra.

Egenskaper

Antal kanter

Se även: Erdős distinkta avståndsproblem

Olöst problem i matematik :

Hur många enhetsavstånd kan bestämmas av en uppsättning av $n$ punkter?

(fler olösta problem i matematik)

Paul Erdős ( 1946 ) ställde problemet med att uppskatta hur många par av punkter i en uppsättning av $n$ punkter som kan vara på enhetsavstånd från varandra. I grafteoretiska termer frågar frågan hur tät en enhetsdistansgraf kan vara, och Erdős publikation om denna fråga var ett av de första verken inom extremal grafteorin . Hyperkubgraferna och Hamming-graferna ger en nedre gräns för antalet enhetsavstånd, proportionell mot $n\log n.$ Genom att överväga punkter i ett kvadratiskt rutnät med noggrant utvalt avstånd, fann Erdős en förbättrad nedre gräns för formen

$$n^{1+c/\log \log n}$$

för en konstant $c$ och erbjöd 500 $ för ett bevis på om antalet enhetsavstånd också kan begränsas ovan av en funktion av denna form. Den mest kända övre gränsen för detta problem är

$${\sqrt[{3}]{\frac {29n^{4}}{4}}}\approx 1.936n^{4/3}.$$

Denna gräns kan ses som räkning av incidenser mellan punkter och enhetscirklar, och är nära relaterad till korsningstalets olikhet och till Szemerédi-Trotters sats om incidenser mellan punkter och linjer.

För små värden på $n$ (upp till 14, från och med 2022) är det exakta maximala antalet möjliga kanter känt. För $n=2,3,4,\dots$ är dessa kanter:

1, 3, 5, 7, 9, 12, 14, 18, 20, 23, 27, 30, 33, ... (sekvens A186705 i OEIS )

Förbjudna subgrafer

Om en given graf $G$ inte är en icke-strikt enhetsdistansgraf, är det inte heller någon supergraf $H$ av $G$ . En liknande idé fungerar för strikta enhetsavståndsgrafer, men genom att använda konceptet med en inducerad subgraf , en subgraf bildad från alla kanter mellan paren av hörn i en given undergrupp av hörn. Om $G$ inte är en strikt enhetsdistansgraf, så är det inte heller någon annan $H$ som har $G$ som en inducerad subgraf. På grund av dessa relationer mellan huruvida en subgraf eller dess supergraf är en enhetsavståndsgraf, är det möjligt att beskriva enhetsdistansgrafer med deras förbjudna subgrafer . Dessa är de minimala graferna som inte är enhetsavståndsgrafer av den givna typen. De kan användas för att avgöra om en given graf $G$ är en enhetsdistansgraf, av endera typen. $G$ är en icke-strikt enhetsdistansgraf, om och endast om $G$ inte är en supergraf av en förbjuden graf för de icke-strikta enhetsdistansgraferna. $G$ är en strikt enhetsdistansgraf, om och endast om $G$ inte är en inducerad supergraf av en förbjuden graf för de strikta enhetsdistansgraferna.

För både de icke-strikta och strikta enhetsdistansgraferna inkluderar de förbjudna graferna både den fullständiga grafen $K_{4}$ och den fullständiga tvådelade grafen $K_{2,3}$ . För ${\displaystyle K_{2,3}} ,$ varhelst hörnen på den här grafens tvåpunktssida är placerade, finns det högst två positioner på enhetsavstånd från dem för att placera de andra tre hörnen, så det är omöjligt att placera alla tre hörn på distinkta punkter. Dessa är de enda två förbjudna graferna för de icke-strikta enhetsdistansgraferna på upp till fem hörn; det finns sex förbjudna grafer på upp till sju hörn och 74 på grafer upp till nio hörn. Eftersom limning av två enhetsavståndsgrafer (eller subgrafer därav) vid en vertex ger strikta (respektive icke-strikta) enhetsdistansgrafer, är varje förbjuden graf en tvåkopplad graf , en graf som inte kan bildas av denna limningsprocess.

Hjulgrafen $W_{7}$ kan realiseras som en strikt enhetsdistansgraf med sex av dess hörn som bildar en enhetlig hexagon och den sjunde i mitten av hexagonen. Att ta bort en av kanterna från mittpunkten ger en subgraf som fortfarande har enhetslängdskanter, men som inte är en strikt enhetsdistansgraf. Den regelbundna hexagonplaceringen av dess hörn är det enda sättet ( upp till kongruens ) att placera hörnen på distinkta platser så att intilliggande hörn är ett enhetsavstånd från varandra, och denna placering placerar också de två ändpunkterna av den saknade kanten på enhetsavstånd . Det är alltså en förbjuden graf för graferna för strikt enhetsavstånd, men inte en av de sex förbjudna graferna för de icke-strikta enhetsdistansgraferna. Andra exempel på grafer som är icke-strikta enhetsavståndsgrafer men inte strikta enhetsdistansgrafer inkluderar grafen som bildas genom att ta bort en yttre kant från ${\displaystyle W_{7}} ,$ och sex-vertex-grafen bildad av ett triangulärt prisma genom att ta bort en kant från en av dess trianglar.

Algebraiska tal och stelhet

Huvudartikel: Beckman–Quarles teorem

För varje algebraiskt tal ${\displaystyle \alpha } ,$ är det möjligt att konstruera en enhetsdistansgraf $G$ där ett par hörn är på avståndet $\alpha$ i alla enhetsavståndsrepresentationer av $G$ . Detta resultat antyder en ändlig version av Beckman-Quarles-satsen : för två punkter $p$ och $q$ på avstånd $\alpha$ från varandra, finns det ett ändligt stel enhetsavstånd graf som innehåller $p$ och $q$ så att varje transformation av planet som bevarar enhetsavstånden i denna graf också bevarar avståndet mellan $p$ och $q$ . Den fullständiga Beckman-Quarles-satsen säger att de enda transformationerna av det euklidiska planet (eller ett högre dimensionellt euklidiskt utrymme) som bevarar enhetsavstånd är isometrierna . På motsvarande sätt, för den oändliga enhetsdistansgrafen som genereras av alla punkter i planet, bevarar alla grafautomorfismer alla avstånd i planet, inte bara enhetsavstånden.

Om $\alpha$ är ett algebraiskt tal med modul 1 som inte är en rot till enhet , så bildar heltalskombinationerna av potenser av $\alpha$ en ändligt genererad undergrupp av den additiva gruppen av komplexa tal vars enhetsavståndsgrafen har oändlig grad . Till exempel $\alpha$ väljas som en av de två komplexa rötterna av polynomet $z^{4}-z^{3}- z^{2}-z+1$ , som producerar en oändlig graders enhetsdistansgraf med fyra generatorer.

Färg

Huvudartikel: Hadwiger–Nelson problem

Olöst problem i matematik :

Vilket är det största möjliga kromatiska talet för en enhetsdistansgraf?

(fler olösta problem i matematik)

Hadwiger –Nelson-problemet gäller det kromatiska antalet enhetsavståndsgrafer, och mer specifikt av den oändliga enhetsdistansgrafen som bildas från alla punkter på det euklidiska planet. Enligt de Bruijn-Erdős teorem , som antar valets axiom , motsvarar detta att fråga efter det största kromatiska numret av en graf med ändlig enhetsavstånd. Det finns enhetsdistansgrafer som kräver fem färger i valfri färg, och alla enhetsdistansgrafer kan färgas med högst sju färger.

En sjufärgad av den oändliga enhetsdistansgrafen bildad från alla punkter i planet, och den fyrkromatiska Moser-spindeln inbäddad som en enhetsdistansgraf

För att svara på en annan fråga från Paul Erdős, är det möjligt för triangelfria enhetsdistansgrafer att kräva fyra färger.

Uppräkning

Antalet strikta enhetsdistansgrafer på $n\geq 4$ märkta hörn är som mest

$${\binom {n(n-1)}{2n}}=O\ left(2^{{\bigl (}4+o(1){\bigr )}n\log _{2}n}\höger),$$

uttryckt med stor O-notation och liten o-notation.

Generalisering till högre dimensioner

Definitionen av en enhetsdistansgraf kan naturligtvis generaliseras till vilket euklidiskt utrymme som helst med högre dimensioner . I tre dimensioner har enhetsavståndsgrafer för $n$ punkter som mest $n^{3/2}\beta (n)$ kanter, där $\ beta$ är en mycket långsamt växande funktion relaterad till den omvända Ackermann - funktionen . Detta resultat leder till en liknande gräns för antalet kanter av tredimensionella relativa grannskapsgrafer . I fyra eller fler dimensioner är alla kompletta tvådelade grafer en enhetsavståndsgraf, realiserad genom att placera punkterna på två vinkelräta cirklar med ett gemensamt centrum, så enhetsavståndsgrafer kan vara täta grafer . Uppräkningsformlerna för enhetsdistansgrafer generaliserar till högre dimensioner och visar att i dimension fyra eller fler är antalet strikta enhetsdistansgrafer mycket större än antalet subgrafer av enhetsdistansgrafer.

Vilken finit graf som helst kan vara inbäddad som en enhetsdistansgraf i en tillräckligt hög dimension. Vissa grafer kan behöva mycket olika dimensioner för inbäddningar som icke-strikta enhetsdistansgrafer och som strikta enhetsdistansgrafer. Till exempel $2n$ -vertex krongrafen bäddas in i fyra dimensioner som en icke-strikt enhetsdistansgraf (det vill säga så att alla dess kanter har enhetslängd). Det kräver dock att minst $n-2$ dimensioner är inbäddade som en strikt enhetsdistansgraf, så att dess kanter är de enda enhetsavståndsparen. Dimensionen som krävs för att realisera en given graf som en strikt enhetsgraf är högst dubbelt så mycket som dess maximala grad.

Beräkningskomplexitet

Att konstruera en enhetsavståndsgraf från dess punkter är ett viktigt steg för andra algoritmer för att hitta kongruenta kopior av något mönster i en större punktuppsättning. Dessa algoritmer använder denna konstruktion för att söka efter kandidatpositioner där ett av avstånden i mönstret finns, och använder sedan andra metoder för att testa resten av mönstret för varje kandidat. En metod från Matoušek (1993) kan tillämpas på detta problem, vilket ger en algoritm för att hitta en plan punktuppsättnings enhetsdistansgraf i tiden $n^{4/3} 2^{O(\log ^{*}n)}$ där $\log ^{*}$ är den långsamt växande itererade logaritmfunktionen .

Det är NP-svårt - och mer specifikt komplett för den existentiella teorin om verkligheten - att testa om en given graf är en (strikt eller icke-strikt) enhetsdistansgraf i planet. Det är också NP-komplett att avgöra om en plan enhetsdistansgraf har en Hamiltonsk cykel , även när grafens hörn alla har kända heltalskoordinater.

Källor

•   Ágoston, Péter; Pálvölgyi, Dömötör (april 2022), "An improved constant factor for the unit distance problem", Studia Scientiarum Mathematicarum Hungarica , Akademiai Kiado Zrt., 59 (1): 40–57, arXiv : 2006.06285 , doi : 102012.5.5/02012.5.5. , S2CID 218479287
•    Alon, Noga ; Kupavskii, Andrey (2014), "Two notions of unit distance graphs" (PDF) , Journal of Combinatorial Theory , Series A, 125 : 1–17, doi : 10.1016 /j.jcta.2014.02.006 , MR 6 41274C 9207C 92074C 92024C
•    Beckman, FS; Quarles, DA, Jr. (1953), "On isometries of Euclidian spaces", Proceedings of the American Mathematical Society , 4 (5): 810–815, doi : 10.2307/2032415 , JSTOR 2032415 , MR 005819333
•   Braß, Peter (2002), "Combinatorial geometry problems in pattern recognition", Discrete & Computational Geometry , 28 (4): 495–510, doi : 10.1007/s00454-002-2884-3 , MR 1949897
•    Brouwer, Andries E. ; Haemers, Willem H. (2012), Spectra of Graphs , Universitext, New York: Springer, sid. 178, doi : 10.1007/978-1-4614-1939-6 , ISBN 978-1-4614-1938-9 , MR 2882891
•    Carmi, Paz; Dujmović, Vida ; Morin, Pat ; Wood, David R. (2008), "Distinct distances in graph drawings" , Electronic Journal of Combinatorics , 15 (1): Research Paper 107, arXiv : 0804.3690 , doi : 10.37236/831 , MR 243825082 , S552579 , S.
•   Chan, Timothy M .; Zheng, Da Wei (2022), "Hopcrofts problem, log-star rakning, 2d fraktionerad kaskad och beslutsträd", i Naor, Joseph (Seffi); Buchbinder, Niv (red.), Proceedings of the 2022 ACM-SIAM Symposium on Discrete Algorithms, SODA 2022, Virtual Conference / Alexandria, VA, USA, 9 - 12 januari 2022, Society for Industrial and Applied Mathematics, s. 190– 210, arXiv : 2111.03744 , doi : 10.1137/1.9781611977073.10 , S2CID 243847672
•   Chilakamarri, Kiran B. (1995), "A 4-chromatic unit-distance graph with no triangles", Geombinatorics , 4 (3): 64–76, MR 1313386
•   Chilakamarri, Kiran B.; Mahoney, Carolyn R. (1995), "Maximal and minimal forbidden unit-distance graphs in the plane", Bulletin of the Institute of Combinatorics and Its Applications , 13 : 35–43, MR 1314500 , som citeras av Globus & Parshall (2020) )
•    Clarkson, Kenneth L .; Edelsbrunner, Herbert ; Guibas, Leonidas J .; Sharir, Micha ; Welzl, Emo (1990), "Kombinatoriska komplexitetsgränser för arrangemang av kurvor och sfärer", Discrete & Computational Geometry , 5 ( 2): 99–160, doi : 10.1007/BF02187783 , MR 10324370 28 S124C3ID 98124370
•   de Grey, Aubrey DNJ (2018), "Planets kromatiska nummer är minst 5", Geombinatorics , 28 : 5–18, arXiv : 1804.02385 , MR 3820926
•   Erdős, Paul (1946), "On sets of distances of $n$ points", American Mathematical Monthly , 53 (5): 248–250, doi : 10.2307/2305092 , JSTOR 2305092
•   Erdős, Paul ; Harary, Frank ; Tutte, William T. (1965), " On the dimension of a graph" (PDF) , Mathematika , 12 (2): 118–122, doi : 10.1112 /S0025579300005222 , hdl : 2027.402/15249 1,86049
• Erdős, Paul ; Simonovits, Miklós (1980), "On the chromatic number of geometric graphs", Ars Combinatoria , 9 : 229–246 , som citeras av Soifer (2008 , s. 97)
•    Erdős, Paul (1990), "Några av mina olösta favoritproblem", i Baker, A.; Bollobás, B.; Hajnal, A. (red.), A tribute to Paul Erdős , Cambridge University Press, s. 467–478, ISBN 0-521-38101-0 , MR 1117038 ; se särskilt sid. 475
• Gerbracht, Eberhard H.-A. (2009), Elva enhetsavståndsinbäddningar av Heawood-grafen , arXiv : 0912.5395 , Bibcode : 2009arXiv0912.5395G
• Gervacio, Severino V.; Lim, Yvette F.; Maehara, Hiroshi (2008), "Planar unit-distance graphs with planar unit-distance complement", Discrete Mathematics , 308 (10): 1973–1984, doi : 10.1016/j.disc.2007.04.050
•   Globus, Aidan; Parshall, Hans (2020), "Small unit-distance graphs in the plane", Bulletin of the Institute of Combinatorics and Its Applications , 90 : 107–138, arXiv : 1905.07829 , MR 4156400
•   Griffiths, Martin (juni 2019), "103.27 A property of a particular unit-distance graph", The Mathematical Gazette , 103 (557): 353–356, doi : 10.1017/mag.2019.74 , S2CID 23336195
•   Horvat, Boris; Pisanski, Tomaž (2010), "Products of unit distance graphs", Discrete Mathematics , 310 (12): 1783–1792, doi : 10.1016/j.disc.2009.11.035 , MR 2610282
•    Huson, Mark L.; Sen, Arunabha (1995), "Broadcast scheduling algorithms for radio networks", Military Communications Conference, IEEE MILCOM '95 , vol. 2, s. 647–651, doi : 10.1109/MILCOM.1995.483546 , ISBN 0-7803-2489-7 , S2CID 62039740
•    Itai, Alon; Papadimitriou, Christos H. ; Szwarcfiter, Jayme Luiz (1982), " Hamilton paths in grid graphs", SIAM Journal on Computing , 11 (4): 676–686, CiteSeerX 10.1.1.383.1078 , doi : 10.1105 / 021
• Jaromczyk, Jerzy W.; Toussaint, Godfried T. (1992), "Relative grannskapsgrafer och deras släktingar", Proceedings of the IEEE , 80 (9): 1502–1517, doi : 10.1109/5.163414
• Langin, Katie (18 april 2018), "Amatörmatematiker knäcker årtionden gammalt matematikproblem" , Vetenskap
•    Lavollée, Jérémy; Swanepoel, Konrad J. (2022), "Bounding the number of edges of matchstick graphs", SIAM Journal on Discrete Mathematics , 36 (1): 777–785, arXiv : 2108.07522 , doi : 10.1137/21137/21429 , 0ID 21429 , 0ID 13429 , 0777-785 37142624
• Maehara, Hiroshi (1991), "Distances in a rigid unit-distance graph in the plane", Discrete Applied Mathematics , 31 (2): 193–200, doi : 10.1016/0166-218X(91)90070-D
•   Maehara, Hiroshi (1992), "Extending a flexible unit-bar framework to a rigid one", Discrete Mathematics , 108 (1–3): 167–174, doi : 10.1016/0012-365X(92)90671-2 , MR 1189840
•   Maehara, Hiroshi; Rödl, Vojtech (1990), "On the dimension to represent a graph by a unit distance graph", Graphs and Combinatorics , 6 (4): 365–367, doi : 10.1007/BF01787703 , S2CID 31148911
•   Matoušek, Jiří (1993), "Range searching with efficient hierarchical cuttings", Discrete & Computational Geometry , 10 (2): 157–182, doi : 10.1007/BF02573972 , MR 1220545
•   O'Donnell, Paul (1995), "A 40 vertex 4-chromatic triangle-free unit distance graph", Geombinatorics , 5 (1): 31–34, MR 1337155
•    Pach, János ; Tardos, Gábor (2005), "Förbjudna mönster och enhetsavstånd", i Mitchell, Joseph SB; Rote, Günter (red.), Proceedings of the 21st ACM Symposium on Computational Geometry, Pisa, Italien, 6-8 juni 2005 , Association for Computing Machinery, s. 1–9, doi : 10.1145/1064092.1064092.106400 , MR 244 , MR 296 , 4164092.10640 18752227
•    Radchenko, Danylo (2021), "Unit distance graphs and algebraic integers", Discrete & Computational Geometry , 66 (1): 269–272, doi : 10.1007/s00454-019-00152-4 , hdl : 106/011/06/011/06/011/06/011/011/06/06. 9CFD-E , MR 4270642 , S2CID 119682489
•    Schaefer, Marcus (2013), "Realizability of graphs and linkages", i Pach, János (red.), Thirty Essays on Geometric Graph Theory , Springer, s. 461–482, CiteSeerX 10.1.1.220.9651 , doi : 70/10. 978-1-4614-0110-0_24 , ISBN 978-1-4614-0109-4
•   Soifer, Alexander (2008), The Mathematical Coloring Book , Springer-Verlag, ISBN 978-0-387-74640-1
•    Spencer, Joel ; Szemerédi, Endre ; Trotter, William T. (1984), "Unit distances in the Euclidean plane", i Bollobás, Béla (red.), Graph Theory and Combinatorics , London: Academic Press, s. 293–308, ISBN 978-0-12- 111760-3 , MR 0777185
•   Szemerédi, Endre (2016), "Erdős's unit distance problem", i Nash, John Forbes, Jr .; Rassias, Michael Th. (red.), Open Problems in Mathematics , Cham, Schweiz: Springer, s. 459–477, doi : 10.1007/978-3-319-32162-2_15 , MR 3526946
•    Tyszka, Apoloniusz (2000), "Discrete versions of the Beckman-Quarles theorem", Aequationes Mathematicae , 59 (1–2): 124–133, arXiv : math/9904047 , doi : 10.1007 /1007/110 4C, 4107/4107/4C , 41007/1107 , 41007/4107 14803182
•   Wormald, Nicholas (1979), "A 4-chromatic graph with a special plane drawing", Journal of the Australian Mathematical Society , Series A, 28 ( 1): 1–8, doi : 10.1017/S1446788700014865 , MR 05416CID , S4216ID  
•   Žitnik, Arjana; Horvat, Boris; Pisanski, Tomaž (2012), "All generalized Petersen graphs are unit-distance graphs", Journal of the Korean Mathematical Society , 49 (3): 475–491, doi : 10.4134/JKMS.2012.49.3.475 , MR 295303

externa länkar

• Venkatasubramanian, Suresh, "Problem 39: Distances between Point Sets in R ² and R ³ " , The Open Problems Project
• Weisstein, Eric W. , "Unit-Distance Graph" , MathWorld