Krona graf

Krona graf
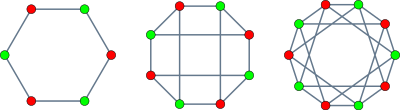Krona grafer med sex, åtta och tio hörn
Vertices	2 n
Kanter	n ( n – 1)
Radie	$\left\{{\begin{array}{ll}\infty &n\leq 2\\3&{\text{annars}}\end{array}}\right.$
Diameter	$\left\{{\begin{array}{ll}\infty &n\leq 2\\3&{\text{annars}}\end{array}}\right.$
Omkrets	$\left\{{\begin{array}{ll}\infty &n\leq 2\\6&n=3\\4&{\text{annars}}\end {array}}\höger.$
Kromatiskt nummer	$\left\{{\begin{array}{ll}1&n=1\\2&{\text{annars}}\end{array}}\right.$
Egenskaper	Distanstransitiv
Notation	$S_{n}^{0}$
Tabell över grafer och parametrar

I grafteorin , en gren av matematiken, är en krongraf på 2 n hörn en oriktad graf med två uppsättningar av hörn { u ₁ , u ₂ , …, u _n } och { v ₁ , v ₂ , …, v _n } och med en kant från u _i till v _j närhelst i ≠ j .

Krongrafen kan ses som en komplett tvådelad graf från vilken kanterna på en perfekt matchning har tagits bort, som det tvådelade dubbla täcket av en fullständig graf , som tensorprodukten K _n × K ₂ , som komplementet till den kartesiska direkten produkt av K _n och K ₂ , eller som en tvådelad Kneser-graf H _{n ,1} som representerar 1-post och ( n – 1) -item-delmängder av en n -postmängd, med en kant mellan två undermängder närhelst en finns i den andra.

Exempel

Krongrafen med 6 vertex bildar en cykel , och krongrafen med 8 vertex är isomorfisk mot grafen för en kub . I Schläfli-dubbelsexan , en konfiguration av 12 linjer och 30 punkter i tredimensionellt utrymme, skär de tolv linjerna varandra i mönstret av en krongraf med 12 vertex.

Egenskaper

Ett biclique-omslag av krongrafen med tio vertex

Antalet kanter i en krongraf är det proniska talet n ( n – 1) . Dess akromatiska nummer är n : man kan hitta en komplett färgning genom att välja varje par { u _i , v _i } som en av färgklasserna. Krondiagram är symmetriska och avståndstransitiva . Archdeacon et al. (2004) beskriver uppdelningar av kanterna på en krongraf i lika långa cykler.

2 n -vertex krongrafen kan vara inbäddad i fyrdimensionell euklidisk rymd på ett sådant sätt att alla dess kanter har enhetslängd. Emellertid kan denna inbäddning också placera några icke-intilliggande hörn på ett enhetsavstånd från varandra. En inbäddning där kanter är på enhetsavstånd och icke-kanter inte på enhetsavstånd kräver minst n – 2 dimensioner. Detta exempel visar att en graf kan kräva mycket olika dimensioner för att representeras som en enhetsdistansgraf och som en strikt enhetsdistansgraf.

Det minsta antalet kompletta tvådelade subgrafer som behövs för att täcka kanterna på en krongraf (dess tvådelade mått eller storleken på ett minsta biclique-omslag) är

$\sigma (n)=\min \left\{\,k\mid n\leq {\binom {k} {\lfloor k/2\rfloor }}\,\right\},$

den inversa funktionen av den centrala binomialkoefficienten .

Komplementgrafen för en krongraf med 2 n -vertex är den kartesiska produkten av kompletta grafer K ₂ ▢ K _n , eller motsvarande 2 × n torns graf .

Ansökningar

Inom etikett är en traditionell regel för att arrangera gäster vid ett middagsbord att män och kvinnor ska byta positioner, och att inga gifta par ska sitta bredvid varandra. Arrangemangen som uppfyller denna regel, för en part som består av n gifta par, kan beskrivas som Hamiltons cykler av en krongraf. Till exempel kan arrangemangen av hörn som visas i figuren tolkas som sitttabeller av denna typ där varje man och hustru sitter så långt ifrån varandra som möjligt. Problemet med att räkna antalet möjliga sittarrangemang, eller nästan likvärdigt antalet Hamilton-cykler i en krona, är känt inom kombinatoriken som ménageproblemet ; för krondiagram med 6, 8, 10, ... hörn är antalet (orienterade) Hamilton-cykler

2, 12, 312, 9600, 416880, 23879520, 1749363840, ... (sekvens A094047 i OEIS )

₀₀ Krongrafer kan användas för att visa att giriga färgningsalgoritmer beter sig dåligt i värsta fall: om hörnpunkterna i en krongraf presenteras för algoritmen i ordningen u , v , u ₁ , v ₁ etc., så blir en girig färgning använder n färger, medan det optimala antalet färger är två. Denna konstruktion tillskrivs Johnson (1974) ; krongrafer kallas ibland Johnsons grafer med notation J _n . Fürer (1995) använder krondiagram som en del av en konstruktion som visar hårdheten för approximation av färgproblem.

Matoušek (1996) använder avstånd i krongrafer som ett exempel på ett metriskt utrymme som är svårt att bädda in i ett normerat vektorrum .

Som Miklavič & Potočnik (2003) visar är krongrafer en av ett litet antal olika typer av grafer som kan förekomma som avståndsregelbundna cirkulationsgrafer .

Agarwal et al. (1994) beskriver polygoner som har krondiagram som sina synlighetsgrafer ; de använder det här exemplet för att visa att det kanske inte alltid är utrymmeseffektivt att representera synlighetsgrafer som sammanslutningar av kompletta tvådelade grafer.

  En krongraf med 2 n hörn, med dess kanter orienterade från den ena sidan av bipartitionen till den andra, utgör standardexemplet på en delvis ordnad uppsättning med ordningsdimension n .

Anteckningar

•   Agarwal, Pankaj K. ; Alon, Noga ; Aronov, Boris ; Suri, Subhash (1994), "Kan synlighetsgrafer representeras kompakt?", Discrete and Computational Geometry , 12 (1): 347–365, doi : 10.1007/BF02574385 , MR 1298916 .
•   Ärkediakon, D. ; Debowsky, M.; Dinitz, J .; Gavlas, H. (2004), "Cycle systems in the complete bipartite graph minus a one-factor", Discrete Mathematics , 284 (1–3): 37–43, doi : 10.1016/j.disc.2003.11.021 , MR 2071894 .
•   Chaudhary, Amitabh; Vishwanathan, Sundar (2001), "Approximation algorithms for the achromatic number", Journal of Algorithms , 41 ( 2): 404–416, CiteSeerX 10.1.1.1.5562 , doi : 10.1006/jagm.19201 , 19201   .
•   de Caen, Dominique ; Gregory, David A.; Pullman, Norman J. (1981), "The Boolean rank of zero-one matrices", i Cadogan, Charles C. (red.), Proc. 3rd Caribbean Conference on Combinatorics and Computing , Institutionen för matematik, University of the West Indies, s. 169–173, MR 0657202 .
•   Erdős, Paul ; Simonovits, Miklós (1980), "Om det kromatiska antalet geometriska grafer" (PDF) , Ars Combinatoria , 9 : 229–246, MR 0582295 .
•   Fürer, Martin (1995), "Förbättrade hårdhetsresultat för att approximera det kromatiska talet", Proc. 36:e IEEE Symp. Foundations of Computer Science (FOCS '95) , s. 414–421, doi : 10.1109/SFCS.1995.492572 , ISBN 978-0-8186-7183-8 .
•   Johnson, DS (1974), "Worst-case behavior of graph coloring algorithms", Proc. 5th Southeastern Conf. on Combinatorics, Graph Theory, and Computing, Utilitas Mathematicae , Winnipeg, s. 513–527, MR 0389644
•    Kubale, M. (2004), Graph Colorings , American Mathematical Society, ISBN 978-0-8218-3458-9 , MR 2074481
•   Matoušek, Jiří (1996), "On the distortion required for embedding finite metric spaces into normed spaces", Israel Journal of Mathematics , 93 (1): 333–344, doi : 10.1007/BF02761110 , MR 1380650 .
•   Miklavič, Štefko; Potočnik, Primož (2003), "Distance-regular circulants", European Journal of Combinatorics , 24 (7): 777–784, doi : 10.1016/S0195-6698(03)00117-3 , MR 2009391 .

externa länkar

• Weisstein, Eric W. "Crown Graph" . MathWorld .