Kaktus graf

En kaktusgraf

Inom grafteorin är en kaktus (kallas ibland ett kaktusträd ) en sammankopplad graf där två enkla cykler som mest har en vertex gemensam. På motsvarande sätt är det en sammankopplad graf där varje kant hör till högst en enkel cykel, eller (för icke-trivial kaktus) där varje block (maximal subgraf utan en cut-vertex ) är en kant eller en cykel.

Egenskaper

Kaktusar är ytterplanära grafer . Varje pseudoträd är en kaktus. En icke-trivial graf är en kaktus om och bara om varje block är antingen en enkel cykel eller en enda kant.

Familjen av grafer där varje komponent är en kaktus stängs nedåt under grafiska mindre operationer. Denna graffamilj kan kännetecknas av en enda förbjuden moll , den fyrkantiga diamantgrafen som bildas genom att ta bort en kant från hela grafen K ₄ .

Triangulär kaktus

Vänskapsgrafer är triangulära kaktusar

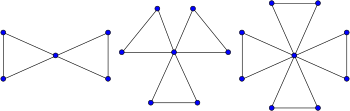
En triangulär kaktus är en speciell typ av kaktusgraf så att varje cykel har längd tre och varje kant tillhör en cykel. Till exempel är vänskapsgraferna , grafer bildade av en samling trianglar som är sammanfogade i en enda delad vertex, triangulära kaktusar. Förutom att de är kaktusgrafer är de triangulära kaktusarna också blockgrafer och lokalt linjära grafer .

Triangulära kaktusar har egenskapen att de förblir anslutna om någon matchning tas bort från dem; för ett givet antal hörn har de minsta möjliga kanter med denna egenskap. Varje träd med ett udda antal hörn kan utökas till en triangulär kaktus genom att lägga till kanter på den, vilket ger en minimal förstärkning med egenskapen att förbli ansluten efter att en matchning tagits bort.

Den största triangulära kaktusen i någon graf kan hittas i polynomtid med hjälp av en algoritm för matroidparitetsproblemet . Eftersom triangulära kaktusgrafer är plana grafer , kan den största triangulära kaktusen användas som en approximation till den största plana subgrafen, ett viktigt delproblem i planarisering . Som en approximationsalgoritm har denna metod approximationsförhållandet 4/9, den mest kända för problemet med maximal plana subgraf.

Algoritmen för att hitta den största triangulära kaktusen är associerad med en sats av Lovász och Plummer som kännetecknar antalet trianglar i denna största kaktus. Lovász och Plummer betraktar par av partitioner av hörn och kanter av den givna grafen i delmängder, med egenskapen att varje triangel i grafen antingen har två hörn i en enda klass av vertexpartitionen eller alla tre kanterna i en enda klass av grafen. kantpartition; de kallar ett par partitioner med den här egenskapen giltig . Då är antalet trianglar i den största triangulära kaktusen lika med maximum, över par av giltiga partitioner ${\mathcal {P}}=\{V_{1} ,V_{2},\dots ,V_{k}\}$ och ${\mathcal {Q}}=\{E_{1},E_ {2},\dots ,E_{m}\}$ , av

$\sum _{i=1}^{m}{\frac {(u_{i}-1)}{2}}+ nk,$ ,

där $n$ är antalet hörn i den givna grafen och $u_{i}$ är antalet vertexklasser som möts av kantklassen $E_{i}$ .

Nyligen bevisades en snäv yttergräns som visade att givet varje ${\displaystyle 1$ graf $G$ finns det alltid en kaktussubgraf $C\subseteq G$ som innehåller minst bråkdel av de triangulära ytorna av $G$ . Detta resultat innebär en direkt analys av 4/9 - approximationsalgoritmen för maximalt plana subgrafproblem utan att använda ovanstående min-max-formel.

Rosas gissning

En viktig gissning relaterad till den triangulära kaktusen är Rosa's Conjecture , uppkallad efter Alexander Rosa , som säger att alla triangulära kaktusar är graciösa eller nästan graciösa. Mer exakt

Alla triangulära kaktusar med t ≡ 0, 1 mod 4 block är graciösa, och de med t ≡ 2, 3 mod 4 är nästan graciösa.

Algoritmer och applikationer

Vissa anläggningslokaliseringsproblem som är NP-svåra för allmänna grafer, liksom vissa andra grafproblem, kan lösas i polynomtid för kaktusar.

Eftersom kaktusar är specialfall av ytterplanära grafer kan ett antal kombinatoriska optimeringsproblem på grafer lösas för dem i polynomtid .

Kaktusar representerar elektriska kretsar som har användbara egenskaper. En tidig applicering av kaktusar var förknippad med representationen av op-amps.

Kaktusar har också använts i jämförande genomik som ett sätt att representera förhållandet mellan olika genom eller delar av genom.

Om en kaktus är ansluten, och var och en av dess hörn hör till högst två block, så kallas den en julkaktus . Varje polyedrisk graf har en julkaktussubgraf som inkluderar alla dess hörn, ett faktum som spelar en viktig roll i ett bevis av Leighton & Moitra (2010) att varje polyedrisk graf har en girig inbäddning i det euklidiska planet , en tilldelning av koordinater till de hörn för vilka girig vidarebefordran lyckas dirigera meddelanden mellan alla par av hörn.

I topologisk grafteori är graferna vars cellulära inbäddningar alla är plana exakt underfamiljen av kaktusgraferna med den ytterligare egenskapen att varje vertex hör till högst en cykel. Dessa grafer har två förbjudna minderåriga, diamantgrafen och vänskapsgrafen med fem hörn .

Historia

Kaktusar studerades först under namnet Husimi-träd , skänkt dem av Frank Harary och George Eugene Uhlenbeck för att hedra tidigare arbete med dessa grafer av Kôdi Husimi . Samma Harary–Uhlenbeck-tidning reserverar namnet "kaktus" för grafer av denna typ där varje cykel är en triangel, men nu är det standard att tillåta cykler av alla längder.

Samtidigt kom namnet Husimi-träd vanligtvis att hänvisa till grafer där varje block är en komplett graf (motsvarande skärningsgraferna för blocken i någon annan graf). Denna användning hade lite att göra med Husimis arbete, och den mer relevanta termen blockgraf används nu för denna familj; men på grund av denna tvetydighet har denna fras blivit mer sällan använd för att hänvisa till kaktusdiagram.

externa länkar

• Tillämpning av kaktusgrafer i analys och design av elektroniska kretsar