Deterministisk finit automat

"DFSA" omdirigerar hit. DFSA kan också hänvisa till narkotika-underlättade sexuella övergrepp .

₀₀₀ Ett exempel på en deterministisk finit automat som endast accepterar binära tal som är multipler av 3. Tillståndet S är både starttillstånd och accepttillstånd. Till exempel leder strängen _{" 1001 "} till tillståndssekvensen S , S1 , S2 , S1 _, S och accepteras därför.

I beräkningsteorin , en gren av teoretisk datavetenskap , en deterministisk finita automat ( DFA ) - även känd som deterministic finite acceptor ( DFA ), deterministic finite-state machine ( DFSM ) eller deterministic finite-state automat ( DFSA ) - är en maskin med ändligt tillstånd som accepterar eller förkastar en given sträng av symboler, genom att köra genom en tillståndssekvens som unikt bestäms av strängen. Deterministisk hänvisar till det unika i beräkningskörningen. På jakt efter de enklaste modellerna för att fånga finita-tillståndsmaskiner Warren McCulloch och Walter Pitts bland de första forskarna som introducerade ett koncept som liknar finita automater 1943.

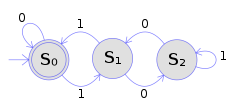
₀₀ Figuren illustrerar en deterministisk finit automat som använder ett tillståndsdiagram . I detta exempel på automat finns det tre tillstånd: S , S ₁ , och S ₂ (betecknas grafiskt med cirklar). Automaten tar en ändlig sekvens av 0:or och 1:or som indata. För varje tillstånd finns det en övergångspil som leder ut till nästa tillstånd för både 0 och 1. Vid läsning av en symbol hoppar en DFA deterministiskt från ett tillstånd till ett annat genom att följa övergångspilen. Till exempel, om automaten för närvarande är i tillstånd S och den aktuella ingångssymbolen är 1, hoppar den deterministiskt till tillstånd _S1 . En DFA har ett starttillstånd (betecknas grafiskt med en pil som kommer in från ingenstans) där beräkningar börjar, och en uppsättning accepterade tillstånd ( betecknas grafiskt med en dubbel cirkel) som hjälper till att definiera när en beräkning är framgångsrik.

En DFA definieras som ett abstrakt matematiskt koncept, men implementeras ofta i hårdvara och mjukvara för att lösa olika specifika problem som lexikal analys och mönstermatchning . En DFA kan till exempel modellera programvara som bestämmer huruvida onlineanvändarinmatning som e-postadresser är syntaktiskt giltiga.

DFA har generaliserats till icke-deterministiska finita automater (NFA) som kan ha flera pilar med samma etikett med början från ett tillstånd. Med hjälp av powerset- konstruktionsmetoden kan varje NFA översättas till en DFA som känner igen samma språk. DFA, och även NFA, känner igen exakt uppsättningen vanliga språk .

Formell definition

En deterministisk finit automat M är en 5- tuppel , ₀ ( Q , Σ, δ , q , F ) , bestående av

• en ändlig uppsättning tillstånd Q
• en ändlig uppsättning ingångssymboler som kallas alfabetet Σ
• en övergångsfunktion δ : Q × Σ → Q
• ett initialt eller starttillstånd $q_{0}\in Q$
• en uppsättning accepterade tillstånd $F\subseteq Q$

Låt w = a ₁ a ₂ … a _n vara en sträng över alfabetet Σ . Automaten M accepterar strängen w om en sekvens av tillstånd, ₀ r , r ₁ , …, r _n , finns i Q med följande villkor:

1. ₀ r = q ₀
2. n r _{i +1} = δ ( ri _, ai _{+1 ,} ) för i = 0, …, − 1
3. $r_{n}\in F$ .

Med ord säger det första villkoret att maskinen startar i starttillståndet q ₀ . Det andra villkoret säger att givet varje tecken i strängen w kommer maskinen att övergå från tillstånd till tillstånd enligt övergångsfunktionen δ . Det sista villkoret säger att maskinen accepterar w om den sista inmatningen av w får maskinen att stanna i ett av de accepterande tillstånden. Annars sägs det att automaten avvisar strängen. Den uppsättning strängar som M accepterar är det språk som M känner igen och detta språk betecknas med L ( M ) .

En deterministisk finit automat utan accepttillstånd och utan starttillstånd kallas ett övergångssystem eller halvautomat .

För en mer omfattande introduktion av den formella definitionen se automatteorin .

Exempel

Följande exempel är en DFA M , med ett binärt alfabet, som kräver att inmatningen innehåller ett jämnt antal nollor.

Tillståndsdiagrammet för M _

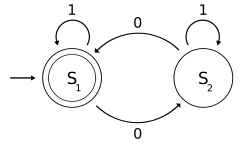
₀ M = ( Q , Σ, 5 , q , F ) där

• Q = { S ₁ , S ₂ }
• Σ = {0, 1}
• ₀ q = S ₁
• F = S1 } _och {
• δ definieras av följande tillståndsövergångstabell :

	0	1
S 1	S 2	S 1
S 2	S 1	S 2

Tillståndet Si _. representerar att det har funnits ett jämnt antal nollor i ingången hittills, medan _S2 betecknar ett udda tal En 1 i ingången ändrar inte automatens tillstånd. När ingången avslutas kommer tillståndet att visa om ingången innehöll ett jämnt antal 0:or eller inte. Om inmatningen innehöll ett jämnt antal 0:or, M att sluta i tillstånd S1 _. , ett accepterande tillstånd, så inmatningssträngen kommer att accepteras

Språket som känns igen av M är det reguljära språket som ges av det reguljära uttrycket (1*) (0 (1*) 0 (1*))* , där * är Kleene-stjärnan , t.ex. 1* anger valfritt tal (eventuellt noll) av på varandra följande.

Variationer

Komplett och ofullständig

Enligt definitionen ovan är deterministiska finita automater alltid kompletta : de definierar från varje tillstånd en övergång för varje ingångssymbol.

Även om detta är den vanligaste definitionen, använder vissa författare termen deterministisk finit automat för en något annorlunda uppfattning: en automat som definierar högst en övergång för varje tillstånd och varje ingångssymbol; övergångsfunktionen tillåts vara partiell . När ingen övergång är definierad stannar en sådan automat.

Lokala automater

En lokal automat är en DFA, inte nödvändigtvis komplett, för vilken alla kanter med samma etikett leder till en enda vertex. Lokala automater accepterar klassen av lokala språk , de för vilka medlemskapet i ett ord i språket bestäms av ett "glidande fönster" med längden två på ordet.

En Myhill-graf över ett alfabet A är en riktad graf med vertexuppsättning A och delmängder av hörn märkta "start" och "finish". Språket som accepteras av en Myhill-graf är uppsättningen av riktade vägar från ett startpunkt till ett slutpunkt: grafen fungerar alltså som en automat. Klassen av språk som accepteras av Myhill-grafer är klassen av lokala språk.

Slumpmässighet

När starttillståndet och accepttillstånden ignoreras, kan en DFA med n tillstånd och ett alfabet av storleken k ses som en digraf av n hörn där alla hörn har k utbågar märkta 1, …, k (a k -out ) digraf). Det är känt att när k ≥ 2 är ett fixerat heltal, med hög sannolikhet, är den största starkt anslutna komponenten (SCC) i en sådan k -out-digraf vald likformigt slumpmässigt av linjär storlek och den kan nås av alla hörn. Det har också bevisats att om k tillåts öka när n ökar, så har hela digrafen en fasövergång för stark anslutning liknande Erdős–Rényi-modellen för anslutning.

I en slumpmässig DFA är det maximala antalet hörn som kan nås från en vertex mycket nära antalet hörn i den största SCC med hög sannolikhet. Detta gäller också för den största inducerade subdigrafen med minsta i grad ett, som kan ses som en riktad version av 1 -kärna .

Stängningsegenskaper

Den övre vänstra automaten känner igen språket för alla binära strängar som innehåller minst en förekomst av "00". Den nedre högra automaten känner igen alla binära strängar med ett jämnt antal "1". Den nedre vänstra automaten erhålls som en produkt av de två förstnämnda, den känner igen skärningspunkten mellan båda språken.

Om DFA:er känner igen språken som erhålls genom att tillämpa en operation på de igenkännbara DFA-språken, sägs DFA:er vara stängda under operationen. DFA:erna är stängda under följande operationer.

• Union
• Korsning (se bild)
• Sammankoppling
• Komplement
• Kleene stängning
• Omkastning
• Kvotient
• Ersättning
• Homomorfism

För varje operation har en optimal konstruktion med hänsyn till antalet tillstånd bestämts i statlig komplexitetsforskning. Eftersom DFA är ekvivalenta med icke-deterministiska finita automater (NFA), kan dessa stängningar också bevisas med hjälp av stängningsegenskaper hos NFA.

Som en övergångsmonoid

En körning av en given DFA kan ses som en sekvens av kompositioner av en mycket allmän formulering av övergångsfunktionen med sig själv. Här konstruerar vi den funktionen.

För en given ingångssymbol $a\in \Sigma$ , kan man konstruera en övergångsfunktion $\delta _{a}:Q\högerpil Q$ genom att definiera $\delta _{a}(q)=\delta (q,a)$ för alla $q\in Q$ . (Detta trick kallas currying .) Ur detta perspektiv " verkar" ${\displaystyle \delta _{a}} på ett tillstånd i Q för att ge ett annat tillstånd.$ Man kan då överväga resultatet av funktionssammansättningen som upprepade gånger tillämpas på de olika funktionerna ${\displaystyle \delta _{a}} ,$ δ $\displaystyle \delta _{b}}$ och så vidare. Givet ett par bokstäver $a,b\in \Sigma$ , kan man definiera en ny funktion ${\widehat {\delta }}_ {ab}=\delta _{a}\circ \delta _{b}$ , där $\circ$ anger funktionssammansättning.

Uppenbarligen kan denna process fortsätta rekursivt, vilket ger följande rekursiva definition av ${\widehat {\delta }}:Q\times \Sigma ^{\star }\rightarrow Q$ :

${\widehat {\delta }}(q,\epsilon )=q$ , där $\epsilon$ är den tomma strängen och

${\widehat {\delta }}(q,wa)=\delta _{a}({\widehat {\delta }}(q,w) )$ , där $w\in \Sigma ^{*},a\in \Sigma$ och $q\in Q$ .

${\widehat {\delta }}$ definieras för alla ord $w\in \Sigma ^{*}$ . En körning av DFA är en sekvens av kompositioner av ${\widehat {\delta }}$ med sig själv.

Upprepad funktionssammansättning bildar en monoid . För övergångsfunktionerna är denna monoid känd som övergångsmonoiden, eller ibland transformationshalvgruppen . Konstruktionen kan också vändas: givet en ${\widehat {\delta }}$ , kan man rekonstruera en $\delta$ , och så är de två beskrivningarna ekvivalenta.

Fördelar och nackdelar

DFA är en av de mest praktiska beräkningsmodellerna, eftersom det finns en trivial linjär tid, konstant rymd, onlinealgoritm för att simulera en DFA på en ström av indata. Det finns också effektiva algoritmer för att hitta en DFA som känner igen:

• komplementet till språket som känns igen av en given DFA.
• föreningen/korsningen av språken som erkänns av två givna DFA:er.

Eftersom DFA:er kan reduceras till en kanonisk form ( minimala DFAs ), finns det också effektiva algoritmer för att bestämma:

• om en DFA accepterar några strängar (Emptiness Problem)
• om en DFA accepterar alla strängar (universitetsproblem)
• om två DFA:er känner igen samma språk (jämlikhetsproblem)
• om språket som erkänns av en DFA ingår i språket som erkänns av en andra DFA (inkluderingsproblem)
• DFA med ett minsta antal tillstånd för ett visst reguljärt språk (Minimeringsproblem)

DFA:er är likvärdiga i beräkningskraft med icke-deterministiska finita automater ( NFA). Detta beror på att för det första är vilken DFA som helst också en NFA, så en NFA kan göra vad en DFA kan göra. Dessutom, givet en NFA, med hjälp av powerset-konstruktionen kan man bygga en DFA som känner igen samma språk som NFA, även om DFA kan ha ett exponentiellt större antal tillstånd än NFA. Men även om NFA:er är beräkningsmässigt likvärdiga med DFA:er, är de ovan nämnda problemen inte nödvändigtvis lösta effektivt även för NFA:er. Problemet med icke-universalitet för NFA:er är PSPACE komplett eftersom det finns små NFA:er med kortast avvisande ord i exponentiell storlek. En DFA är universell om och endast om alla delstater är sluttillstånd, men detta gäller inte för NFA. Problemen med jämställdhet, inkludering och minimering är också PSPACE kompletta eftersom de kräver att de utgör komplementet till en NFA vilket resulterar i en exponentiell sprängning av storlek.

Å andra sidan har finita-tillståndsautomater strikt begränsad kraft i de språk de kan känna igen; många enkla språk, inklusive alla problem som kräver mer än konstant utrymme för att lösa, kan inte kännas igen av en DFA. Det klassiska exemplet på ett enkelt beskrivet språk som ingen DFA kan känna igen är parentes eller Dyck language , dvs språket som består av korrekt parade parenteser som ordet "(()())". Intuitivt kan ingen DFA känna igen Dyck-språket eftersom DFA:er inte kan räknas: en DFA-liknande automat måste ha ett tillstånd för att representera alla möjliga antal "för närvarande öppna" parenteser, vilket innebär att den skulle behöva ett obegränsat antal tillstånd. Ett annat enklare exempel är språket som består av strängar av formen a ⁿ b ⁿ för något ändligt men godtyckligt antal a :n, följt av lika många b :n.

DFA-identifiering från märkta ord

Huvudartikel: Induktion av reguljära språk

Givet en uppsättning positiva ord $S^{+}\subset \Sigma ^{*}$ och en uppsättning negativa ord $S^{-}\subset \ Sigma ^{*}$ man kan konstruera en DFA som accepterar alla ord från $S^{+}$ och avvisar alla ord från $S^{-}$ : detta problem kallas DFA-identifikation (syntes, lärande). Även om vissa DFA kan konstrueras i linjär tid, är problemet med att identifiera en DFA med det minimala antalet tillstånd NP-komplett. Den första algoritmen för minimal DFA-identifiering har föreslagits av Trakhtenbrot och Barzdin i och kallas TB-algoritmen . TB-algoritmen antar dock att alla ord från $\Sigma$ upp till en given längd finns i antingen $S^{+}\cup S^{-}$ .

Senare föreslog K. Lang en förlängning av TB-algoritmen som inte använder några antaganden om $S^{+}$ och $S^{-}$ Traxbar - algoritmen . Traxbar garanterar dock inte minimaliteten hos den konstruerade DFA. I sitt arbete föreslog EM Gold också en heuristisk algoritm för minimal DFA-identifiering. Golds algoritm antar att $S^{+}$ och $S^{-}$ innehåller en karakteristisk uppsättning av det vanliga språket; annars kommer den konstruerade DFA:n att vara inkonsekvent antingen med $S^{+}$ eller $S^{-}$ . Andra anmärkningsvärda DFA-identifieringsalgoritmer inkluderar RPNI-algoritmen, Blue-Fringe evidensdriven tillståndssammanslagningsalgoritm, Windowed-EDSM. En annan forskningsriktning är tillämpningen av evolutionära algoritmer : den evolutionära algoritmen för märkning av smarta tillstånd tillåts lösa ett modifierat DFA-identifieringsproblem där träningsdata (sätter $S^{+}$ och $S^ {-}$ ) är bullrig i den meningen att vissa ord hänförs till fel klasser.

Ytterligare ett steg framåt beror på tillämpningen av SAT- lösare av Marjin JH Heule och S. Verwer: det minimala DFA-identifieringsproblemet reduceras till att avgöra om en boolesk formel är tillfredsställande. Huvudidén är att bygga en förstärkt prefix-trädacceptor (ett försök som innehåller alla inmatningsord med motsvarande etiketter) baserat på inmatningsmängderna och minska problemet med att hitta en DFA med $C$ tillstånd till att färga trädets hörn med $C$ anger på ett sådant sätt att när hörn med en färg slås samman till ett tillstånd, är den genererade automaten deterministisk och överensstämmer med $S^{+}$ och $S^ {-}$ . Även om detta tillvägagångssätt tillåter att hitta den minimala DFA, lider det av exponentiell sprängning av exekveringstid när storleken på indata ökar. Därför har Heule och Verwers initiala algoritm senare utökats med att göra flera steg av EDSM-algoritmen innan SAT-lösaren körs: DFASAT-algoritmen. Detta gör det möjligt att minska sökutrymmet för problemet, men leder till förlust av minimalitetsgarantin. Ett annat sätt att minska sökutrymmet har föreslagits med hjälp av nya symmetribrytande predikat baserade på bredd- först-sökalgoritmen : de sökta DFA:s tillstånd är begränsade till att numreras enligt BFS-algoritmen som startas från det initiala tillståndet. Detta tillvägagångssätt minskar sökutrymmet med $C!$ genom att eliminera isomorfa automater.

Motsvarande modeller

Läsbara högerrörliga Turing-maskiner

Läsbara högerrörliga Turing-maskiner är en speciell typ av Turing-maskin som bara rör sig åt höger; dessa motsvarar nästan exakt DFA. Definitionen baserad på ett enskilt oändligt band är ] en 7- tupel

$M=\langle Q,\Gamma ,b,\Sigma ,\delta ,q_{0},F\rangle ,$

var

$Q$ är en ändlig uppsättning tillstånd ;

$\Gamma$ är en ändlig uppsättning av bandalfabetet/symbolerna ;

$b\in \Gamma$ är den tomma symbolen (den enda symbol som får förekomma på bandet oändligt ofta i vilket steg som helst under beräkningen);

$\Sigma$ , en delmängd av $\Gamma$ inklusive b , är uppsättningen av ingångssymboler ;

$\delta :Q\times \Gamma \to Q\times \Gamma \times \{R\}$ är en funktion som kallas övergångsfunktionen , R är en höger rörelse (ett högerskifte);

$q_{0}\in Q$ är initialtillståndet ;

$F\subseteq Q$ är uppsättningen av slutliga eller accepterande tillstånd .

Maskinen accepterar alltid ett vanligt språk. Det måste finnas minst ett element i uppsättningen F (ett HALT- tillstånd) för att språket ska vara tomt.

Exempel på en 3-tillstånd, 2-symbol skrivskyddad Turing-maskin

	Nuvarande tillstånd A			Nuvarande tillstånd B			Nuvarande tillstånd C
tejpsymbol	Skriv symbol	Flytta bandet	Nästa stat	Skriv symbol	Flytta bandet	Nästa stat	Skriv symbol	Flytta bandet	Nästa stat
0	1	R	B	1	R	A	1	R	B
1	1	R	C	1	R	B	1	N	STANNA

$Q=\{A,B,C,{\text{HALT}}\};$

$\Gamma =\{0,1\};$

$b=0$ , "tom";

$\Sigma =\varnothing$ , tom uppsättning;

$\delta =$ se tillståndstabell ovan;

$q_{0}=A$ , initialtillstånd;

$F=$ den ena elementuppsättningen av sluttillstånd: $\{{\text{HALT}}\}$ .

Se även

• Deterministisk acyklisk finita tillståndsautomat
• DFA-minimering
• Monadisk andra ordningens logik
• Powerset konstruktion
• Kvant finit automat
• Problem med att separera ord
• Turing maskin
• Tvåvägs finit automat
• Viktad automat

Anteckningar

•   Hopcroft, John E .; Motwani, Rajeev ; Ullman, Jeffrey D. (2001). Introduktion till automatteori, språk och beräkningar (2 uppl.). Addison Wesley . ISBN 0-201-44124-1 . Hämtad 19 november 2012 .
•    Lawson, Mark V. (2004). Finita automater . Chapman och Hall/CRC. ISBN 1-58488-255-7 . Zbl 1086.68074 .
•   McCulloch, WS; Pitts, W. (1943). "En logisk beräkning av idéerna som finns i nervös aktivitet". Bulletin of Mathematical Biophysics . 5 (4): 115–133. doi : 10.1007/BF02478259 . PMID 2185863 .
• Rabin, MO; Scott, D. (1959). "Finita automater och deras beslutsproblem" . IBM J. Res. Dev . 3 (2): 114–125. doi : 10.1147/rd.32.0114 .
•    Sakarovitch, Jacques (2009). Element i automatteorin . Översatt från franskan av Reuben Thomas. Cambridge: Cambridge University Press . ISBN 978-0-521-84425-3 . Zbl 1188.68177 .
•   Sipser, Michael (1997). Introduktion till teorin om beräkning . Boston: PWS. ISBN 0-534-94728-X . . Avsnitt 1.1: Finite Automata, s. 31–47. Underavsnitt "Beslutbara problem rörande vanliga språk" i avsnitt 4.1: Avgörbara språk, s. 152–155.4.4 DFA kan endast acceptera reguljärt språk