Boolesk tillfredsställelseproblem

Inom logik och datavetenskap är det booleska tillfredsställbarhetsproblemet (ibland kallat propositionellt tillfredsställande problem och förkortat SATISFIABILITY , SAT eller B-SAT ) problemet med att avgöra om det finns en tolkning som uppfyller en given boolesk formel . Med andra ord frågar den om variablerna i en given boolesk formel konsekvent kan ersättas med värdena TRUE eller FALSE på ett sådant sätt att formeln utvärderas till TRUE. Om så är fallet kallas formeln satisfiable . Å andra sidan, om ingen sådan tilldelning finns, är funktionen som uttrycks av formeln FALSK för alla möjliga variabeltilldelningar och formeln är otillfredsställande . Till exempel är formeln " a OCH INTE b " tillfredsställbar eftersom man kan hitta värdena a = TRUE och b = FALSE, vilket gör ( a AND NOT b ) = TRUE. Däremot är " a AND NOT a " otillfredsställande.

SAT är det första problemet som visade sig vara NP-komplett ; se Cook–Levins sats . Det betyder att alla problem i komplexitetsklassen NP , som inkluderar ett brett spektrum av naturliga besluts- och optimeringsproblem, på sin höjd är lika svåra att lösa som SAT. Det finns ingen känd algoritm som effektivt löser varje SAT-problem, och det anses allmänt att ingen sådan algoritm existerar; Ändå har denna övertygelse inte bevisats matematiskt, och att lösa frågan om SAT har en polynom- tidsalgoritm är ekvivalent med P kontra NP-problemet , som är ett berömt öppet problem inom datorteorin.

Ändå, från och med 2007, kan heuristiska SAT-algoritmer lösa probleminstanser som involverar tiotusentals variabler och formler som består av miljontals symboler, vilket är tillräckligt för många praktiska SAT-problem från t.ex. artificiell intelligens , kretsdesign och automatisk teorem som bevisar .

Definitioner

En propositionell logisk formel , även kallad booleskt uttryck , är byggd av variabler , operatorer AND ( konjunktion , även betecknad med ∧), OR ( disjunktion , ∨), NOT ( negation , ¬) och parenteser. En formel sägs vara tillfredsställbar om den kan göras TRUE genom att tilldela lämpliga logiska värden (dvs. TRUE, FALSE) till dess variabler. Det booleska satisfiability-problemet (SAT) är, givet en formel, för att kontrollera om det är tillfredsställbart. Detta beslutsproblem är av central betydelse inom många områden inom datavetenskap , inklusive teoretisk datavetenskap , komplexitetsteori , algoritmik , kryptografi och artificiell intelligens . ^{[ ytterligare citat behövs ]}

Konjunktiv normalform

En literal är antingen en variabel (i vilket fall den kallas positiv literal ) eller negationen av en variabel (kallad negativ literal ). En klausul är en disjunktion av bokstaver (eller en enda bokstavlig). En sats kallas en hornsats om den innehåller högst en positiv bokstavlig. En formel är i konjunktiv normalform (CNF) om den är en konjunktion av satser (eller en enstaka sats). Till exempel $x 1$ en positiv bokstav, $\neg x 2$ är en negativ bokstav, $x 1 \lor \neg x 2$ är en sats. Formeln $(x 1 \lor \neg x 2) \land (\neg x 1 \lor x 2 \lor x 3) \land \neg x 1$ är i konjunktiv normalform; dess första och tredje sats är Horn-satser, men dess andra sats är det inte. Formeln är tillfredsställbar genom att välja x ₁ = FALSK, x ₂ = FALSK och x ₃ godtyckligt, eftersom (FALSE ∨ ¬FALSE) ∧ (¬FALSE ∨ FALSE ∨ x ₃ ) ∧ ¬FALSE ∧ ∨ FALSE utvärderas till (FALSE) (TRUE ∨ FALSE ∨ x ₃ ) ∧ TRUE, och i sin tur till TRUE ∧ TRUE ∧ TRUE (dvs. till TRUE). Däremot är CNF-formeln a ∧ ¬ a , bestående av två satser av en bokstavlig, otillfredsställbar, eftersom den för en =TRUE eller en =FALSE utvärderas till TRUE ∧ ¬TRUE (dvs. FALSE) eller FALSE ∧ ¬FALSE (dvs. , återigen FALSK), respektive.

För vissa versioner av SAT-problemet är det användbart att definiera begreppet en generaliserad konjunktiv normalformformel, dvs. som en konjunktion av godtyckligt många generaliserade satser , den senare är av formen $R (l 1,..., l n)$ för någon boolesk funktion R och (vanliga) bokstaver $l i$ . Olika uppsättningar tillåtna booleska funktioner leder till olika problemversioner. Som ett exempel R (¬ x , a , b ) en generaliserad sats och R (¬ x , a , b ) ∧ R ( b , y , c ) ∧ R ( c , d ,¬ z ) är en generaliserad konjunktiv normalform. Den här formeln används nedan , där R är den ternära operatorn som är TRUE precis när exakt ett av dess argument är det.

boolesk algebras lagar kan varje propositionell logikformel omvandlas till en ekvivalent konjunktiv normalform, som dock kan vara exponentiellt längre. Till exempel, omvandling av formeln ( x ₁ ∧ y ₁ ) ∨ ( x ₂ ∧ y ₂ ) ∨ ... ∨ ( x _n ∧ y _n ) till konjunktiv normalform ger

(x 1 \lor x 2 \lor \dots \lor x n) \land

(y 1 \lor x 2 \lor \dots \lor x n) \land

(( \lor y 1 \lor \lor y 12) \land ... \land

x 1 \lor y 2 \lor \dots \lor x n) \land

(x 1 \lor x 2 \lor \dots \lor n) \land

y (\dots \lor \lor 2 \lor \dots \lor y n)

;

y 1 \lor x 2 \lor \lor y n) \land

(x 1 \lor y 2 \dots y n)

medan den förra är en disjunktion av n konjunktioner av 2 variabler, den senare består av 2 ⁿ satser av n variabler.

Men med användning av Tseytin-transformationen kan vi hitta en ekvisatisfiable konjunktiv normalformformel med längd linjär i storleken på den ursprungliga propositionslogiska formeln.

Komplexitet

SAT var det första kända NP-kompletta problemet, vilket bevisades av Stephen Cook vid University of Toronto 1971 och oberoende av Leonid Levin vid Ryska vetenskapsakademin 1973. Fram till den tidpunkten fungerade inte konceptet med ett NP-komplett problem. till och med existerar. Beviset visar hur varje beslutsproblem i komplexitetsklassen NP kan reduceras till SAT-problemet för CNF-formler, ibland kallat CNFSAT . En användbar egenskap hos Cooks reduktion är att den bevarar antalet accepterande svar. Till exempel, att bestämma om en given graf har en 3-färgning är ett annat problem i NP; om en graf har 17 giltiga 3-färger, kommer SAT-formeln som produceras av Cook–Levin-reduktionen att ha 17 tillfredsställande tilldelningar.

NP-fullständighet avser endast körtiden för de värsta fallen. Många av de fall som uppstår i praktiska tillämpningar kan lösas mycket snabbare. Se Algoritmer för att lösa SAT nedan.

3-tillfredsställelse

3-SAT-instansen

(x \lor x \lor y) \land (\neg x \lor \neg y \lor \neg y) \land (\neg x \lor y \lor y)

reducerad till ett klickproblem . De gröna hörnen bildar en 3-klick och motsvarar den tillfredsställande uppgiften x =FALSK, y =TRUE.

Liksom tillfredsställbarhetsproblemet för godtyckliga formler, är bestämning av tillfredsställbarheten för en formel i konjunktiv normalform där varje sats är begränsad till högst tre bokstaver också NP-komplett; detta problem kallas 3-SAT , 3CNFSAT eller 3-satisfiability . För att reducera det obegränsade SAT-problemet till 3-SAT, transformera varje sats $l 1 \lor \dots \lor l n$ till en konjunktion av $n - 2$ satser

(l 1 \lor l 2 \lor x 2) \land

(\neg x 2 \lor l 3 \lor x 3) \land

((\neg x n - 3 \lor x n - 3 \lor n - 2) \land

\neg x 3 \lor l 4 \lor x 4) \land \dots \land

(\neg x n - 2 \lor l n - 1 \lor l n)

där $x 2, \dots , x n - 2$ är färska variabler som inte förekommer någon annanstans. Även om de två formlerna inte är logiskt ekvivalenta , är de likvärdiga . Formeln som blir resultatet av att transformera alla satser är högst 3 gånger så lång som dess ursprungliga, dvs längdtillväxten är polynom.

3-SAT är ett av Karps 21 NP-kompletta problem , och det används som utgångspunkt för att bevisa att andra problem också är NP-hårda . Detta görs genom polynom-tidsreduktion från 3-SAT till det andra problemet. Ett exempel på ett problem där denna metod har använts är klickproblemet : givet en CNF-formel som består av c- satser, består motsvarande graf av en vertex för varje bokstavlig och en kant mellan varje två icke-motsägande bokstaver från olika satser, jfr. bild. Grafen har en c -klick om och endast om formeln är tillfredsställbar.

Det finns en enkel randomiserad algoritm på grund av Schöning (1999) som löper i tiden (4/3) ⁿ där n är antalet variabler i 3-SAT propositionen, och lyckas med hög sannolikhet att korrekt bestämma 3-SAT.

Den exponentiella tidshypotesen hävdar att ingen algoritm kan lösa 3-SAT (eller faktiskt k -SAT för valfri $k>2$ ) i $exp(o (n))$ tid (dvs. fundamentalt snabbare än exponentiell i n) ).

Selman, Mitchell och Levesque (1996) ger empiriska data om svårigheten med slumpmässigt genererade 3-SAT-formler, beroende på deras storleksparametrar. Svårighetsgraden mäts i antal rekursiva samtal som görs av en DPLL-algoritm . De identifierade en fasövergångsregion från nästan säkert tillfredsställande till nästan säkert otillfredsställande formler vid förhållandet mellan klausuler och variabler vid cirka 4,26.

3-tillfredsställelse kan generaliseras till k-tillfredsställelse ( k-SAT , även k-CNF-SAT ), när formler i CNF beaktas med varje sats som innehåller upp till k literaler. ^{[ citat behövs ]} Men eftersom för alla k ≥ 3 kan detta problem varken vara lättare än 3-SAT eller svårare än SAT, och de två sistnämnda är NP-kompletta, så det måste vara k-SAT.

Vissa författare begränsar k-SAT till CNF-formler med exakt k literaler . ^{[ citat behövs ]} Detta leder inte till en annan komplexitetsklass heller, eftersom varje sats $l 1 \lor \dots \lor l j$ med j < k literaler kan fyllas med fasta dummyvariabler till $l 1 \lor \dots \lor l j \lor d j + 1 \lor \dots \lor d k$ . Efter utfyllnad av alla satser måste 2 ^{k -1 extra satser läggas till för att säkerställa att endast} $d 1 = \dots = d k =FALSK$ kan leda till en tillfredsställande tilldelning. Eftersom k inte beror på formelns längd leder de extra satserna till en konstant ökning av längden. Av samma anledning spelar det ingen roll om duplicerade bokstaver är tillåtna i satser, som i $\neg x \lor \neg y \lor \neg y$ .

Särskilda fall av SAT

Konjunktiv normalform

Konjunktiv normalform (särskilt med 3 bokstaver per sats) anses ofta vara den kanoniska representationen för SAT-formler. Som visas ovan reduceras det allmänna SAT-problemet till 3-SAT, problemet med att bestämma tillfredsställelse för formler i denna form.

Disjunktiv normalform

SAT är trivialt om formlerna är begränsade till de i disjunktiv normalform , det vill säga de är en disjunktion av konjunktioner av bokstavliga ord. En sådan formel är verkligen tillfredsställbar om och endast om minst en av dess konjunktioner är tillfredsställbar, och en konjunktion är tillfredsställbar om och endast om den inte innehåller både x och INTE x för någon variabel x . Detta kan kontrolleras i linjär tid. Dessutom, om de är begränsade till att vara i full disjunktiv normalform , där varje variabel förekommer exakt en gång i varje konjunktion, kan de kontrolleras i konstant tid (varje konjunktion representerar en tillfredsställande tilldelning). Men det kan ta exponentiell tid och utrymme att konvertera ett allmänt SAT-problem till disjunktiv normalform; för ett exempel byt ut "∧" och "∨" i ovanstående exponentiella uppblåsningsexempel mot konjunktiva normala former.

Exakt-1 3-tillfredsställelse

Vänster: Schäfers reduktion av en 3-SAT-sats x ∨ y ∨ z . Resultatet av R är TRUE (1) om exakt ett av dess argument är TRUE, och FALSE (0) annars. Alla 8 kombinationer av värden för x , y , z undersöks, en per rad. De färska variablerna a ,..., f kan väljas för att uppfylla alla satser (exakt ett grönt argument för varje R ) på alla rader utom den första, där x ∨ y ∨ z är FALSK. Höger: En enklare reduktion med samma egenskaper.

En variant av problemet med 3-tillfredsställelse är en-av-tre 3-SAT (även känd på olika sätt som 1-i-3-SAT och exakt-1 3-SAT ). Givet en konjunktiv normalform med tre bokstaver per sats, är problemet att avgöra om det finns en sanningstilldelning till variablerna så att varje sats har exakt en SANT bokstavlig (och därmed exakt två FALSKA bokstaver). Däremot kräver vanlig 3-SAT att varje sats har minst en TRUE bokstavlig. Formellt ges ett ett-av-tre 3-SAT-problem som en generaliserad konjunktiv normalform med alla generaliserade satser som använder en ternär operator R som är SANT bara om exakt ett av dess argument är det. När alla bokstaver i en en-av-tre 3-SAT-formel är positiva kallas tillfredsställbarhetsproblemet en-av-tre positiv 3-SAT .

En av tre 3-SAT, tillsammans med dess positiva fall, listas som NP-komplett problem "LO4" i standardreferensen, Computers and Intractability: A Guide to the Theory of NP-Completeness av Michael R. Garey och David S. Johnson . En-av-tre 3-SAT visade sig vara NP-komplett av Thomas Jerome Schaefer som ett specialfall av Schaefers dikotomisats , som hävdar att alla problem som generaliserar Boolesk tillfredsställelse på ett visst sätt är antingen i klassen P eller är NP- komplett.

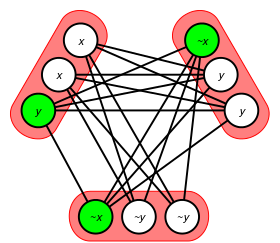
Schaefer ger en konstruktion som tillåter en enkel polynom-tidsreduktion från 3-SAT till en-av-tre 3-SAT. Låt "( x eller y eller z )" vara en sats i en 3CNF-formel. Lägg till sex nya booleska variabler a , b , c , d , e och f , som ska användas för att simulera denna sats och ingen annan. Då är formeln R ( x , a , d ) ∧ R ( y , b , d ) ∧ R ( a , b , e ) ∧ R ( c , d , f ) ∧ R ( z , c , FALSE ) tillfredsställbar med någon inställning av de färska variablerna om och endast om minst en av x , y eller z är TRUE, se bild (vänster). Således kan vilken 3-SAT-instans som helst med m- satser och n variabler konverteras till en likvärdig en-av-tre 3-SAT-instans med 5 m -satser och n +6 m variabler. En annan reduktion involverar endast fyra färska variabler och tre satser: R (¬ x , a , b ) ∧ R ( b , y , c ) ∧ R( c , d ,¬ z ), se bild (höger).

Inte-alla-lika 3-tillfredsställelse

En annan variant är problemet med inte alla lika 3-tillfredsställelse (även kallat NAE3SAT ). Givet en konjunktiv normalform med tre bokstaver per sats, är problemet att avgöra om en tilldelning till variablerna existerar så att i ingen sats alla tre bokstaver har samma sanningsvärde. Detta problem är också NP-komplett, även om inga negationssymboler tillåts, enligt Schaefers dikotomisats.

Linjär SAT

En 3-SAT-formel är Linjär SAT ( LSAT ) om varje sats (sett som en uppsättning bokstaver) skär högst en annan sats, och dessutom, om två satser skär varandra, så har de exakt en bokstavlig gemensamhet. En LSAT-formel kan avbildas som en uppsättning osammanhängande halvslutna intervall på en linje. Att avgöra om en LSAT-formel är tillfredsställande är NP-komplett.

2-tillfredsställelse

SAT är lättare om antalet bokstaver i en sats begränsas till högst 2, i vilket fall problemet kallas 2-SAT . Detta problem kan lösas i polynomtid och är faktiskt komplett för komplexitetsklassen NL . Om dessutom alla OR-operationer i bokstaver ändras till XOR- operationer kallas resultatet exklusiv-eller 2-tillfredsställelse , vilket är ett komplett problem för komplexitetsklassen SL = L .

Horn-tillfredsställelse

Problemet med att bestämma tillfredsställelsen av en given konjunktion av Horn-satser kallas Horn-satisfiability eller HORN-SAT . Det kan lösas i polynomtid med ett enda steg av enhetsutbredningsalgoritmen , som producerar den enda minimala modellen av uppsättningen av Horn-satser (med den uppsättning bokstaver som är tilldelade TRUE). Horn-tillfredsställelse är P-komplett . Det kan ses som P:s version av det booleska tillfredsställbarhetsproblemet. Att avgöra sanningen i kvantifierade Horn-formler kan också göras i polynomtid.

Hornsatser är av intresse eftersom de kan uttrycka implikationen av en variabel från en uppsättning andra variabler. En sådan sats ¬ x ₁ ∨ ... ∨ ¬ x _n ∨ y kan faktiskt skrivas om till x ₁ ∧ ... ∧ x _n → y , det vill säga om x ₁ ,..., x _n alla är SANT , då måste y också vara SANT.

En generalisering av klassen av Horn-formler är den för formler som kan ändras till Horn, vilket är den uppsättning formler som kan placeras i Horn-form genom att ersätta vissa variabler med deras respektive negation. Till exempel, ( x ₁ ∨ ¬ x ₂ ) ∧ (¬ x ₁ ∨ x ₂ ∨ x ₃ ) ∧ ¬ x ₁ är inte en Horn-formel, men kan döpas om till Horn-formeln ( x ₁ ∨ ¬ x ₂ ) ∧ (¬ x ₁ ∨ x ₂ ∨ ¬ y ₃ ) ∧ ¬ x ₁ genom att introducera y ₃ som negation av x ₃ . Däremot leder inget namnbyte av ( x ₁ ∨ ¬ x ₂ ∨ ¬ x ₃ ) ∧ (¬ x ₁ ∨ x ₂ ∨ x ₃ ) ∧ ¬ x ₁ till en Horn-formel. Att kontrollera förekomsten av en sådan ersättning kan göras i linjär tid; därför är tillfredsställbarheten av sådana formler i P eftersom det kan lösas genom att först utföra denna ersättning och sedan kontrollera tillfredsställelsen av den resulterande Horn-formeln.

En formel med 2 satser kan vara missnöjd (röd), 3-nöjd (grön), xor-3-nöjd (blå) eller/och 1-i-3-nöjd (gul), beroende på SANT-bokstavtalet i den 1:a (hor) och 2:a (vert) satsen.

XOR-tillfredsställelse

Lösa ett XOR-SAT-exempel med Gaussisk eliminering

Given formel
("⊕" betyder XOR, den röda satsen är valfri)
( a ⊕ c ⊕ d ) ∧ ( b ⊕¬ c ⊕ d ) ∧ ( a ⊕ b ⊕¬ d ) ∧ ( a ⊕¬ b ⊕¬ c ) ∧ (¬ a ⊕ b ⊕ c )

Ekvationssystem
("1" betyder SANT, "0" betyder FALSK)
Varje sats leder till en ekvation.
	a	⊕		c	⊕		d	= 1
	b	⊕	¬	c	⊕		d	= 1
	a	⊕		b	⊕	¬	d	= 1
	a	⊕	¬	b	⊕	¬	c	= 1
¬	a	⊕		b	⊕		c	≃ 1

Normaliserat ekvationssystem
som använder egenskaperna för booleska ringar (¬ x =1⊕ x , x ⊕ x =0)
a	⊕	c	⊕	d	= 1
b	⊕	c	⊕	d	=0
a	⊕	b	⊕	d	=0
a	⊕	b	⊕	c	= 1
a	⊕	b	⊕	c	≃0
(Om den röda ekvationen finns, motsäger den
den sista svarta, så systemet är olösligt.
Därför används Gauss algoritm
endast för de svarta ekvationerna.)

Associerad koefficientmatris

a	b	c	d		linje

1	0	1	1	1	A
0	1	1	1	0	B
1	1	0	1	0	C
1	1	1	0	1	D

Förvandlas till echelonform

a	b	c	d		drift

1	0	1	1	1	A
1	1	0	1	0	C
1	1	1	0	1	D
0	1	1	1	0	B (bytt)

1	0	1	1	1	A
0	1	1	0	1	E = C⊕A
0	1	0	1	0	F = D⊕A
0	1	1	1	0	B

1	0	1	1	1	A
0	1	1	0	1	E
0	0	1	1	1	G = F⊕E
0	0	0	1	1	H = B⊕E

Övergår till diagonal form

a	b	c	d		drift

1	0	1	0	0	I = A⊕H
0	1	1	0	1	E
0	0	1	0	0	J = G⊕H
0	0	0	1	1	H

1	0	0	0	0	K = I⊕J
0	1	0	0	1	L = E⊕J
0	0	1	0	0	J
0	0	0	1	1	H

Lösning:
Om den röda klausulen finns:	Olösbar
Annan:	a = 0 = FALSK
	b = 1 = SANT
	c = 0 = FALSK
	d = 1 = SANT
Som en konsekvens:
R ( a , c , d ) ∧ R ( b ,¬ c , d ) ∧ R ( a , b ,¬ d ) ∧ R ( a ,¬ b ,¬ c ) ∧ R (¬ a , b , c )
är inte 1-i-3-tillfredsställande,
medan ( a ∨ c ∨ d ) ∧ ( b ∨ ¬ c ∨ d ) ∧ ( a ∨ b ) ∨ ¬ d ) ∧ ( a ∨ ¬ b ∨ ¬ c )
är 3-tillfredsställande med a = c =FALSK och b = d =SANT.

Ett annat specialfall är klassen av problem där varje sats innehåller XOR (dvs. exklusiv eller ) snarare än (vanliga) ELLER-operatorer. Detta är i P , eftersom en XOR-SAT-formel också kan ses som ett system av linjära ekvationer mod 2, och kan lösas i kubiktid genom gaussisk eliminering ; se rutan för ett exempel. Denna omarbetning är baserad på släktskapet mellan booleska algebror och booleska ringar, och det faktum att aritmetisk modulo två bildar ett ändligt fält . Eftersom en XOR b XOR c utvärderas till TRUE om och endast om exakt 1 eller 3 medlemmar av { a , b , c } är TRUE, är varje lösning av 1-i-3-SAT-problemet för en given CNF-formel också en lösning av XOR-3-SAT-problemet, och i sin tur är varje lösning av XOR-3-SAT en lösning av 3-SAT, jfr. bild. Som en konsekvens är det för varje CNF-formel möjligt att lösa XOR-3-SAT-problemet som definieras av formeln, och baserat på resultatet dra slutsatsen att antingen 3-SAT-problemet är lösbart eller att 1-i-3- SAT-problemet är olösligt.

Förutsatt att komplexitetsklasserna P och NP inte är lika , är varken 2-, Horn- eller XOR-tillfredsställelse NP-komplett, till skillnad från SAT.

Schäfers dikotomisats

Restriktionerna ovan (CNF, 2CNF, 3CNF, Horn, XOR-SAT) gjorde att de betraktade formlerna var konjunktioner av underformler; varje begränsning anger en specifik form för alla underformler: till exempel kan endast binära satser vara underformler i 2CNF.

Schaefers dikotomisats säger att för varje begränsning till booleska funktioner som kan användas för att bilda dessa underformler, är motsvarande tillfredsställbarhetsproblem i P eller NP-komplett. Medlemskapet i P av tillfredsställbarheten av formlerna 2CNF, Horn och XOR-SAT är specialfall av detta teorem.

Följande tabell sammanfattar några vanliga varianter av SAT.


Koda	namn	Restriktioner	Krav	Klass
3SAT	3-tillfredsställelse	Varje sats innehåller 3 bokstaver.	Minst en bokstav måste vara sann.	NPC
2SAT	2-tillfredsställelse	Varje sats innehåller 2 bokstaver.	Minst en bokstav måste vara sann.	P
1-i-3-SAT	Exakt-1 3-SAT	Varje sats innehåller 3 bokstaver.	Exakt en bokstav måste vara sann.	NPC
1-i-3-SAT+	Exakt-1 Positiv 3-SAT	Varje sats innehåller 3 positiva bokstaver.	Exakt en bokstav måste vara sann.	NPC
NAE3SAT	Inte-alla-lika 3-tillfredsställelse	Varje sats innehåller 3 bokstaver.	Antingen en eller två bokstaver måste vara sanna.	NPC
NAE3SAT+	Inte alla lika positiva 3-SAT	Varje sats innehåller 3 positiva bokstaver.	Antingen en eller två bokstaver måste vara sanna.	NPC
PL-SAT	Planar SAT	Incidensgrafen (klausulvariabelgraf) är plan .	Minst en bokstav måste vara sann.	NPC
LSAT	Linjär SAT	Varje sats innehåller 3 bokstaver, skär högst en annan sats, och skärningspunkten är exakt en bokstavlig.	Minst en bokstav måste vara sann.	NPC
HORN-LÖR	Horn tillfredsställelse	Hornklausuler (högst en positiv bokstavlig).	Minst en bokstav måste vara sann.	P
XOR-SAT	Xor tillfredsställelse	Varje sats innehåller XOR-operationer snarare än ELLER.	XOR för alla bokstaver måste vara sant.	P

Förlängningar av SAT

En tillägg som har vunnit betydande popularitet sedan 2003 är satisfiability modulo theories ( SMT ) som kan berika CNF-formler med linjära begränsningar, arrayer, alla olika begränsningar, otolkade funktioner etc. Sådana tillägg förblir vanligtvis NP-kompletta, men mycket effektiva lösare är nu tillgänglig som kan hantera många sådana typer av begränsningar.

Tillfredsställbarhetsproblemet blir svårare om både "för alla" ( ∀ ) och "det finns" ( ∃ ) kvantifierare tillåts binda de booleska variablerna. Ett exempel på ett sådant uttryck skulle vara $\forall x \forall y \exists z (x \lor y \lor z) \land (\neg x \lor \neg y \lor \neg z)$ ; den är giltig, eftersom för alla värden på x och y kan ett lämpligt värde på z hittas, dvs. z =SANT om både x och y är FALSK, och z =FALSK annars. SAT själv (tyst) använder endast ∃ kvantifierare. Om endast ∀ kvantifierare tillåts istället erhålls det så kallade tautologiproblemet som är co -NP - komplett . Om båda kvantifierarna är tillåtna kallas problemet för det kvantifierade booleska formelproblemet ( QBF ), som kan visas vara PSPACE-komplett . Det är en allmän uppfattning att PSPACE-kompletta problem är strikt svårare än något problem i NP, även om detta ännu inte har bevisats. Genom att använda mycket parallella P-system kan QBF-SAT-problem lösas i linjär tid.

Vanlig SAT frågar om det finns minst en variabeltilldelning som gör formeln sann. En mängd olika varianter handlar om antalet sådana uppdrag:

MAJ-SAT frågar om majoriteten av alla uppdrag gör formeln SANT. Den är känd för att vara komplett för PP , en sannolikhetsklass.
#SAT , problemet med att räkna hur många variabeltilldelningar som uppfyller en formel, är ett räkneproblem, inte ett beslutsproblem, och är #P-komplett .
UNIK SAT är problemet med att avgöra om en formel har exakt en uppgift. Den är komplett för USA, komplexitetsklassen som beskriver problem som kan lösas av en icke-deterministisk polynomtids- Turing-maskin som accepterar när det finns exakt en icke-deterministisk acceptansväg och förkastar något annat.
UNAMBIGUOUS-SAT är namnet på tillfredsställbarhetsproblemet när inmatningen är begränsad till formler som har högst en tillfredsställande tilldelning. Problemet kallas även USAT . En lösningsalgoritm för UNAMBIGUOUS-SAT tillåts uppvisa vilket beteende som helst, inklusive ändlös looping, på en formel som har flera tillfredsställande uppdrag. Även om detta problem verkar lättare, har Valiant och Vazirani visat att om det finns en praktisk (dvs. randomiserad polynom-tid ) algoritm för att lösa det, så kan alla problem i NP lösas lika enkelt.
MAX-SAT , problemet med maximal tillfredsställelse , är en FNP- generalisering av SAT. Den frågar efter det maximala antalet klausuler som kan uppfyllas av varje uppdrag. Den har effektiva approximationsalgoritmer , men är NP-svår att lösa exakt. Ännu värre, det är APX -komplett, vilket betyder att det inte finns något polynom-tidsapproximationsschema (PTAS) för detta problem om inte P=NP.
WMSAT är problemet med att hitta en tilldelning av minimivikt som uppfyller en monoton boolesk formel (dvs en formel utan någon negation). Vikter av propositionella variabler ges i inmatningen av problemet. Vikten av en uppgift är summan av vikterna av sanna variabler. Det problemet är NP-komplett (se Th. 1 of ).

Andra generaliseringar inkluderar tillfredsställelse för logik av första och andra ordningen , problem med begränsningstillfredsställelse, 0-1 heltalsprogrammering .

Att hitta ett tillfredsställande uppdrag

Även om SAT är ett beslutsproblem , minskar sökproblemet med att hitta ett tillfredsställande uppdrag till SAT . Det vill säga att varje algoritm som svarar korrekt om en instans av SAT är lösbar kan användas för att hitta en tillfredsställande uppgift. Först ställs frågan om den givna formeln Φ. Om svaret är "nej" är formeln otillfredsställande. Annars ställs frågan på den delvis instansierade formeln Φ { x 1 ₌ TRUE} , dvs Φ med den första variabeln x ₁ ersatt av TRUE, och förenklas därefter. Om svaret är "ja", då x ₁ =SANT, annars x ₁ =FALSK. Värden för andra variabler kan hittas i efterhand på samma sätt. Totalt n +1 körningar av algoritmen, där n är antalet distinkta variabler i Φ.

Denna egenskap används i flera satser inom komplexitetsteorin:

NP ⊆ P/poly ⇒ PH = Σ ₂ ( Karp–Lipton-satsen )

NP ⊆ BPP ⇒ NP = RP

P = NP ⇒ FP = FNP

Algoritmer för att lösa SAT

Eftersom SAT-problemet är NP-komplett är endast algoritmer med exponentiell värsta tänkbara komplexitet kända för det. Trots detta utvecklades effektiva och skalbara algoritmer för SAT under 2000-talet och har bidragit till dramatiska framsteg i vår förmåga att automatiskt lösa probleminstanser som involverar tiotusentals variabler och miljontals begränsningar (dvs. klausuler). Exempel på sådana problem inom elektronisk designautomation (EDA) inkluderar formell likvärdighetskontroll , modellkontroll , formell verifiering av pipelined mikroprocessorer , automatisk testmönstergenerering , routing av FPGA , planering och schemaläggningsproblem , och så vidare. En SAT-lösande motor anses också vara en viktig komponent i den elektroniska designautomationsverktygslådan .

Viktiga tekniker som används av moderna SAT-lösare inkluderar Davis–Putnam–Logemann–Loveland-algoritmen (eller DPLL), konfliktdriven klausulinlärning (CDCL) och stokastiska lokala sökalgoritmer som WalkSAT . Nästan alla SAT-lösare inkluderar time-outs, så de kommer att avslutas inom rimlig tid även om de inte kan hitta en lösning. Olika SAT-lösare kommer att tycka att olika instanser är lätta eller svåra, och vissa utmärker sig på att bevisa otillfredsställelse och andra på att hitta lösningar. Nyligen har försök gjorts att lära sig en instanss tillfredsställelse med hjälp av djupinlärningstekniker.

SAT-lösare utvecklas och jämförs i SAT-lösningstävlingar. Moderna SAT-lösare har också betydande inverkan på områdena mjukvaruverifiering, begränsningslösning inom artificiell intelligens och operationsforskning, bland annat.

Se även

Anteckningar

externa länkar

SAT-spel : försök lösa ett booleskt tillfredsställelseproblem själv
Den internationella SAT-tävlingens webbplats
Internationell konferens om teori och tillämpningar av tillfredsställelsetestning
Journal on Satisfiability, Boolean Modeling and Computation
SAT Live, en samlad webbplats för forskning om tillfredsställbarhetsproblemet
Årlig utvärdering av MaxSAT-lösare

Vidare läsning

(efter publiceringsdatum)

Garey, Michael R .; Johnson, David S. (1979). Datorer och svårhanterlighet: En guide till teorin om NP-fullständighet. WH Freeman. s. A9.1: LO1–LO7, s. 259–260. ISBN 0-7167-1045-5 .
Marques-Silva, J.; Glass, T. (1999). "Kombinationell likvärdighetskontroll med hjälp av tillfredsställelse och rekursivt lärande". Design, Automation and Test in Europe Conference and Exhibition, 1999. Proceedings (Cat. No. PR00078) (PDF) . sid. 145. doi : 10.1109/DATE.1999.761110 . ISBN 0-7695-0078-1 . Arkiverad (PDF) från originalet 2022-10-09.
Clarke, E.; Biere, A.; Raimi, R.; Zhu, Y. (2001). "Bounded Model Checking Using Satisfiability Solving". Formella metoder i systemdesign . 19 : 7–34. doi : 10.1023/A:1011276507260 . S2CID 2484208 .
Giunchiglia, E.; Tacchella, A. (2004). Giunchiglia, Enrico; Tacchella, Armando (red.). Teori och tillämpningar av tillfredsställelsetestning . Föreläsningsanteckningar i datavetenskap. Vol. 2919. doi : 10.1007/b95238 . ISBN 978-3-540-20851-8 . S2CID 31129008 .
Babic, D.; Bingham, J.; Hu, AJ (2006). "B-Cubing: Nya möjligheter för effektiv SAT-lösning" ( PDF) . IEEE-transaktioner på datorer . 55 (11): 1315. doi : 10.1109/TC.2006.175 . S2CID 14819050 .
Rodriguez, C.; Villagra, M.; Baran, B. (2007). "Asynkrona lagalgoritmer för Boolean Satisfiability" (PDF) . 2007 2:a bioinspirerade modeller av nätverks-, informations- och datorsystem . s. 66–69. doi : 10.1109/BIMNICS.2007.4610083 . S2CID 15185219 .
Gomes, Carla P. ; Kautz, Henry; Sabharwal, Ashish; Selman, Bart (2008). "Satisfiability Solvers". I Harmelen, Frank Van; Lifschitz, Vladimir; Porter, Bruce (red.). Handbok i kunskapsrepresentation . Grunderna för artificiell intelligens. Vol. 3. Elsevier. s. 89–134. doi : 10.1016/S1574-6526(07)03002-7 . ISBN 978-0-444-52211-5 .
Vizel, Y.; Weissenbacher, G.; Malik, S. (2015). "Booleska tillfredsställelselösare och deras tillämpningar i modellkontroll". IEEE:s förfaranden . 103 (11): 2021–2035. doi : 10.1109/JPROC.2015.2455034 . S2CID 10190144 .
Knuth, Donald E. (2022). "Kapitel 7.2.2.2: Tillfredsställelse". Konsten att programmera datorer . Vol. 4B: Kombinatoriska algoritmer, del 2. Addison-Wesley Professional. s. 185–369. ISBN 978-0-201-03806-4 .

Den här artikeln innehåller material från en kolumn i ACM SIGDAs e-nyhetsbrev av Prof. Karem Sakallah Originaltext finns tillgänglig här