Powerset konstruktion

I teorin om beräknings- och automatteorin är kraftuppsättningskonstruktionen eller delmängdskonstruktionen en standardmetod för att konvertera en icke-deterministisk finit automat (NFA) till en deterministisk finit automat (DFA ) som känner igen samma formella språk . Det är viktigt i teorin eftersom det fastställer att NFA, trots sin extra flexibilitet, inte kan känna igen något språk som inte kan kännas igen av vissa DFA. Det är också viktigt i praktiken för att konvertera enklare att konstruera NFA:er till mer effektivt körbara DFA:er. Men om NFA har n tillstånd kan den resulterande DFA ha upp till 2 ⁿ tillstånd, ett exponentiellt större antal, vilket ibland gör konstruktionen opraktisk för stora NFAs.

Konstruktionen, ibland kallad Rabin–Scott powerset-konstruktion (eller delmängdskonstruktion) för att skilja den från liknande konstruktioner för andra typer av automater, publicerades först av Michael O. Rabin och Dana Scott 1959.

Intuition

För att simulera driften av en DFA på en given ingångssträng måste man hålla reda på ett enda tillstånd när som helst: det tillstånd som automaten kommer att nå efter att ha sett ett prefix för ingången. För att simulera en NFA måste man däremot hålla reda på en uppsättning tillstånd: alla tillstånd som automaten kan nå efter att ha sett samma prefix för inmatningen, enligt de icke-deterministiska val som görs av automaten. Om, efter ett visst prefix av inmatningen, en uppsättning $S$ av tillstånd kan nås, är efter nästa ingångssymbol $x$ uppsättningen av nåbara tillstånd en deterministisk funktion av $S$ och $x$ . Därför spelar uppsättningarna av nåbara NFA-tillstånd samma roll i NFA-simuleringen som enstaka DFA-tillstånd spelar i DFA-simuleringen, och i själva verket kan uppsättningarna av NFA-tillstånd som förekommer i denna simulering omtolkas som tillstånd för en DFA.

Konstruktion

Powerset-konstruktionen gäller mest direkt för en NFA som inte tillåter tillståndstransformationer utan att konsumera ingångssymboler (aka: "ε-moves"). En sådan automat kan definieras som en 5-tuppel $0 (Q, Σ, T, q, F)$ , där $Q$ är mängden tillstånd, $Σ$ är mängden ingångssymboler, $T$ är övergångsfunktionen (mappning av ett tillstånd och en ingångssymbol till en uppsättning tillstånd), $q 0$ är initialtillståndet och $F$ är uppsättningen av accepterande tillstånd. Motsvarande DFA har tillstånd som motsvarar delmängder av $Q.$ Det initiala tillståndet för DFA är $0 {q}$ , (en-element) uppsättningen av initialtillstånd. Övergångsfunktionen för DFA mappar ett tillstånd $S$ (representerar en delmängd av $Q$ ) och en ingångssymbol $x$ till mängden $T (S, x) = \cup{T (q, x) | q \in S}$ , mängden av alla tillstånd som kan nås genom en $x$ -övergång från ett tillstånd i $S$ . En stat $S$ i DFA är en accepterande stat om och endast om minst en medlem av $S$ är en accepterande stat i NFA.

I den enklaste versionen av kraftmängdskonstruktionen är uppsättningen av alla tillstånd av DFA:n kraftmängd Q , uppsättningen $av$ alla möjliga delmängder av $Q.$ Många tillstånd i den resulterande DFA kan dock vara oanvändbara eftersom de kan vara oåtkomliga från det ursprungliga tillståndet. En alternativ version av konstruktionen skapar endast de stater som faktiskt är tillgängliga.

NFA med ε-moves

För en NFA med ε-rörelser (även kallad en ε-NFA), måste konstruktionen modifieras för att hantera dessa genom att beräkna ε- stängningen av tillstånd: uppsättningen av alla tillstånd som kan nås från något givet tillstånd med enbart ε-rörelser. Van Noord känner igen tre möjliga sätt att införliva denna stängningsberäkning i powersetkonstruktionen:

Beräkna ε-stängningen av hela automaten som ett förbearbetningssteg, producera en likvärdig NFA utan ε-rörelser, använd sedan den vanliga kraftuppsättningskonstruktionen. Den här versionen, som också diskuteras av Hopcroft och Ullman, är enkel att implementera, men opraktisk för automater med ett stort antal ε-rörelser, som vanligtvis förekommer i naturliga språkbehandlingsapplikationer .
Beräkna ε-stängningen $\{q'~|~q\to _{\varepsilon }^{*}q'\}$ för varje tillstånd $q$ som beaktas av algoritmen (och cachelagra resultatet) .
Beräkna ε-stängningen ${\displaystyle \{q'~|~\exists q\in Q',q\to _{\varepsilon }^{*}q'\}} av$ varje delmängd av tillstånd $Q'$ som beaktas av algoritmen, och lägg till dess element till $Q'$ .

Flera initiala tillstånd

Om NFA:er är definierade för att tillåta flera initiala tillstånd, är det initiala tillståndet för motsvarande DFA uppsättningen av alla initiala tillstånd för NFA, eller (om NFA också har ε-rörelser) uppsättningen av alla tillstånd som kan nås från initiala tillstånd av ε-rörelser.

Exempel

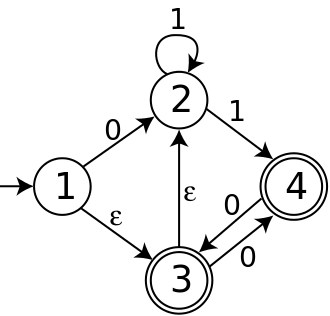
NFA nedan har fyra stater; tillstånd 1 är initialt och tillstånd 3 och 4 accepterar. Dess alfabet består av de två symbolerna 0 och 1, och den har ε-drag.

Det initiala tillståndet för DFA konstruerad från denna NFA är uppsättningen av alla NFA-tillstånd som kan nås från tillstånd 1 genom ε-rörelser; det vill säga det är uppsättningen {1,2,3}. En övergång från {1,2,3} med ingångssymbol 0 måste följa antingen pilen från tillstånd 1 till tillstånd 2, eller pilen från tillstånd 3 till tillstånd 4. Dessutom har varken tillstånd 2 eller tillstånd 4 utgående ε-rörelser. Därför är $T$ ({1,2,3},0) = {2,4}, och av samma resonemang är hela DFA konstruerad från NFA som visas nedan.

Som kan ses i detta exempel finns det fem tillstånd som kan nås från starttillståndet för DFA; de återstående 11 uppsättningarna i kraftuppsättningen för uppsättningen av NFA-stater kan inte nås.

Komplexitet

NFA med 5 stater (vänster) vars DFA (höger) kräver 16 stater.

Eftersom DFA-tillstånden består av uppsättningar av NFA-tillstånd, kan en $n$ -stats NFA konverteras till en DFA med högst $2 n$ tillstånd. För varje $n$ finns det $n$ -tillstånds-NFA så att varje delmängd av tillstånd kan nås från den initiala delmängden, så att den konverterade DFA har exakt 2 $n tillstånd$ , vilket ger Θ( $2n .$ ) värsta tänkbara tidskomplexitet Ett enkelt exempel som kräver nästan så många tillstånd är språket för strängar över alfabetet {0,1} där det finns minst $n$ tecken, varav det $n$ :te från sist är 1. Det kan representeras av en $(n + 1 )$ -tillstånd NFA, men det kräver $2 n$ DFA-tillstånd, ett för varje $n$ -teckensuffix i inmatningen; jfr. bild för $n =4$ .

Ansökningar

Brzozowskis algoritm för DFA-minimering använder powerset-konstruktionen två gånger. Den konverterar ingångs-DFA till en NFA för det omvända språket, genom att vända alla dess pilar och byta roller för initiala och accepterande tillstånd, konverterar NFA tillbaka till en DFA med hjälp av powerset-konstruktionen och upprepar sedan sin process. Dess värsta tänkbara komplexitet är exponentiell, till skillnad från vissa andra kända DFA-minimeringsalgoritmer, men i många exempel fungerar den snabbare än dess värsta tänkbara komplexitet skulle antyda.

Safras konstruktion, som omvandlar en icke-deterministisk Büchi-automat med $n$ tillstånd till en deterministisk Muller-automat eller till en deterministisk Rabin-automat med 2 ^{O( $n$ log $n$ )} -tillstånd, använder kraftuppsättningskonstruktionen som en del av sitt maskineri.

Vidare läsning

Anderson, James Andrew (2006). Automatteori med moderna tillämpningar . Cambridge University Press. s. 43–49. ISBN 978-0-521-84887-9 .