Utöka första sökningen

Utöka första sökningen

Ordning i vilken noderna expanderas
Klass	Sökalgoritm
Datastruktur	Graf
Prestanda i värsta fall	$O(|V|+|E|)=O(b^{d})$
Värsta tänkbara rymdkomplexitet	$O(|V|)=O(b^{d})$

Animerat exempel på en bredd-först-sökning. Svart: utforskad, grå: i kö för att bli utforskad senare

BFS på Maze-lösningsalgoritm

Den övre delen av Tic-tac-toe- spelträdet

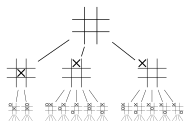
Bredth-first search ( BFS ) är en algoritm för att söka i en träddatastruktur för en nod som uppfyller en given egenskap. Den börjar vid trädroten och utforskar alla noder på nuvarande djup innan den går vidare till noderna på nästa djupnivå. Extra minne, vanligtvis en kö , behövs för att hålla reda på de underordnade noder som påträffades men ännu inte utforskats.

Till exempel, i ett schackslutspel kan en schackmotor bygga spelträdet från den aktuella positionen genom att tillämpa alla möjliga drag, och använda bredd-först-sökning för att hitta en vinstposition för vit. Implicita träd (som viltträd eller andra problemlösande träd) kan vara av oändlig storlek; Bredth-first-sökning kommer garanterat att hitta en lösningsnod om en sådan finns.

Däremot kan (vanlig) djup-först-sökning , som utforskar nodgrenen så långt som möjligt innan man backar och expanderar andra noder, gå vilse i en oändlig gren och aldrig nå lösningsnoden. Iterativ fördjupning av djup-först-sökning undviker den senare nackdelen till priset av att utforska trädets översta delar om och om igen. Å andra sidan kommer båda depth-first-algoritmerna överens utan extra minne.

Bredth-first-sökning kan generaliseras till grafer , när startnoden (ibland hänvisad till som en "söknyckel") uttryckligen ges, och försiktighetsåtgärder vidtas mot att följa en vertex två gånger.

BFS och dess tillämpning för att hitta sammankopplade komponenter i grafer uppfanns 1945 av Konrad Zuse , i hans (avvisade) Ph.D. avhandling om Plankalkül , men detta publicerades inte förrän 1972. Det uppfanns på nytt 1959 av Edward F. Moore , som använde det för att hitta den kortaste vägen ut ur en labyrint, och utvecklades senare av CY Lee till en algoritm för tråddirigering (utgiven 1961).

Pseudokod

Indata : En graf G och en startpunktsrot av G

Utgång : Målstatus. Föräldralänkarna tillbaka till roten

       1  procedur  BFS(  G  ,  root  )  är  2 låt  Q  vara en kö 3 etikett  rot  som utforskat 4  Q  .enqueue(  root  ) 5  medan  Q  inte är tom  gör  6  v  :=  Q  .dequeue() 7  om  v  är målet  då  8  returnera  v  9  för alla  kanter från  v  till  w  i  G  .adjacentEdges(  v  )  gör  10  om  w  inte är märkt som utforskad  sedan  11 etikett  w  as utforskad 12  w  .parent :=  v  13  Q  .enqueue(  w  ) 

Fler detaljer

Denna icke-rekursiva implementering liknar den icke-rekursiva implementeringen av depth-first search , men skiljer sig från den på två sätt:

1. den använder en kö (First In First Out) istället för en stack och
2. den kontrollerar om ett vertex har utforskats innan det ställs i kö för vertexet snarare än att fördröja denna kontroll tills vertexet har tagits ur kö från kön.

Om G är ett träd , kommer att ersätta kön för denna bredd-först-sökalgoritm med en stack en djup-först-sökalgoritm. För allmänna grafer, skulle ersättning av stacken av den iterativa djup-först-sökningsimplementeringen med en kö också producera en bredd-först-sökalgoritm, även om en något icke-standardiserad sådan.

Q - kön innehåller gränsen längs vilken algoritmen för närvarande söker.

Noder kan märkas som utforskade genom att lagra dem i en uppsättning, eller av ett attribut på varje nod, beroende på implementeringen.

Observera att ordet nod vanligtvis är utbytbart med ordet vertex .

Det överordnade attributet för varje nod är användbart för att komma åt noderna i en kortaste väg, till exempel genom att backa från destinationsnoden upp till startnoden, när BFS har körts, och föregångarens noder har ställts in.

Breadth-first-sökning ger ett så kallat Breadth first-träd . Du kan se hur ett brett första träd ser ut i följande exempel.

Exempel

Följande är ett exempel på det breddförsta trädet som erhålls genom att köra en BFS på tyska städer med start från Frankfurt :

En exempelkarta över södra Tyskland med några kopplingar mellan städer

Bredden-första trädet som erhölls när man körde BFS på den givna kartan och startade i Frankfurt

Analys

Komplexitet i tid och rum

Tidskomplexiteten kan uttryckas som ${\displaystyle O(|V|+|E|)} , eftersom varje$ vertex och varje kant kommer att utforskas i värsta fall. $|V|$ är antalet hörn och $|E|$ är antalet kanter i grafen. Observera att $O(|E|)$ kan variera mellan $O(1)$ och $O(|V|^ {2})$ , beroende på hur gles indatagrafen är.

När antalet hörn i grafen är känt i förväg och ytterligare datastrukturer används för att bestämma vilka hörn som redan har lagts till i kön, kan rymdkomplexiteten uttryckas som $O( |V|)$ , där $|V|$ är antalet hörn. Detta är utöver det utrymme som krävs för själva grafen, vilket kan variera beroende på vilken grafrepresentation som används av en implementering av algoritmen.

När man arbetar med grafer som är för stora för att lagra explicit (eller oändliga) är det mer praktiskt att beskriva komplexiteten i bredd-först-sökning i olika termer: att hitta de noder som är på avstånd d från startnoden (mätt i antal av kantövergångar), tar BFS O ( bd ^{. + 1} ) tid och minne, där b är " förgreningsfaktorn " för grafen (den genomsnittliga ut-graden)

Fullständighet

I analysen av algoritmer antas indata till bredd-först-sökning vara en finit graf, representerad som en närliggande lista , närliggande matris eller liknande representation. Vid tillämpningen av graftraversalmetoder i artificiell intelligens kan emellertid inputen vara en implicit representation av en oändlig graf. I detta sammanhang beskrivs en sökmetod som fullständig om den garanterat kan hitta ett måltillstånd om det finns. Bredd-först-sökning är klar, men djup-först-sökning är inte. När den tillämpas på oändliga grafer som representeras implicit, kommer sökningen med bredd-först så småningom att hitta måltillståndet, men första djupsökning kan försvinna i delar av grafen som inte har något måltillstånd och aldrig återvänder.

BFS beställning

En uppräkning av toppen av en graf sägs vara en BFS-ordning om det är den möjliga utmatningen av tillämpningen av BFS på denna graf.

Låt $G=(V,E)$ vara en graf med $n$ hörn. Kom ihåg att $N(v)$ är uppsättningen av grannar till $v$ . Låt $\sigma =(v_{1},\dots ,v_{m})$ vara en lista över distinkta element i $V$ , för $v\in V\setminus \{v_{1},\dots ,v_{m}\}$ , låt $\nu _ {\sigma }(v)$ vara den minsta $i$ så att $v_{i}$ är en granne till $v$ , om en sådan $i$ finns , och vara $\infty$ annars.

Låt $\sigma =(v_{1},\dots ,v_{n})$ vara en uppräkning av hörnen till $V$ . Uppräkningen $\sigma$ sägs vara en BFS-ordning (med källa $v_{1}$ ) om, för alla $1<i\leq n$ , $v_{i}$ är vertex $w\in V\setminus \{v_{1},\dots ,v_{i -1}\}$ så att $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ är minimal. På motsvarande sätt $\sigma$ en BFS-ordning om, för alla $1\leq i<j<k\leq n$ med ${\displaystyle v_{i}\in N(v_{k})\setminus N(v_{j})} , det$ finns en granne $v_{m}$ till $v_{j}$ så att $m<i$ .

Ansökningar

Bredd-först-sökning kan användas för att lösa många problem inom grafteorin, till exempel:

• Kopiera sophämtning , Cheneys algoritm
• Att hitta den kortaste vägen mellan två noder u och v , med väglängden mätt med antalet kanter (en fördel jämfört med djup-först-sökning )
• (Omvänt) Cuthill–McKee mesh-numrering
• Ford–Fulkerson-metod för att beräkna det maximala flödet i ett flödesnätverk
• Serialisering/Deserialisering av ett binärt träd kontra serialisering i sorterad ordning, gör att trädet kan rekonstrueras på ett effektivt sätt.
• Konstruktion av felfunktionen hos Aho-Corasick- mönstermatcharen.
• Testa tvådelad en graf .
• Implementering av parallella algoritmer för att beräkna en grafs transitiva stängning.

Se även

• Djup-första sökning
• Iterativ fördjupning djup-först sökning
• Nivåstruktur
• Lexikografisk bredd-först sökning
• Parallell bredd-först sökning

•   Knuth, Donald E. (1997), The Art of Computer Programming Vol 1. 3:e uppl. , Boston: Addison-Wesley, ISBN 978-0-201-89683-1

externa länkar

• Öppna datastrukturer - Avsnitt 12.3.1 - Bredth-First Search , Pat Morin