Coxeter graf

Coxeter-grafen
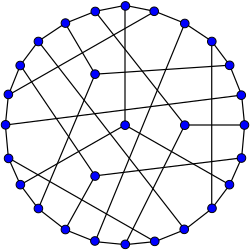Coxeter-grafen
	Coxeter-grafen
Döpt efter	HSM Coxeter
Vertices	28
Kanter	42
Radie	4
Diameter	4
Omkrets	7
Automorfismer	336 ( PGL 2 (7))
Kromatiskt nummer	3
Kromatiskt index	3
Boktjocklek	3
Könummer	2
Egenskaper	; ; ; ; Symmetrisk Avstånd-regelbunden Avstånd-transitiv Cubic Hypohamiltonian
	Tabell över grafer och parametrar

Inom det matematiska området grafteori är Coxeter -grafen en 3- regelbunden graf med 28 hörn och 42 kanter. Det är en av de 13 kända kubikavstånd -reguljära graferna . Den är uppkallad efter Harold Scott MacDonald Coxeter .

Egenskaper

Coxeter-grafen har kromatiskt nummer 3, kromatiskt index 3, radie 4, diameter 4 och omkrets 7. Det är också en graf med 3 vertex och en 3 -kants ansluten graf . Den har boktjocklek 3 och kö nummer 2.

Coxeter-grafen är hypohamiltonisk : den har inte i sig en Hamiltonsk cykel men varje graf som bildas genom att ta bort en enda vertex från den är Hamiltonsk. Den har rätlinjigt korsningsnummer 11 och är den minsta kubiska grafen med det korsningsnumret (sekvens A110507 i OEIS ).

Konstruktion

Den enklaste konstruktionen av en Coxeter-graf är från ett Fano-plan . Ta ⁷ C ₃ = 35 möjliga 3-kombinationer på 7 objekt. Kassera de 7 trillingarna som motsvarar linjerna på Fano-planet och lämna 28 trillingar. Länka två trillingar om de är osammanhängande. Resultatet är Coxeter-grafen. (Se bild .) Denna konstruktion visar Coxeter-grafen som en inducerad subgraf av Kneser-grafen $KG 7,3$ .

Coxeter-grafen kan också konstrueras från den mindre avstånd-reguljära Heawood-grafen genom att konstruera en vertex för varje 6-cykel i Heawood-grafen och en kant för varje disjunkt par av 6-cykler.

Coxeter-grafen kan härledas från Hoffman-Singleton-grafen . Ta valfri vertex v i Hoffman-Singleton-grafen. Det finns en oberoende uppsättning av storlek 15 som inkluderar v . Ta bort de 7 grannarna till v , och hela den oberoende uppsättningen inklusive v , och lämna bakom dig Coxeter-grafen.

Algebraiska egenskaper

Automorfismgruppen i Coxeter-grafen är en grupp av ordning 336. Den verkar transitivt på hörnen, på kanterna och på grafens bågar. Därför är Coxeter-grafen en symmetrisk graf . Den har automorfismer som tar vilken vertex som helst till vilken annan vertex som helst och vilken kant som helst till vilken annan kant som helst. Enligt Foster-folkräkningen är Coxeter-grafen, refererad till som F28A, den enda kubiska symmetriska grafen på 28 hörn.

Coxeter-grafen bestäms också unikt av dess grafspektrum , uppsättningen av grafegenvärden för dess närliggande matris .

Som en finit ansluten vertextransitiv graf som inte innehåller någon Hamiltonsk cykel , är Coxeter-grafen ett motexempel till en variant av Lovász-förmodan , men den kanoniska formuleringen av gissningen kräver en Hamiltonsk väg och verifieras av Coxeter-grafen.

Endast fem exempel på vertextransitiv graf utan Hamiltonska cykler är kända: den fullständiga grafen K _{2 ,} Petersen-grafen , Coxeter-grafen och två grafer härledda från Petersen- och Coxeter-graferna genom att ersätta varje vertex med en triangel.

Det karakteristiska polynomet för Coxeter-grafen är $(x-3)(x-2)^{ 8}(x+1)^{7}(x^{2}+2x-1)^{6}$ . Det är den enda grafen med detta karakteristiska polynom, vilket gör det till en graf som bestäms av dess spektrum.

Galleri

Layouter

Dessa är olika representationer av Coxeter-grafen, med samma vertexetiketter. Det finns fyra färger och sju hörn av varje färg. Varje röd, grön eller blå vertex är ansluten med två hörn av samma färg (tunna kanter som bildar 7-cykler) och till en vit vertex (tjocka kanter).