Bianchi klassificering

I matematik ger Bianchi -klassificeringen en lista över alla verkliga 3-dimensionella Lie-algebror ( upp till isomorfism ). Klassificeringen innehåller 11 klasser, varav 9 innehåller en enda Lie-algebra och två av dem innehåller en familj av Lie-algebra i kontinuumstorlek. (Ibland ingår två av grupperna i de oändliga familjerna, vilket ger 9 istället för 11 klasser.) Klassificeringen är viktig inom geometri och fysik, eftersom de associerade Lie-grupperna fungerar som symmetrigrupper av 3-dimensionella Riemannska grenrör . Den är uppkallad efter Luigi Bianchi , som utarbetade den 1898.

Termen "Bianchi-klassificering" används också för liknande klassificeringar i andra dimensioner och för klassificeringar av komplexa Lie-algebror .

Klassificering i dimension mindre än 3

• ⁰ Dimension 0: Den enda Lie-algebra är den abelska Lie-algebra R .
• Dimension 1: Den enda Lie-algebra är den abelska Lie-algebra R ¹ , med den yttre automorfismgruppen den multiplikativa gruppen av reella tal som inte är noll.
• Dimension 2: Det finns två Lie-algebror:
  • ₍ GL2 ( R ) ¹ ) Den abelska Lie-algebra R2 , med yttre automorfismgrupp .
  • (2) Den lösbara Lie-algebra av 2×2 övre triangulära matriser med spår 0. Den har trivialt centrum och trivial yttre automorfismgrupp. Den associerade enkelt anslutna Lie-gruppen är linjens affina grupp .

Klassificering i dimension 3

Alla 3-dimensionella Lie-algebror andra än typerna VIII och IX kan konstrueras som en halvdirekt produkt av R ² och R , med R som verkar på R ² med en 2 x 2-matris M . De olika typerna motsvarar olika typer av matriser M , som beskrivs nedan.

• Typ I : Detta är den abelska och unimodulära Lie-algebra R ³ . Den enkelt anslutna gruppen har centrum R3 och yttre automorfismgrupp _GL3 ( R ⁾ . Detta är fallet när M är 0.
• Typ II : Heisenberg algebra , som är nilpotent och unimodulär. Den enkelt anslutna gruppen har centrum R och yttre automorfismgrupp GL2 ₍ R ) . Detta är fallet när M är nilpotent men inte 0 (egenvärden alla 0).
• Typ III : Denna algebra är en produkt av R och den 2-dimensionella icke-abelska Lie-algebran. (Det är ett begränsningsfall av typ VI, där ett egenvärde blir noll.) Det är lösbart och inte unimodulärt. Den enkelt sammankopplade gruppen har mitten R och den yttre automorfismgruppen gruppen av reella tal som inte är noll. Matrisen M har ett noll- och ett icke-noll-egenvärde.
• Typ IV : Den algebra som genereras av [ y , z ] = 0, [ x , y ] = y , [ x , z ] = y + z . Det är lösbart och inte unimodulärt. Den enkelt sammankopplade gruppen har trivialcentrum och yttre automorfismgrupp produkten av realerna och en grupp av ordning 2. Matrisen M har två lika stora egenvärden som inte är noll, men är inte diagonaliserbar .
• Typ V : [ y , z ] = 0, [ x , y ] = y , [ x , z ] = z . Lösbar och inte unimodulär. (Ett begränsningsfall av typ VI där båda egenvärdena är lika.) Den enkelt sammankopplade gruppen har trivialt centrum och yttre automorfismgrupp elementen i GL ₂ ( R ) av determinant +1 eller −1. Matrisen M har två lika egenvärden och är diagonaliserbar.
• Typ VI : En oändlig familj: halvdirekta produkter av R ² till R , där matrisen M har distinkta reella egenvärden som inte är noll med summa som inte är noll. Algebrorna är lösbara och inte unimodulära. Den enkelt sammankopplade gruppen har trivialcentrum och yttre automorfismgrupp en produkt av de reella talen som inte är noll och en grupp av ordning 2.
• Typ VI ₀ : Denna Lie-algebra är den halvdirekta produkten av R ² med R , med R där matrisen M har distinkta reella egenvärden som inte är noll med nollsumma. Det är lösbart och unimodulärt. Det är Lie-algebra för den 2-dimensionella Poincaré-gruppen , gruppen av isometrier i det 2-dimensionella Minkowski-utrymmet . Den enkelt sammankopplade gruppen har trivialcentrum och yttre automorfismgrupp produkten av de positiva reella talen med den dihedriska gruppen av ordning 8.
• Typ VII : En oändlig familj: halvdirekta produkter av R ² till R , där matrisen M har icke-reella och icke-imaginära egenvärden. Lösbar och inte unimodulär. Den enkelt sammankopplade gruppen har triviala centrum och yttre automorfismgrupp de realer som inte är noll.
• Typ VII ₀ : Halvdirekt produkt av R ² med R , där matrisen M har imaginära egenvärden som inte är noll. Lösbar och unimodulär. Detta är Lie-algebra för gruppen av isometrier i planet. Den enkelt sammankopplade gruppen har centrum Z och den yttre automorfismgruppen en produkt av de reella talen som inte är noll och en grupp av ordningen 2.
• Typ VIII : Lie-algebra sl ₂ ( R ) av spårlösa 2x2-matriser, associerad med gruppen _SL2 ( R) . Det är enkelt och unimodulärt. Den enkelt sammankopplade gruppen är inte en matrisgrupp; den betecknas med ${\displaystyle {\overline {{\mbox{SL}}(2,\mathbf {R} )}}} ,$ har mitt Z och dess yttre automorfismgrupp har ordning 2.
• Typ IX : Lie-algebra för den ortogonala gruppen O ₃ ( R ). Den betecknas med 𝖘𝖔(3) och är enkel och unimodulär. Den motsvarande enkelt anslutna gruppen är SU(2) ; den har center of order 2 och trivial yttre automorfismgrupp, och är en rotationsgrupp .

Klassificeringen av 3-dimensionella komplexa Lie-algebror är liknande förutom att typerna VIII och IX blir isomorfa, och typerna VI och VII blir båda en del av en enda familj av Lie-algebror.

De anslutna 3-dimensionella Lie-grupperna kan klassificeras enligt följande: de är en kvot av motsvarande enkelt sammankopplade Lie-grupp av en diskret undergrupp av mitten, så de kan avläsas från tabellen ovan.

Grupperna är relaterade till de 8 geometrierna i Thurstons geometriseringsförmodan . Närmare bestämt kan sju av de åtta geometrierna realiseras som ett vänsterinvariant mått på den enkelt sammankopplade gruppen (ibland på mer än ett sätt). Thurstongeometrin av typ S ² × R kan inte realiseras på detta sätt.

Strukturkonstanter

De tredimensionella Bianchi-utrymmena tillåter var och en uppsättning av tre dödande vektorfält $\xi _{i}^{(a)}$ som följer följande egenskap:

$\left({\frac {\partial \xi _{i}^{(c)}}{\partial x^{k}}}-{\frac {\partial \xi _{k}^{(c)}}{\partial x^{i}} }\right)\xi _{(a)}^{i}\xi _{(b)}^{k}=C_{\ ab}^{c}$

där $C_{\ ab}^{c}$ , gruppens "strukturkonstanter", bildar en antisymmetrisk tensor av konstant ordning tre i dess två nedre index. För varje tredimensionellt Bianchi-rum, ges ${\displaystyle C_{\ ab}^{c}} av relationen$

$C_{\ ab}^{c}=\varepsilon _{abd}n^{cd}-\ delta _{a}^{c}a_{b}+\delta _{b}^{c}a_{a}$

där $\varepsilon _{abd}$ är Levi-Civita-symbolen , $\delta _{a}^{c}$ är Kroneckerdeltat och vektorn $a_{a}=(a,0,0)$ och diagonal tensor $n^{cd}$ beskrivs i följande tabell, där $n^{(i)}$ ger det i: te egenvärdet för $n^{cd}$ ; parametern a löper över alla positiva reella tal :

Typ Bianchi	$a$	$n^{(1)}$	$n^{(2)}$	$n^{(3)}$	klass	anteckningar	grafisk (bild 1)
jag	0	0	0	0	A	beskriver det euklidiska rummet	vid ursprunget
II	0	1	0	0	A		intervall [0,1] längs $n^{(1)}$
III	1	0	1	-1	B	underfallet av typ VI a med $a=1$	projicerar till fjärde kvadranten av a = 0-planet
IV	1	0	0	1	B		vertikal öppen yta mellan första och fjärde kvadranten av a = 0-planet
V	1	0	0	0	B	har en hyperpseudosfär som specialfall	intervallet (0,1] längs axeln a
VI0	0	1	-1	0	A		fjärde kvadranten av horisontalplanet
VI a	$a$	0	1	-1	B	när $a=1$ , motsvarande typ III	projicerar till fjärde kvadranten av a = 0-planet
VII0	0	1	1	0	A	har det euklidiska rummet som specialfall	första kvadranten av horisontalplanet
VII a	$a$	0	1	1	B	har en hyperpseudosfär som specialfall	projicerar till första kvadranten av a = 0-planet
VIII	0	1	1	-1	A		sjätte oktant
IX	0	1	1	1	A	har en hypersfär som specialfall	andra oktant

Figur 1. Parameterutrymmet som ett 3-plan (klass A) och ett ortogonalt halvt 3-plan (klass B) i R ⁴ med koordinater ( n ⁽¹⁾ , n ⁽²⁾ , n ^{(3) ,} a ) , visar de kanoniska representanterna för varje Bianchi-typ.

Standard Bianchi-klassificeringen kan härledas från de strukturella konstanterna i följande sex steg:

1. På grund av antisymmetrin $C_{ab}^{c}=-C_{ba}^{c}$ finns det nio oberoende konstanter $C_ {ab}^{c}$ . Dessa kan representeras ekvivalent av de nio komponenterna i en godtycklig konstant Cab : ^,
   
   
   ${\displaystyle C_{ab}^{c}=\varepsilon _{abd}C^{dc},} där$ ε _abd är den totalt antisymmetriska tredimensionella Levi-Civita-symbolen (ε ₁₂₃ = 1). Substitution av detta uttryck för $C_{ab}^{c}$ i Jacobi-identiteten , resulterar i $\varepsilon _{abd} C^{bd}C^{ac}=0.$
2. 
   
   Strukturkonstanterna kan transformeras som: $C^{ab}=\left(\det {A}\right)^{-1}A_{m}^{a}A_{n}^{b}{\acute {C}}^{ mn}.$ Utseendet av det A i denna formel beror på att symbolen ε _abd transformeras som tensordensitet:
   ${\displaystyle \varepsilon _{abc}=\left(\det {A}\right)D_{a}^{m}D_{b}^ {n}D_{c}^{d}{\acute {\varepsilon }}_{mnd}} ,$ där έ _mnd ≡ ε _mnd . Genom denna transformation är det alltid möjligt att reducera matrisen C ^ab till formen:
   $C^{ab}={\begin{bmatrix}n_{1}&0&0\\0&C^{22}&C^{23}\\0&C^{32}&C^{33}\end{bmatrix}} .$ Efter ett sådant val har man fortfarande friheten att göra triadtransformationer men med begränsningarna $A_{2}^{1}=A_{3}^{1}=0$ och $A_{1}^{2}=A_{1}^{3}=0.$
3. 
   Nu ger Jacobi-identiteterna bara en begränsning: $\left(C^{23}-C^{32}\right)n_{1}=0.$
4. Om n ₁ ≠ 0 så är C ²³ – C ³² = 0 och genom de återstående transformationerna med ${\displaystyle A_{\bar {b}}^{ \bar {a}}\neq 0,\quad {\bar {a}},{\bar {b}}={\bar {2}},{\bar {3}}} , 2 × 2-$ matrisen $C^{{\bar {a}}{\bar {b}}}$ i
   
   C ^ab kan göras diagonalt. Då ${\displaystyle C^{ab}={\begin{bmatrix}n_{1}&0&0\\0&n_{2}&0\\0&0&n_{3}\end{bmatrix}}.} Diagonalitetsvillkoret för$ C ab ^bevaras under transformationerna med diagonal $A_{b}^{a}$ . Under dessa transformationer, de tre parametrarna n ₁ , n ₂
   
   , n ₃ ändras på följande sätt: $n_{a}=\left(A_{1}^{1}A_{2}^{2}A_{3}^{3}\right)\left(A_{a}^{a}\ höger)^{2}{\acute {n}}_{a},{\text{ingen summering över}}\ a.$ Genom dessa diagonala transformationer, modulen för valfri n _a (om det inte är noll) kan göras lika med enhet. Med hänsyn till att den samtidiga ändringen av tecken för alla n _a inte ger något nytt, kommer man till följande oföränderligt olika mängder för talen n ₁ , n ₂ , n ₃ (ovariabelt olika i den meningen att det inte finns något sätt att gå från en till en annan genom någon transformation av triaden
   ${\displaystyle e_{a}^{\bar {a}}=A_{\bar {b}}^{\bar {a}}e_{a}^{\bar {b}}} ),$ dvs. följande olika typer av homogena utrymmen med diagonal matris ^Cab : ${\begin{matrix}Bianchi\ IX&:&(n_{1},n_{2},n_{3})&=&(1,1,1),\\Bianchi\ VIII&:&(n_ {1},n_{2},n_{3})&=&(1,1,-1),\\Bianchi\ VII_{0}&:&(n_{1},n_{2},n_{ 3})&=&(1,1,0),\\Bianchi\ VI_{0}&:&(n_{1},n_{2},n_{3})&=&(1,-1, 0),\\Bianchi\ II&:&(n_{1},n_{2},n_{3})&=&(1,0,0).\end{matris}}$
5. ₀₀ Betrakta nu fallet n ₁ = 0. Det kan också hända i det fallet att C ²³ – C ³² = 0. Detta återgår till situationen som redan analyserats i föregående steg men med tilläggsvillkoret n ₁ = 0. Nu, allt väsentligt olika typer för mängderna n ₁ , n ₂ , n ₃ är (0, 1, 1), (0, 1, −1), (0, 0, 1) och (0, 0, 0). De tre första upprepar typerna VII , VI , II
   . Följaktligen uppstår endast en ny typ: $Bianchi\ I\ :\ (n_{1},n_{2},n_{3})\ =\ (0,0,0).$
6. Det enda fallet som finns kvar är n ₁ = 0 och C ²³ – C ³² ≠ 0. Nu är 2 × 2-matrisen ${\displaystyle C^{{\bar { a}}{\bar {b}}}({\bar {a}},{\bar {b}}=2,3)} är icke-symmetrisk och kan inte göras diagonal genom transformationer$ med $A_{\bar {b}}^{\bar {a}}\neq 0$
   
   . Dess symmetriska del kan dock diagonaliseras, det vill säga 3 × 3-matrisen C ^ab kan reduceras till formen: $C^{ab}={\ start{bmatrix}0&0&0\\0&n_{2}&a\\0&-a&n_{3}\end{bmatrix}},$ där a är ett godtyckligt tal. att detta är gjort återstår fortfarande möjligheten att utföra transformationer med diagonal
   $A_{\bar {b}}^{\bar {a}}$ , under vilken kvantiteterna n ₂ , n ₃ och en förändring enligt följande:
   $n_{2}=\left(A_{1}^{1}A_{2}^{2}A_{3}^{3}\right)^{-1}\left(A_{2} ^{2}\höger)^{2}{\acute {n}}_{2},\quad n_{3}=\left(A_{1}^{1}A_{2}^{2}A_ {3}^{3}\right)^{-1}\left(A_{3}^{3}\right)^{2}{\acute {n}}_{3},\quad a=\ left(A_{1}^{1}\right)^{-1}{\acute {a}}.$ Dessa formler visar att för icke-noll n ₂ , n ₃ , a , kombinationen a ² ( n ₂ n ₃ ) ⁻¹ är en invariant storhet. Genom ett val av $A_{1}^{1}$ kan man ställa villkoret a > 0 och efter att detta är gjort, valet av tecknet för $A_{3}^{3}\left(A_{2}^{2}\right)^{-1}$
   tillåter en att ändra båda tecknen för n ₂ och n ₃ samtidigt, det vill säga mängden ( n ₂ , n ₃ ) är ekvivalent med mängden (− n ₂ ,− n ₃ ). Det följer att det finns följande fyra olika möjligheter:
   
   $(a,n_{2},n_{3})=(a,0,0),(a,0,1),(a,1,1),(a,1,-1).$ För de två första kan talet a omvandlas till enhet genom att välja parametrarna $A_{1}^{1}$ och
   $A_{3}^{3}\left(A_{2}^{2}\right)^{-1}$ . För de andra två möjligheterna är båda dessa parametrar redan fixerade och a förblir ett invariant och godtyckligt positivt tal. Historiskt har dessa fyra typer av homogena utrymmen klassificerats som:
   ${\begin{matrix}Bianchi\ V&:&n_{1}=0,\ (a,n_{2},n_{3})&=&(1,0,0),\\Bianchi\ IV& :&n_{1}=0,\ (a,n_{2},n_{3})&=&(1,0,1),\\Bianchi\ VII&:&n_{1}=0,\ (a, n_{2},n_{3})&=&(a,1,1),\\Bianchi\ III&:&n_{1}=0,\ (a,n_{2},n_{3})&= &(1,1,-1),\\Bianchi\ VI&:&n_{1}=0,\ (a,n_{2},n_{3})&=&(a,1,-1).\ end{matrix}}$ Typ III är bara ett särskilt fall av typ VI som motsvarar a = 1. Typerna VII och VI ₀₀ innehåller en oändlighet av oföränderligt olika typer av algebror som motsvarar godtyckligheten hos den kontinuerliga parametern a . Typ VII är ett särskilt fall av VII som motsvarar a = 0 medan typ VI är ett speciellt fall av VI som också motsvarar a = 0.

Krökning av Bianchi-utrymmen

Bianchi-utrymmena har egenskapen att deras Ricci-tensorer kan separeras i en produkt av de basvektorer som är associerade med rummet och en koordinatoberoende tensor.

För ett givet mått :

$ds^{2}=\gamma _{ab}\xi _{i}^{(a)} \xi _{k}^{(b)}dx^{i}dx^{k}$

(där $\xi _{i}^{(a)}dx^{i}$ är 1-former ), Ricci-kurvaturtensorn $R_{ik }$ ges av:

$R_{ik}=R_{(a)(b)}\xi _{i}^{(a)} \xi _{k}^{(b)}$

$R_{(a)(b)}={\frac {1}{2}} \left[C_{\ \ b}^{cd}\left(C_{cda}+C_{dca}\right)+C_{\ cd}^{c}\left(C_{ab}^{\ \ d }+C_{ba}^{\ \ d}\right)-{\frac {1}{2}}C_{b}^{\ cd}C_{acd}\right]$

där indexen på strukturkonstanterna höjs och sänks med $\gamma _{ab}$ vilket inte är en funktion av $x^{i}$ .

Kosmologisk tillämpning

Inom kosmologi används denna klassificering för en homogen rumtid av dimension 3+1. Den 3-dimensionella Lie-gruppen är som symmetrigruppen för den 3-dimensionella rymdliknande skivan, och Lorentz-måttet som uppfyller Einsteins ekvation genereras genom att variera de metriska komponenterna som en funktion av t. Friedmann –Lemaître–Robertson–Walker-måtten är isotropa, vilket är speciella fall av typerna I, V, $\scriptstyle {\text{VII}}_{h}$ och IX. Bianchi typ I-modellerna inkluderar Kasner-måttet som ett specialfall. Bianchi IX-kosmologierna inkluderar Taub-metriken . Emellertid styrs dynamiken nära singulariteten ungefär av en serie på varandra följande Kasner (Bianchi I) perioder. Den komplicerade dynamiken, som i huvudsak motsvarar biljardrörelse i en del av hyperboliskt utrymme, uppvisar ett kaotiskt beteende och heter Mixmaster ; dess analys hänvisas till som BKL-analysen efter Belinskii, Khalatnikov och Lifshitz. Nyare arbete har etablerat en relation mellan (super)gravitationsteorier nära en rymdliknande singularitet (BKL-gräns) med Lorentzian Kac–Moody algebras , Weyl-grupper och hyperboliska Coxeter-grupper . Andra nyare arbeten handlar om Kasner-kartans diskreta karaktär och en kontinuerlig generalisering. I ett utrymme som är både homogent och isotropiskt bestäms metriken helt och hållet, och endast krökningens tecken lämnas fritt. Att endast anta rymdhomogenitet utan ytterligare symmetri såsom isotropi ger betydligt större frihet att välja måttenhet. Följande avser rymddelen av metriken vid en given tidpunkt t med antagande av en synkron ram så att t är samma synkroniserade tid för hela rummet.

Homogenitet innebär identiska metriska egenskaper på alla punkter i rummet. En exakt definition av detta begrepp innebär att man överväger uppsättningar av koordinattransformationer som omvandlar rummet till sig självt, dvs lämnar dess metriska oförändrade: om linjeelementet före transformationen är

$dl^{2}=\gamma _{\alpha \beta }\left(x^{1} ,x^{2},x^{3}\right)dx^{\alpha }dx^{\beta },$

sedan efter transformation är samma linjeelement

$dl^{2}=\gamma _{\alpha \beta }\left( x^{\prime 1},x^{\prime 2},x^{\prime 3}\right)dx^{\prime \alpha }dx^{\prime \beta },$

med samma funktionella beroende av γ _αβ på de nya koordinaterna. (För en mer teoretisk och koordinatoberoende definition av homogent utrymme se homogent utrymme ). Ett rum är homogent om det tillåter en uppsättning transformationer ( en grupp av rörelser ) som för en given punkt till positionen för vilken annan punkt som helst. Eftersom rymden är tredimensionell märks gruppens olika transformationer av tre oberoende parametrar.

Figur 2. Triaden e ^{( a )} ( e ⁽¹⁾ , e ⁽²⁾ , e ⁽³⁾ ) är ett affint koordinatsystem (inklusive som ett specialfall kartesiskt koordinatsystem) vars koordinater är funktioner av de kurvlinjära koordinaterna x _α (x ₁ , x ₂ , x ₃ ).

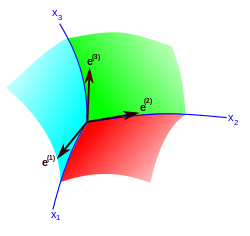
I det euklidiska rummet uttrycks rummets homogenitet genom invariansen av metriken under parallella förskjutningar ( översättningar ) av det kartesiska koordinatsystemet . Varje translation bestäms av tre parametrar - komponenterna i förskjutningsvektorn för koordinatursprunget. Alla dessa transformationer lämnar oföränderliga de tre oberoende differentialerna ( dx , dy , dz ) från vilken linjeelementet är konstruerat. I det allmänna fallet med ett icke-euklidiskt homogent utrymme, lämnar transformationerna av dess grupp av rörelser återigen oföränderliga tre oberoende linjära differentialformer , som dock inte reduceras till totala skillnader för några koordinatfunktioner. Dessa former skrivs som $e_{\alpha }^{(a)}dx^{\alpha }$ där det latinska indexet ( a ) betecknar tre oberoende vektorer (koordinatfunktioner); dessa vektorer kallas a ramfält eller triad. De grekiska bokstäverna märker de tre rymdliknande krökta koordinaterna . En rumslig metrisk invariant konstrueras under den givna gruppen av rörelser med användning av ovanstående former:

$dl^{2}=\eta _{ab}\left(e_{\alpha } ^{(a)}dx^{\alpha }\right)\left(e_{\beta }^{(b)}dx^{\beta }\right)$

 

 

 

 

()

dvs den metriska tensorn är

$\gamma _{\alpha \beta }=\eta _{ab}e_{\alpha }^{(a)}e_{\ beta }^{(b)}$

 

 

 

 

()

där koefficienterna η _ab , som är symmetriska i indexen a och b , är funktioner av tiden. Valet av basvektorer dikteras av rymdens symmetriegenskaper och i allmänhet är dessa basvektorer inte ortogonala (så att matrisen η _ab inte är diagonal).

Den reciproka trippeln av vektorer $e_{(a)}^{\alpha }$ introduceras med hjälp av Kronecker delta

$e_{(a)}^{\alpha }e_{\alpha }^{(b)}=\delta _{a}^{b} ;\quad e_{(a)}^{\alpha }e_{\beta }^{(a)}=\delta _{\alpha }^{\beta }$

 

 

 

 

()

I det tredimensionella fallet kan relationen mellan de två vektortrippelna skrivas explicit

$\mathbf {e} _{(1)}={\frac {1}{v}}\mathbf {e} ^{(2)}\times \mathbf {e} ^{(3)}, \quad \mathbf {e} _{(2)}={\frac {1}{v}}\mathbf {e} ^{(3)}\times \mathbf {e} ^{(1)},\ quad \mathbf {e} _{(3)}={\frac {1}{v}}\mathbf {e} ^{(1)}\times \mathbf {e} ^{(2)},$

 

 

 

 

()

där volymen v är

$v=\left\vert e_{\alpha }^{(a)}\right\vert =\mathbf {e} ^{(1 )}\cdot \mathbf {e} ^{(2)}\times \mathbf {e} ^{(3)},$

med e _{( a )} och e ^{( a )} betraktade som kartesiska vektorer med komponenterna $e_{(a)}^{\alpha }$ och $e_{\alpha } ^{(a)}$ , respektive. Determinanten för den metriska tensorekv . 6b är γ = η v ² där η är determinanten för matrisen η _ab .

De nödvändiga förutsättningarna för utrymmets homogenitet är

$\left({\frac {\partial e_{\alpha }^{(c)}}{\partial x^{\beta }}}-{\frac {\partial e_{\beta }^{( c)}}{\partial x^{\alpha }}}\right)e_{(a)}^{\alpha }e_{(b)}^{\beta }=C_{ab}^{c}.$

 

 

 

 

()

Konstanterna $C_{ab}^{c}$ kallas gruppens strukturkonstanter .

Bevis på ekv. 6e

Invariansen för differentialformerna $e_{\alpha }^{(a)}dx^{\alpha }$ betyder att $e_{\alpha }^{(a)}(x)dx^{\alpha }=e_ {\alpha }^{(a)}(x^{\prime })dx^{\prime \alpha }$ där $e_{\alpha }^{(a)}$ på de två sidorna av ekvationen är samma funktioner för de gamla respektive nya koordinaterna. Multiplicera denna ekvation med ${\displaystyle e_{(a)}^{\beta }(x^{\prime })} ,$ inställning ${\displaystyle dx^{\prime \beta }={\frac {\partial x^{\prime \beta }}{\partial x^{\alpha }}}dx^{\alpha },} och jämföra koefficienter$ för samma skillnader dx α , finner man ${\frac {\partial x^{\prime \beta }}{\partial x^{\alpha }}}=e_{(a)}^{\beta }(x^{\prime })e_ {\alpha }^{(a)}(x).$ Dessa ekvationer är ett system av differentialekvationer som bestämmer funktionerna $x^{\prime \beta }(x)$ för en given bildruta. För att vara integrerbara måste dessa ekvationer uppfylla samma villkor ${\frac {\partial ^{2}x^{\prime \beta }}{\partial x^{\alpha }\partial x^{\gamma }}}={\frac {\partial ^{ 2}x^{\prime \beta }}{\partial x^{\gamma }\partial x^{\alpha }}}.$ Att beräkna derivatorna, finner man $\left[{\frac {\partial e_{(a)}^{\beta }(x^{\prime })}{\partial x^{\prime \delta }}}e_{(b) }^{\delta }(x^{\prime })-{\frac {\partial e_{(b)}^{\beta }(x^{\prime })}{\partial x^{\prime \ delta }}}e_{(a)}^{\delta }(x^{\prime })\right]e_{\gamma }^{(b)}(x)e_{\alpha }^{(a) }(x)=e_{(a)}^{\beta }(x^{\prime })\left[{\frac {\partial e_{\gamma }^{(a)}(x)}{\ partiell x^{\alpha }}}-{\frac {\partial e_{\alpha }^{(a)}(x)}{\partial x^{\gamma }}}\right].$ Multiplicera båda sidor av ekvationerna med ${\displaystyle e_{(d)}^{\alpha }(x)e_ {(c)}^{\gamma }(x)e_{\beta }^{(f)}(x^{\prime })} och skifta differentieringen från$ en faktor till en annan genom att använda ekv. 6c , man får för vänster sida: $e_{\beta }^{(f)}(x^{\prime })\left[{\frac {\partial e_{(d)}^{\beta }(x^{\prime }) }{\partial x^{\prime \delta }}}e_{(c)}^{\delta }(x^{\prime})-{\frac {\partial e_{(c)}^{\beta }(x^{\prime })}{\partial x^{\prime \delta }}}e_{(d)}^{\delta }(x^{\prime })\right]=e_{(c )}^{\beta }(x^{\prime })e_{(d)}^{\delta }(x^{\prime })\left[{\frac {\partial e_{\beta }^{ (f)}(x^{\prime })}{\partial x^{\prime \delta }}}-{\frac {\partial e_{\delta }^{(f)}(x^{\prime })}{\partial x^{\prime \beta }}}\right].$ och för höger, samma uttryck i variabeln x . Eftersom x och x' är godtyckliga måste dessa uttryck reduceras till konstanter för att erhålla ekv. 6e .

Multiplicera med $e_{(c)}^{\gamma }$ , ekv. 6e kan skrivas om i formen

$e_{(a)}^{\alpha }{\frac {\partial e_{(b)}^{\gamma }}{\partial x^{\alpha }}}-e_{(b)} ^{\beta }{\frac {\partial e_{(a)}^{\gamma }}{\partial x^{\beta }}}=C_{ab}^{c}e_{(c)}^ {\gamma }.$

 

 

 

 

()

Ekvation 6e kan skrivas i vektorform som

$\mathbf {e} _{(a)}\times \mathbf {e} _{(b)}{\ text{curl }}\mathbf {e} ^{(c)}=-C_{ab}^{c},$

där återigen vektoroperationerna görs som om koordinaterna x ^α vore kartesiska. Använder ekv. 6d , erhåller man

${\frac {1}{v}}\left(\mathbf {e} ^{(1)}{\text{curl }}\mathbf {e} ^{(1)}\right)= C_{32}^{1},\quad {\frac {1}{v}}\left(\mathbf {e} ^{(2)}{\text{curl }}\mathbf {e} ^{( 1)}\right)=C_{13}^{1},\quad {\frac {1}{v}}\left(\mathbf {e} ^{(3)}{\text{curl }}\ mathbf {e} ^{(1)}\right)=C_{21}^{1}$

 

 

 

 

()

och ytterligare sex ekvationer erhållna genom en cyklisk permutation av index 1, 2, 3.

Strukturkonstanterna är antisymmetriska i sina lägre index sett från deras definition ekv. 6e : $C_{ab}^{c}=-C_{ba}^{c}$ . Ett annat villkor på strukturkonstanterna kan erhållas genom att notera att ekv. 6f kan skrivas i form av kommuteringsrelationer

$\left[X_{a},X_{b}\right]\equiv X_{a}X_{ b}-X_{b}X_{a}=C_{ab}^{c}X_{c}$

 

 

 

 

()

för linjära differentialoperatorer

$X_{a}=e_{(a)}^{\alpha }{\frac {\partial }{\partial x^{\alpha }}}$

 

 

 

 

()

I den matematiska teorin om kontinuerliga grupper ( Lie-grupper ) är operatorerna X _en tillfredsställande villkor ekv. 6h kallas gruppens generatorer . Teorin för Lie-grupper använder operatorer definierade med dödandevektorerna ξ $_{(a)}^{\alpha }}$$e_{(a) }^{\alpha }$ istället för triader . Eftersom i den synkrona metriska ingen av γ _αβ komponenter beror på tid, dödande vektorer (triader) är tidsliknande.

Villkoren motsv . 6h följer av Jacobi-identiteten

$\displaystyle$

och har formen

$C_{ab}^{e}C_{ec}^{d}+C_{bc }^{e}C_{ea}^{d}+C_{ca}^{e}C_{eb}^{d}=0$

 

 

 

 

()

Det är en klar fördel att istället för treindexkonstanterna ${\displaystyle C_{ab}^{c}} använda$ en uppsättning tvåindexstorheter, erhållna genom den dubbla transformationen

$C_{ab}^{c}=e_{abd}C^{dc}$

 

 

 

 

()

där e _abc = e ^abc är enhetens antisymmetriska symbol (med e ₁₂₃ = +1). Med dessa konstanter kommer kommuteringsförhållandena ekv. 6h skrivs som

$e^{abc}X_{b}X_{c}=C^{ad}X_{d}$

 

 

 

 

()

Antisymmetriegenskapen beaktas redan i definitionen ekv. 6k , medan egenskap ekv. 6j tar formen

$e_{bcd}C^{cd}C^{ba}=0$

 

 

 

 

()

Valet av de tre ramvektorerna i differentialformerna $e_{\alpha }^{(a)}dx^{\alpha }$ (och med dem operatorerna X _a ) är inte unik. De kan utsättas för vilken linjär transformation som helst med konstanta koefficienter:

$\mathbf {e} _{(a)}=A_{a}^{b}\mathbf {e} _{(b)}.$

 

 

 

 

()

Storheterna η _ab och Cab beter sig som tensorer (är invarianta ⁾ med avseende på sådana transformationer.

Villkoren motsv . 6m är de enda som strukturkonstanterna måste uppfylla. Men bland de konstanter som är tillåtna av dessa villkor finns det ekvivalenta mängder, i den meningen att deras skillnad är relaterad till en transformation av typen ekv. 6n . Frågan om klassificeringen av homogena utrymmen reduceras till att bestämma alla icke-ekvivalenta uppsättningar av strukturkonstanter. Detta kan göras genom att använda "tensor"-egenskaperna för kvantiteterna Cab ^. , genom följande enkla metod (CG Behr, 1962)

Den asymmetriska tensorn C ^ab kan lösas upp i en symmetrisk och en antisymmetrisk del. Den första betecknas med n ^ab , och den andra uttrycks i termer av dess dubbla vektor a _c :

$C^{ab}=n^{ab}+e^{abc}a_{c}.$

 

 

 

 

()

Substitution av detta uttryck i ekv. 6m leder till tillståndet

$n^{ab}a_{b}=0.$

 

 

 

 

()

Med hjälp av omvandlingarna ekv. 6n den symmetriska tensorn n ^ab bringas till diagonal form med egenvärden n ₁ , n ₂ , n ₃ . Ekvation 6p visar att vektorn a _b (om den finns) ligger längs en av huvudriktningarna för tensorn n ^ab , den som motsvarar egenvärdet noll. Utan förlust av generalitet kan man därför sätta a _b = ( a , 0, 0). Sedan ekv. 6p reduceras till en ₁ = 0, dvs en av storheterna a eller n ₁ måste vara noll. Jacobi-identiteterna tar formen:

$[X_{1},X_{2}]=-aX_{2}+n_{3}X_{3},\quad [X_{2},X_{3}]=n_{1}X_{ 1},\quad [X_{3},X_{1}]=n_{2}X_{2}+aX_{3}.$

 

 

 

 

()

De enda återstående friheterna är teckenändringar av operatorerna X _a och deras multiplikation med godtyckliga konstanter. Detta tillåter att samtidigt ändra tecknet för alla n _a och även att göra kvantiteten positiv (om den skiljer sig från noll). Alla strukturkonstanter kan också göras lika med ±1, om åtminstone en av storheterna a , n ₂ , n ₃ försvinner. Men om alla tre av dessa storheter skiljer sig från noll, lämnar skaltransformationerna förhållandet h = invariant a ² ( n ₂ n ₃ ) ⁻¹ .

Sålunda kommer man fram till Bianchi-klassificeringen som listar de möjliga typerna av homogena utrymmen klassificerade med värdena av a , n ₁ , n ₂ , n ₃ som presenteras grafiskt i fig. 3. I fallet med klass A ( a = 0), typ IX ( n ⁽¹⁾ =1, n ⁽²⁾ =1, n ⁽³⁾ =1) representeras av oktant 2, typ VIII ( n ⁽¹⁾ =1, n ⁽²⁾ =1, n ⁽³⁾ =–1) representeras av oktant 6, medan typ VII ₀ ( n ⁽¹⁾ =1, n ⁽²⁾ =1, n ⁽³⁾ =0) representeras av den första kvadranten av horisontalplanet och typ VI ₀ ( n ⁽¹⁾ =1, n ⁽²⁾ =–1, n ⁽³⁾ =0) representeras av den fjärde kvadranten av detta plan; typ II (( n ⁽¹⁾ =1, n ⁽²⁾ =0, n ⁽³⁾ =0) representeras av intervallet [0,1] längs n ⁽¹⁾ och typ I ( n ⁽¹⁾ =0, n ⁽²⁾ =0, n ⁽³⁾ =0) är i origo. På liknande sätt i klass B-fallet (med n ⁽³⁾ = 0), skjuter Bianchi typ VI _h ( a = h , n ⁽¹⁾ =1, n ⁽²⁾ =–1) ut till den fjärde kvadranten av horisontalplanet och typ VII _h ( a = h , n ⁽¹⁾ =1, n ⁽²⁾ =1) skjuter ut mot den första kvadranten av horisontalplanet; dessa två sista typer är en enkel isomorfismklass som motsvarar en konstantvärdesyta av funktionen h = a ² ( n ⁽¹⁾ n ⁽²⁾ ) ⁻¹ . En typisk sådan yta illustreras i en oktant, vinkeln θ ges av tan θ = | h /2| ^1/2 ; de i de återstående oktanterna erhålls genom rotation genom multiplar av π /2, h alternerande i tecken för en given magnitud | h |. Typ III är en subtyp av VI _h med a =1. Typ V ( a =1, n ⁽¹⁾ =0, n ⁽²⁾ =0) är intervallet (0,1] längs axeln a och typ IV ( a =1, n ⁽¹⁾ =1, n ^{( 2)} =0) är den vertikala öppna ytan mellan den första och fjärde kvadranten av a = 0-planet, där den senare ger klass A-gränsen för varje typ.

Einsteinsekvationerna för ett universum med ett homogent utrymme kan reduceras till ett system av vanliga differentialekvationer som endast innehåller funktioner av tiden med hjälp av ett ramfält. För att göra detta måste man lösa de rumsliga komponenterna av fyra-vektorer och fyra-tensorer längs triaden av basvektorer i rymden:

$R_{(a)(b)}=R_{\alpha \beta }e_{(a)}^{\alpha }e_{(b)}^{\beta },\quad R_{0(a )}=R_{0\alpha }e_{(a)}^{\alpha },\quad u^{(a)}=u^{\alpha }e_{\alpha }^{(a)},$

där alla dessa kvantiteter nu är funktioner av t enbart; de skalära storheterna, energitätheten ε och materiens tryck p , är också funktioner av tiden.

Einsteins ekvationer i vakuum i synkron referensram är

$R_{0}^{0}=-{\frac {1}{2}}{\frac {\ partiell \varkappa _{\alpha }^{\alpha }}{\partial t}}-{\frac {1}{4}}\varkappa _{\alpha }^{\beta }\varkappa _{\beta } ^{\alpha }=0,$

 

 

 

 

()

$R_{\alpha }^{\beta }=-{\frac {1}{2{\ sqrt {-g}}}}{\frac {\partial }{\partial t}}\left({\sqrt {-g}}\varkappa _{\alpha }^{\beta}\right)-P_{ \alpha }^{\beta }=0,$

 

 

 

 

()

$R_{\alpha }^{0}={\frac {1}{2}}\left(\varkappa _{ \alpha ;\beta }^{\beta }-\varkappa _{\beta ;\alpha }^{\beta}\right)=0,$

 

 

 

 

()

där $\varkappa _{\alpha }^{\beta }$ är den 3-dimensionella tensorn ${\displaystyle \varkappa _{\alpha }^{\beta }={\frac {\partial \gamma _{\alpha }^{\beta }}{\partial t}}} ,$ och P _αβ är den 3-dimensionella Ricci-tensorn , som uttrycks av den 3-dimensionella metriska tensorn γ _αβ på samma sätt som R _ik uttrycks med g _ik ; P _αβ innehåller endast rymden (men inte tiden) derivator av γ _αβ . Med hjälp av triader, för ekv. 11 man har helt enkelt

$\varkappa _{(a)(b)}={\frac {\partial \eta _{ab}}{\partial t}},\quad \varkappa _{(a)}^{(b) }={\frac {\partial \eta _{ac}}{\partial t}}\eta ^{cb}.$

Komponenterna i P _{( a ) ( b )} kan uttryckas i termer av kvantiteterna η _ab och strukturkonstanter för gruppen genom att använda tetradrepresentationen av Ricci-tensorn i termer av kvantiteter $\lambda _{abc}=\left(e_{(a)i,k}-e_{(a)k,i}\right)e_{(b)}^{i}e_{ (c)}^{k}$

$R_{(a)(b)}=-{\frac {1}{2}}\left(\lambda _{ab,c}^{c}+\lambda _{ba,c}^{ c}+\lambda _{ca,b}^{c}+\lambda _{cb,a}^{c}+\lambda _{b}^{cd}\lambda _{cda}+\lambda _{ b}^{cd}\lambda _{dca}-{\frac {1}{2}}\lambda _{b}^{cd}\lambda _{acd}+\lambda _{cd}^{c} \lambda _{ab}^{d}+\lambda _{cd}^{c}\lambda _{ba}^{d}\right).$

Efter att ha ersatt treindexsymbolerna $\lambda _{bc}^{a}=C_{bc}^{a}$ med tvåindexsymboler C ^ab och transformationerna:

$\eta _{ad}\eta _{bc}\eta _{cf}e^{def}=\eta e_{abc},\quad e_{abf}e^{cdf}=\delta _{ a}^{c}\delta _{b}^{d}-\delta _{a}^{d}\delta _{b}^{c}$

man får den "homogena" Ricci-tensorn uttryckt i strukturkonstanter:

$P_{(a)}^{(b)}={\frac {1}{2\eta }}\left\{2C^{bd}C_{ad}+C^{db}C_{ad }+C^{bd}C_{da}-C_{d}^{d}\left(C_{a}^{b}+C_{a}^{b}\right)+\delta _{a} ^{b}\left[\left(C_{d}^{d}\right)^{2}-2C^{df}C_{df}\right]\right\}.$

Här höjs och sänks alla index med den lokala metriska tensorn η _ab

$C_{a}^{b}=\eta _{ac}C^{cb},\quad C_{ab}=\eta _{ac}\eta _{bd}C^{cd}.$

Bianchi -identiteterna för den tredimensionella tensorn P _αβ i det homogena utrymmet tar formen

$P_{b}^{c}C_{ca}^{b}+P_{a}^{c}C_{cb} ^{b}=0.$

Med hänsyn till transformationerna av kovarianta derivator för godtyckliga fyrvektorer A _i och fyrtensorer A _ik

$A_{i;k}e_{(a)}^{i}e_{ (b)}^{k}=A_{(a)(b)}-A^{(d)}\gamma _{dab},$

$A_{ik;l }e_{(a)}^{i}e_{(b)}^{k}e_{(c)}^{l}=A_{(a)(b)(c)}-A_{(b) }^{(d)}\gamma _{dac}+A_{(a)}^{(d)}\gamma _{dbc},$

de slutliga uttrycken för triadkomponenterna i Ricci fyrtensor är:

$R_{0}^{0}=-{\frac { 1}{2}}{\frac {\partial \varkappa _{(a)}^{(a)}}{\partial t}}-{\frac {1}{4}}\varkappa _{(a )}^{(b)}\varkappa _{(b)}^{(a)},$

 

 

 

 

()

$R_{(a)}^{(b)}= -{\frac {1}{2{\sqrt {\eta }}}}{\frac {\partial }{\partial t}}\left({\sqrt {\eta }}\varkappa _{(a) }^{(b)}\höger)-P_{(a)}^{(b)},$

 

 

 

 

()

$R_{(a)}^{0}=-{\frac {1}{2}}\varkappa _{(b)}^{(c)}\left(C_{ca}^{b} -\delta _{a}^{b}C_{dc}^{d}\höger).$

 

 

 

 

()

När man sätter upp Einsteinsekvationerna finns det alltså inget behov av att använda explicita uttryck för basvektorerna som funktioner av koordinaterna.

Se även

• Tabell över Lie-grupper
• Lista över enkla Lie-grupper
• BKL singularitet

Bibliografi

• Belinsky, Vladimir A. ; Khalatnikov, IM ; Lifshitz, EM (1971). "Det oscillerande sättet att närma sig en singularitet i homogena kosmologiska modeller med roterande axlar". JETP . 60 (6): 1969–1979.
• Belinsky, Vladimir A. ; Khalatnikov, IM ; Lifshitz, EM (1972). "Konstruktion av en allmän kosmologisk lösning av Einstein-ekvationen med en tidssingularitet". JETP . 62 (5): 1606–1613.
• L. Bianchi, Sugli spazi a tre dimensioni che ammettono un gruppo continuo di movimenti. (På utrymmen av tre dimensioner som tillåter en kontinuerlig grupp av rörelser.) Soc. Ital. Sci. Mem. di Mat. 11, 267 (1898) Engelsk översättning Arkiverad 2020-02-18 på Wayback Machine
•    Cornish, NJ; Levin, JJ (1997a). "The Mixmaster Universe är otvetydigt kaotiskt". I Piran, Tsvi; Ruffini, Remo (red.). Om den senaste utvecklingen av teoretisk och experimentell allmän relativitet, gravitation och relativistiska fältteorier . Uppdrag från åtta Marcel Grossman-mötet. Hebreiska universitetet i Jerusalem: World Scientific. s. 616–618. ISBN 978-9810237936 . OL 13168102M .
•    Cornish, Neil J.; Levin, Janna J. (1997b). "Mixmaster-universumet är kaotiskt". Fysiska granskningsbrev . 78 (6): 998–1001. arXiv : gr-qc/9605029 . Bibcode : 1997PhRvL..78..998C . doi : 10.1103/physrevlett.78.998 . ISSN 0031-9007 . S2CID 119476182 .
•    Cornish, Neil J.; Levin, Janna J. (1997c). "Mixmaster universum: En kaotisk Farey tale". Fysisk granskning D . American Physical Society (APS). 55 (12): 7489–7510. arXiv : gr-qc/9612066 . Bibcode : 1997PhRvD..55.7489C . doi : 10.1103/physrevd.55.7489 . ISSN 0556-2821 . S2CID 17085583 .
•   Ferrando, JJ; Saez, JA (2020). "Homogena tredimensionella Riemannska utrymmen". Klassisk och kvantgravitation . 37 (18): 185011. arXiv : 2004.01877 . Bibcode : 2020CQGra..37r5011F . doi : 10.1088/1361-6382/ab9880 . S2CID 214802205 .
• Guido Fubini Sugli spazi a quattro dimensioni che ammettono un gruppo continuo di movimenti , (Om utrymmen av fyra dimensioner som tillåter en kontinuerlig grupp av rörelser.) Ann. Matta. pura appli. (3) 9, 33-90 (1904); omtryckt i Opere Scelte , a cura dell'Unione matematica italiana e col contributo del Consiglio nazionale delle ricerche, Roma Edizioni Cremonese, 1957–62
•   MacCallum, On the classification of the real four-dimensional Lie algebras , i "On Einstein's path: essays in honor of Engelbert Schucking" redigerad av AL Harvey, Springer ISBN 0-387-98564-6
•    Henneaux, Marc ; Persson, Daniel; Spindel, Philippe (2008). "Rymdliknande singulariteter och dolda gravitationssymmetrier" . Levande recensioner i relativitetsteori . 11 (1): 1. arXiv : 0710.1818 . Bibcode : 2008LRR....11....1H . doi : 10.12942/lrr-2008-1 . PMC 5255974 . PMID 28179821 .
•    Henneaux, Marc ; Persson, Daniel; Wesley, Daniel (2008). "Coxeter-gruppstruktur av kosmologisk biljard på kompakta rumsliga grenrör". Journal of High Energy Physics . 2008 (9): 052. arXiv : 0805.3793 . Bibcode : 2008JHEP...09..052H . doi : 10.1088/1126-6708/2008/09/052 . ISSN 1029-8479 . S2CID 14135098 .
•    Henneaux, Marc (2009). "Kac-Moody algebras och strukturen av kosmologiska singulariteter: ett nytt ljus på Belinskii-Khalatnikov-Lifshitz-analysen". Quantum Mechanics of Fundamental Systems: The Quest for Beauty and Simplicity : 1–11. arXiv : 0806.4670 . doi : 10.1007/978-0-387-87499-9_11 . ISBN 978-0-387-87498-2 . S2CID 18809715 .
• Robert T. Jantzen, Bianchi klassificering av 3-geometrier: originalhandlingar i översättning
• Jantzen, Robert T. (2001). "Spatialt homogen dynamik: en enhetlig bild". Proc. Int. SCH. Phys. "E. Fermi" kurs . LXXXVI . arXiv : gr-qc/0102035 .
•   Landau, Lev D .; Lifshitz, Evgeny M. (1988). Classical Theory of Fields (7:e upplagan). Moskva: Nauka . ISBN 978-5-02-014420-0 . Vol. 2 i kursen teoretisk fysik
• Lifshitz, Evgeny M. ; Khalatnikov, Isaak M. (1963). "Проблемы релятивистской космологии" . Uspekhi Fizicheskikh Nauk . 80 (7): 391–438. doi : 10.3367/UFNr.0080.196307d.0391 . ; Engelsk översättning i Lifshitz, EM; Khalatnikov, IM (1963). "Problem i den relativistiska kosmologin". Framsteg inom fysik . 12 (46): 185. Bibcode : 1963AdPhy..12..185L . doi : 10.1080/00018736300101283 .
•   Ryan, Michael P.; Shepley, Lawrence C. (1975). Homogena relativistiska kosmologier . Princeton-serien i fysik. Princeton, New Jersey: Princeton University Press. ISBN 9780691645209 .
•   Stephani, Hans; Kramer, Dietrich; MacCallum, Malcolm; Hoenselaers, Cornelius; Herlt, Eduard (2003). Exakta lösningar av Einsteins fältekvationer (andra upplagan). Cambridge University Press. ISBN 978-0-521-46136-8 .
•   Wald, Robert M. (1984). Allmän relativitet . Chicago: University of Chicago Press. ISBN 0-226-87033-2 .