3-4-6-12 plattsättning

3-4-6-12 plattsättning

Typ	2-enhetlig plattsättning
Vertex-konfiguration	3.4.6.4 och 4.6.12
Symmetri	p6m, [6,3], (*632)
Rotationssymmetri	p6, [6,3] ⁺ , (632)
Egenskaper	2-uniform, 4- isohedral , 4- isotoxal

I geometrin av det euklidiska planet är 3-4-6-12 plattsättningen en av 20 2-likformiga plattsättningar av det euklidiska planet med regelbundna polygoner , som innehåller regelbundna trianglar , kvadrater , hexagoner och tvåsidiga sidor , ordnade i två vertexkonfigurationer : 3.4. 6.4 och 4.6.12.

Den har hexagonal symmetri , p6m, [6,3], (*632). Det kallas också för en halvregelbunden plattsättning av vissa författare.

Geometri

Dess två vertexkonfigurationer delas med två 1-uniforma plattsättningar:

rhombitrihexagonal plattsättning	stympad trihexagonal plattsättning
3.4.6.4	4.6.12

Det kan ses som en typ av förminskad rhombitrihexagonal plattsättning , med dodecagons som ersätter periodiska uppsättningar av hexagoner och omgivande kvadrater och trianglar. Detta liknar Johnson solid , en förminskad rhombicosidodecahedron , som är en rhombicosidodecahedron med ansikten borttagna, vilket leder till nya dekagonala ansikten. Dual av denna variant visas till höger (deltoidala hexagonala insättningar).

Besläktade k -enhetliga plattsättningar av vanliga polygoner

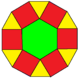
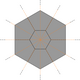
Hexagonerna kan dissekeras i 6 trianglar, och tolvhörningarna kan dissekeras i trianglar, hexagoner och kvadrater.

Dissekerade polygoner
Sexhörning	Dodecagon (var och en har 2 orienteringar)


Dubbla processer (dubbla "insättningar")

3-enhetliga plattsättningar
48	26	18 (2-uniform)
[ ³⁶ ; 3 ² .4.3.4; 3 ² .4.12]	[3,4 ^2,6 ; (3.4.6.4) ² ]	[ ³⁶ ; 3 ² .4.3.4]
V[ ³⁶ ; 3 ² .4.3.4; 3 ² .4.12]	V[3,4 ^2,6 ; (3.4.6.4) ² ]	V[ ³⁶ ; 3 ² .4.3.4]
3-uniforma dualer

Cirkelpackning

Denna 2-enhetliga plattsättning kan användas som en cirkelpackning . Cyancirklar är i kontakt med 3 andra cirklar (2 cyan, 1 rosa), motsvarande V4.6.12-planigonen, och rosa cirklar är i kontakt med 4 andra cirklar (1 cyan, 2 rosa), motsvarande V3.4.6. 4 planigon. Det är homeomorft till ambo-operationen på plattsättningen, med polygonerna cyan och rosa gap som motsvarar de cyan och rosa cirklarna (polygoner med minivertexkonfiguration; endimensionella dubbelgångar till respektive planigoner). Båda bilderna sammanfaller.


C [3.4.6.12]	a[3.4.6.12]

Dubbel plattsättning

Den dubbla plattsättningen har rätvinkliga triangel- och drakeytor , definierade av ansiktskonfigurationer : V3.4.6.4 och V4.6.12, och kan ses kombinera den deltoidala trihexagonala plattsättningen och kisrhombille plattsättningar .

Dubbel plattsättning	V3.4.6.4 V4.6.12	Deltoidal trihexagonal plattsättning	Kisrhombille plattsättning

Anteckningar

Keith Critchlow, Order in Space: A design source book , 1970, s. 62–67
Ghyka, M. The Geometry of Art and Life , (1946), 2:a upplagan, New York: Dover, 1977. Demiregular tiling #15
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X . s. 35–43
Grünbaum, Branko ; Shephard, GC (1987). Kakel och mönster . WH Freeman. ISBN 0-7167-1193-1 . sid. 65
Sacred Geometry Design Sourcebook: Universal Dimensional Patterns , Bruce Rawles, 1997. s. 36–37 [1]

externa länkar

Chavey, D. (1989). "Tilings by Regular Polygons-II: A Catalogue of Tilings" . Datorer och matematik med applikationer . 17 : 147–165. doi : 10.1016/0898-1221(89)90156-9 .
Holländare, Steve. "Uniforma plattor" . Arkiverad från originalet 2006-09-09 . Hämtad 2006-09-09 .
Weisstein, Eric W. "Demiregular tessellation" . MathWorld .
In Search of Demiregular Platings , Helmer Aslaksen
n -uniform plattsättning Brian Galebach, 2-Uniform plattsättning 1 av 20