Viriell expansion

Den klassiska virusexpansionen uttrycker trycket P för ett många-partikelsystem i jämvikt som en potensserie i densiteten :

$$Z\equiv {\frac {P}{RT\rho }}=A+B\rho +C\rho ^{2}+ \cdots$$

där $Z$ kallas kompressibilitetsfaktorn . Detta är den virala tillståndsekvationen, den mest allmänna funktionen som relaterar till tryck, P , densitet, ρ , och temperatur, T , för vätskor. Det föreslogs först av Kamerlingh Onnes . Kompressibilitetsfaktorn är en dimensionslös storhet, som indikerar hur mycket en verklig vätska avviker från en idealgas. A är den första virialkoefficienten, som har ett konstant värde på 1. Den gör påståendet att vid låg densitet beter sig alla vätskor som idealgaser. De viriala koefficienterna B , C , D , etc. är temperaturberoende och presenteras i allmänhet som Taylor-serier i termer av 1/ T .

Andra och tredje viruskoefficienter

Den andra, B , och tredje, C , virial koefficienter har studerats omfattande och tabellerats för många vätskor i mer än ett sekel. Två av de mest omfattande samlingarna finns i Dymonds böcker. och NIST Thermo Data Engine Database och dess Web Thermo Tables. Tabeller över andra och tredje viruskoefficienter för många vätskor ingår i dessa sammanställningar.

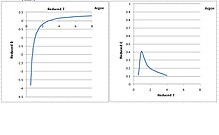
De 2:a och 3:e virialkoefficienterna för argon

De andra och tredje virialkoefficienterna som funktioner av temperatur visas i följande figur för argon. Minskad temperatur och reducerade viruskoefficienter, skalade med respektive kritiska egenskaper, är alla dimensionslösa. Lägg märke till i figuren att den andra virialkoefficienten minskar monotont när temperaturen sänks. Den tredje virialkoefficienten har emellertid en klockform. Den ökar när temperaturen sänks till den kritiska temperaturen, sedan passerar den genom en topp och sjunker snabbt till noll när temperaturen sänks från den kritiska punkten till trippelpunkten. Det är fysiskt orimligt att den sjunker under den kritiska temperaturen. Detta beror på att den tredje virialkoefficienten teoretiskt representerar den frånstötande kraften bland molekyler, som förväntas öka vid en lägre temperatur, när molekyler pressas samman. De beteenden som just beskrivits liknar många andra gaser, som visas i figuren nedan.

Anledningen till att den tredje viruskoefficienten sjunker under den kritiska temperaturen är följande. I allmänhet mäts PρT-isotermerna i gasfasen. Under den kritiska temperaturen kondenserar den gasformiga fasen och samexisterar med vätskefasen, och PρT-isotermen blir platt. Mättnadstrycket ändras inte förrän gasen kondenseras helt till vätska, och sedan stiger trycket när densiteten ökar. Det finns ett stort gap mellan ren gasfas och ren vätskefas där inga användbara tryckdata, förutom mättnadstryck, är tillgängliga. Om endast data i gasfasen analyserades, blir den tredje virialkoefficienten mycket liten, eftersom PρT-isotermen är nästan linjär i gasfasen. Men om datapunkter i den rena vätskefasen inkluderas, skulle en andra ordningens regression ge en stor tredje virial koefficient. Den tredje virialkoefficienten som sålunda härleds skulle öka monotont när temperaturen sänks från den kritiska punkten till trippelpunkten.

Förväntningen att den tredje virialkoefficienten är en monotont ökande funktion av 1/ T kan verifieras med tillståndsekvationer som exakt förutspådde PρT-isotermerna i mättnadsområdet där gasformiga och flytande faser samexisterar.

Gjutning av statens ekvationer till virial form

De flesta tillståndsekvationer kan omformuleras och gjutas i viriala ekvationer för att utvärdera och jämföra deras implicita andra och tredje virialkoefficienter. Van der Waals tillståndsekvation föreslogs 1873:

$$P={\frac {RT}{\left(vb\right)}}-{\frac {a}{v^{2}}}$$

där v = 1/ ρ är molar volym. Det kan ordnas om genom att expandera 1/( v − b ) till en Taylor-serie:

$$Z=1+\left(b-{\frac {a}{RT}}\right)\ rho +b^{2}\rho ^{2}+b^{3}\rho ^{3}+\cdots$$

I Van der Waals ekvation har den andra virialkoefficienten ungefär det korrekta beteendet, eftersom den minskar monotont när temperaturen sänks. De tredje och högre virialkoefficienterna är oberoende av temperatur och är inte korrekta, särskilt vid låga temperaturer.

Nästan alla efterföljande tillståndsekvationer härledda från Van der Waals ekvation, som de från Dieterici, Berthelot, Redlich-Kwong, Peng-Robinson, etc., lider av singulariteten som introduceras av 1/( v - b ) . Därför kan de inte exakt representera PρT-isotermerna vid temperaturer under kritisk temperatur. Många av dem producerar adekvata andra virial koefficienter, men de flesta ger felaktiga tredje virial koefficienter [ .

Andra tillståndsekvationer, startade av Beattie-Bridgeman, är emellertid närmare besläktade med virala ekvationer och visar sig vara mer exakta när det gäller att representera beteendet hos vätskor i både gasformiga och flytande faser. De kan omformuleras till virala tillståndsekvationer och jämföras med varandra. Beattie-Bridgemans statsekvation, som föreslogs 1928,

$$p={\frac {RT}{v^{2}}}\left(1-{\frac {c}{vT^{3}}}\right)(v+B)-{\frac {A}{v^{2}}}$$

var

• $A=A_{0}\left(1-{\frac {a}{v}}\right)$
• $B=B_{0}\left(1-{\frac {b}{v}}\right)$

kan ordnas om:

$$Z=1+ \left(B_{0}-{\frac {A_{0}}{RT}}-{\frac {c}{T^{3}}}\right)\rho -\left(B_{0}b -{\frac {A_{0}a}{RT}}+{\frac {B_{0}c}{T^{3}}}\right)\rho ^{2}+\left({\frac {B_{0}bc}{T^{3}}}\right)\rho ^{3}$$

Denna tillståndsekvation representerar väl den andra virialkoefficienten. Den tredje virialkoefficienten har dock fel tecken. Således misslyckas den med att representera isotermer nära och under den kritiska temperaturen.

Benedict-Webb-Rubins tillståndsekvation från 1940 representerar bättre isotermer under den kritiska temperaturen:

$$Z=1+\left(B_{0}-{\frac {A_{0}}{RT}}-{\frac {C_{0}}{RT^{ 3}}}\right)\rho +\left(b-{\frac {a}{RT}}\right)\rho ^{2}+\left({\frac {\alpha a}{RT}} \right)\rho ^{5}+{\frac {c\rho ^{2}}{RT^{3}}}\left(1+\gamma \rho ^{2}\right)\exp \left (-\gamma \rho ^{2}\right)$$

Fler förbättringar uppnåddes av Starling 1972:

$$Z=1+\left(B_{0}-{\frac {A_{0 }}{RT}}-{\frac {C_{0}}{RT^{3}}}+{\frac {D_{0}}{RT^{4}}}-{\frac {E_{0 }}{RT^{5}}}\right)\rho +\left(b-{\frac {a}{RT}}-{\frac {d}{RT^{2}}}\right)\ rho ^{2}+\alpha \left({\frac {a}{RT}}+{\frac {d}{RT^{2}}}\right)\rho ^{5}+{\frac { c\rho ^{2}}{RT^{3}}}\left(1+\gamma \rho ^{2}\right)\exp \left(-\gamma \rho ^{2}\right)$$

Följande är diagram med reducerade andra och tredje virialkoefficienter mot reducerad temperatur enligt Starling:

2:a och 3:e viruskoefficienterna för 12 vätskor

Exponentialtermerna i de två sista ekvationerna korrigerar den tredje virialkoefficienten så att isotermerna i vätskefasen kan representeras korrekt. Den exponentiella termen konvergerar snabbt när ρ ökar, och om vi bara tog de två första termerna i dess Taylor-expansionsserie, $1-\gamma \rho ^{2}$ , och multiplicera det med $1+\gamma \rho ^{2}$ , resultatet är $1-\gamma ^{2}\rho ^{4}$ . Den bidrar alltså med en $c/RT^{3}$ term till den tredje virialkoefficienten, och en term till den åttonde virialkoefficienten, som kan ignoreras.

Efter expansionen av de exponentiella termerna har Benedict-Webb-Rubin och Starling tillståndsekvationer denna form:

$$Z=1+b\rho _{r}+c\rho _{r}^{2}+f\rho _{r }^{5}$$

De fjärde och femte virialkoefficienterna är noll. Efter den tredje virialtermen är nästa signifikanta term den sjätte virialkoefficienten. Det verkar som om de tre första viriala termerna dominerar komprimeringsfaktorn för vätskor, ner till $0,5T_{c}$ och upp till $2.0\rho _{c}$ .

Omanalys av data av Starling

Om man analyserar data som rapporterats av Starling, representeras virialkoefficienterna bäst av

$$b=b_{0}+{\frac {b_{1}}{t_{r}}}+{\frac {b_{2}}{t_{r}^{2}}}+{\frac {b_{3}}{t_{r}^{3}}}$$

$$c=c_{0}+{\frac {c_{1}}{t_{r}}}+{\frac {c_{2}}{t_{r}^{2}}}+{\frac {c_{3}}{t_{r}^{3}}}$$

$$f=f_{0}+{\frac {f_{1}}{t_{r}}}$$

b och c kunde bestämmas med hjälp av enkel andra ordningens regressionsanalys från experimentella PρT-isotermer. $b_{0}-b_{3}$ och $c_{0}-c_{3}$ kunde sedan bestämmas med hjälp av tredje ordningens regressionsanalys på b och c . $f_{0}-f_{1}$ kan sedan bestämmas genom att analysera rester i komprimerbarhetsfaktor efter att de tre första virialtermerna har tagits bort från den viriala ekvationen. Data från Starling analyseras på nytt och resultaten visas i följande tabell. Dessa koefficienter är alla dimensionslösa, de är alla skalade med kritiska molvolymer och kritisk temperatur.

Vätska	$b_{0}$	$b_{1}$	$b_{2}$	$b_{3}$	$c_{0}$	$c_{1}$	$c_{2}$	$c_{3}$	$f_{0}$	$f_{1}$
Metan	0,440	−1,171	-0,236	-0,210	0,364	-0,275	-0,014	0,396	0,0319	1,71 × 10 −03
Etan	0,330	-0,806	-0,363	-0,378	0,553	-0,675	-0,038	0,680	0,0461	2,63 × 10 −03
Propan	0,288	-0,706	-0,245	-0,575	0,532	-0,546	-0,308	0,843	0,0334	1,89 × 10 −02
n-butan	0,377	-0,916	-0,115	-0,610	0,547	-0,519	-0,347	0,871	0,0305	2,04 × 10 −02
i-Butan	0,438	−1,051	-0,172	-0,401	0,483	-0,342	-0,021	0,538	0,0194	1,19 × 10 −03
n-pentan	0,481	−1,056	-0,166	-0,560	0,668	-0,720	−0,204	0,841	0,0411	1,17 × 10 −02
i-Pentan	0,242	-0,674	-0,306	-0,520	0,815	-0,943	−0,194	0,868	0,0484	9,99 × 10 −03
n-hexan	0,435	-0,636	-0,358	-0,759	0,848	−1,275	-0,105	1,120	0,0604	4,98 × 10 −03
n-heptan	0,493	-0,798	-0,636	-0,428	0,589	-0,738	-0,017	0,814	0,0508	1,21 × 10 −03
n-oktan	0,600	-0,744	-0,456	-0,763	0,174	−0,197	-0,272	0,919	0,0144	1,99 × 10 −02
Kväve	0,502	−1,380	0,092	-0,333	0,400	-0,276	-0,027	0,322	0,0279	2,72 × 10 −03
CO 2	0,178	-0,044	−1,517	0,039	0,428	-0,422	-0,008	0,687	0,0490	9,52 × 10 −04
H 2 S	0,191	-0,927	-0,078	-0,366	1,093	−1,227	-0,001	0,577	0,0578	8,37 × 10 −05

Kubisk virial statsekvation

Treterm virial ekvation eller en kubisk virial tillståndsekvation

$$Z=1+B\rho +C\rho ^{2}$$

har enkelheten hos Van der Waals tillståndsekvation utan dess singularitet vid v = b . Teoretiskt representerar den andra virialkoefficienten bimolekylära attraktionskrafter, och den tredje virialtermen representerar de repulsiva krafterna bland tre molekyler i nära kontakt. Intuitivt bör vi förvänta oss att B blir negativ vid låg temperatur, medan C skulle förbli positiv för att motverka effekten av B och pressar Z och därmed trycket till höga värden när ρ ökar.

Med denna kubiska virala ekvation kan koefficienterna B och C lösas i sluten form. Att införa de kritiska villkoren:

$${\frac {\mathrm {d} P}{\mathrm {d} v}}=0\qquad {\text{and}}\qquad { \frac {\mathrm {d} ^{2}P}{\mathrm {d} v^{2}}}=0$$

den kubiska virala ekvationen kan lösas för att ge:

$$B=-v_{c},$$

$$C={\frac {v_{c}^{2}}{3}},$$

och

$$Z_{c}={\frac {P_{c}v_{c}}{RT_{c}}}={\frac {1}{3}}.$$

$Z_{c}$ är därför 0,333, att jämföra med 0,375 från Van der Waals tillståndsekvation.

Mellan den kritiska punkten och trippelpunkten finns mättnadsområdet för vätskor. I detta område samexisterar gasfasen med vätskefasen under mättnadstryck $P_{\text{sat}}$ och mättnadstemperaturen $T_{\text{sat}}$ . Under mättnadstrycket har vätskefasen en molvolym på $v_{\text{l}}$ och den gasformiga fasen har en molarvolym på $v_{\text{g}}$ . Motsvarande molartätheter är $\rho _{\text{l}}$ och $\rho _{\text{g}}$ . Dessa är de mättnadsegenskaper som behövs för att beräkna andra och tredje virialkoefficienter.

En giltig tillståndsekvation måste producera en isoterm som korsar den horisontella linjen för $P_{\text{sat}}$ vid $v_{\text{l}}$ och $v_{\text{g}}$ , på $T_{\text{sat}}$ . Under $P_{\text{sat}}$ och $T_{\text{sat}}$ är gasen i jämvikt med vätska. Detta betyder att PρT-isotermen har tre rötter vid $P_{\text{sat}}$ . Den kubiska virala tillståndsekvationen vid $T_{\text{sat}}$ är:

$$P_{\text{sat}}=RT_{\text{sat}}\left(1+B\rho +C\rho ^ {2}\right)\rho$$

Det kan arrangeras om som:

$$1-{\frac {RT_{\text{sat}}}{P_{\text{sat}}}}\left (1+B\rho +C\rho ^{2}\right)\rho =0$$

Faktorn $RT_{\text{sat}}/P_{\text{sat}}$ är volymen av mättad gas enligt den ideala gaslagen, och kan ges ett unikt namn $v^{\text{id}}$ :

$$v^{\text{id}}={\frac {RT_{\text{sat}}}{P_{\text{sat}}}}$$

I mättnadsområdet har den kubiska ekvationen tre rötter och kan skrivas alternativt som:

$$\left(1-v_{\text{l}}\rho \right)\left(1-v_{ \text{m}}\rho \right)\left(1-v_{\text{g}}\rho \right)=0$$

som kan utökas som:

$$1-\left( v_{\text{l}}+v_{\text{g}}+v_{m}\right)\rho +\left(v_{\text{l}}v_{\text{g}}+v_{ \text{g}}v_{\text{m}}+v_{\text{m}}v_{\text{l}}\right)\rho ^{2}-v_{\text{l}}v_ {\text{g}}v_{\text{m}}\rho ^{3}=0$$

$v_{\text{m}}$ är en volym av ett instabilt tillstånd mellan $v_{\text{l}}$ och $v_{\text{g}}$ . Kubikekvationerna är identiska. Därför, från de linjära termerna i dessa ekvationer, $v_{m}$ lösas:

$$v_{\text{m}}=v^{\text{id}}-v_{\text{l}}-v_{\text{g}}$$

Från de kvadratiska termerna kan B lösas:

$$B=-{\frac {\left(v_{\text{l}}v_{\text{g}} +v_{\text{g}}v_{\text{m}}+v_{\text{m}}v_{\text{l}}\right)}{v^{\text{id}}}}$$

Och från kubiktermerna kan C lösas:

$$C={\frac {v_{\text{l}}v_{\text{g}}v_{\text{m}}}{v^{\text {id}}}}$$

Eftersom $v_{\text{l}}$ , $v_{\text{g}}$ och $P_{\text{sat}}$ har tabellerats för många vätskor med $T_{\text{sat}}$ som parameter, B och C kan beräknas i mättnadsområdet för dessa vätskor. Resultaten överensstämmer i allmänhet med de som beräknats från Benedict-Webb-Rubin och Starlings statsekvationer. Men noggrannheten i B och C är kritiskt beroende av måtten $v_{\text{g}}$ och ${\displaystyle P_{\text{sat}}} ,$ vilket är mycket svåra att mäta exakt vid låga temperaturer. Mätfelen som sålunda introducerats i B och C bör beaktas när man jämför de sålunda härledda värdena med de som härleds från andra ordningens regressionsanalys av PρT-isotermer.

Gas-vätska-fast jämvikt

Den kubiska virala tillståndsekvationen representerar exakt gas-vätskejämvikten för det mesta ämnet från den kritiska punkten ner till trippelpunkten, där fast fas börjar dyka upp. Det kan utökas för att ta hänsyn till gas-vätska-fast jämvikt:

$$P={\frac {RT}{V}}\left(1+{\frac {B} {V}}+{\frac {C}{V^{2}}}+{\frac {U}{V^{n}}}+{\frac {W}{V^{2n}}}\ höger)$$

I denna ekvation representerar den första termen ${\textstyle {\frac {RT}{V}}}$ trycket som genereras av molekylers kinetiska Den andra termen ${\textstyle {\frac {RTB}{V^{2}}}}$ representerar långväga bimolekylär attraktion. Den tredje termen ${\textstyle {\frac {RTC}{V^{3}}}}$ representerar kortdistans tri-molekylär repulsion. Den andra termen drar ner PVT-isotermen när volymen minskar, medan den tredje termen driver isotermen uppåt. När temperaturen är under den kritiska punkten har PVT-isotermen således en S-formad böjning som tillåter en flytande fas att samexistera med den rådande gasfasen.

Om vi ​​nu hade en ${\textstyle {\frac {RTU}{V^{n}}}}$ term för att dra ner PVT-isotermen i vätskefasen, och en ${ \textstyle {\frac {RTW}{V^{2n}}}}$ termer för att trycka upp den igen, kan en fast fas skapas, eftersom dessa två termer ger en annan S-formad böjning mellan flytande och fast substans. Det visades att en sådan S-formad böj kunde syntetiseras med hjälp av en $\delta$ -funktion som Lorentzian funktion över en van der Waals tillståndsekvation. En sådan tillståndsekvation är svår att manipulera matematiskt. Däremot är en virial ekvation lättare att hantera.

Argon används för att realistiskt utvärdera denna utökade viriala ekvation för gas-vätska-fast jämvikt. Data kommer att analyseras i reducerade former. Alla PVT-variabler skalas med sina respektive kritiska värden. Det förväntas av principen för motsvarande tillstånd att resultaten skulle gälla andra väluppfostrade vätskor. Relevanta data för argon sammanfattas i följande tabell:

Argons egendom	Värde	Minskat värde
Kritisk punktvolym (dm 3 /mol)	0,07459	1
Kritisk punkttemperatur (K)	150,687	1
Kritiskt punkttryck (MPa)	4,863	1
Kritisk kompressibilitet	0,291	0,291
Trepunkts ångvolym (dm 3 /mol)	9,853	132,1
Trippelpunkts vätskevolym (dm 3 /mol)	0,0282	0,378
Trepunkts fast molarvolym (dm 3 /mol)	0,246	0,330
Trippelpunktstemperatur (K)	83,8058	0,553
Trippelpunktstryck (MPa)	0,06889	0,0142

När variablerna P , V och T ersätts med deras reducerade ekvivalenter, ${\textstyle p={\frac {P}{P_{c}}}}$ , ${\textstyle v ={\frac {V}{V_{c}}}}$ och ${\textstyle t={\frac {T}{T_{c}}}} ,$ den viriala ekvationen har följande form:

$$p={\frac {t}{vZ_{c}}}\ vänster(1-{\frac {b}{v}}+{\frac {c}{v^{2}}}-\left({\frac {v_{u}}{v}}\right)^ {n}+\left({\frac {v_{w}}{v}}\right)^{2n}\right)$$

där ${\textstil Z_{c}={\frac {P_{c}V_{c}}{RT_{c}}}} , b =$ B $b ={\frac {B}{V_{c}}}}$ , ${\textstyle c={\frac {C}{V_{c}^{2}}}}$ , ${\textstyle U=v_{u}^{n}}$ och ${\textstyle W=v_{w}^{2n}}$ . Vi kommer att ägna oss mest åt tillståndet vid argons trippelpunkt, där b = 3,424 och c = 1,152 från en tidigare studie.

$V_{w}$ måste vara något större än volymen av fast argon, 0,33, och $v_{u}$ måste vara mellan volymerna av flytande och fast argon. Initialt ställs ${\displaystyle v_{w}} in på volymen av fast material för att producera den sista kraftigt stigande kanten av isotermen där fast fas uppträder vid mycket låg volym.$ Det exponentiella n måste sedan bestämmas så att dalen i n -2 n potentialen måste passa mellan volymerna fast (0,33) och vätska (0,378). Efter att exponentiellt n har bestämts kan värdet på $v_{u}$ justeras för att uppfylla Gibbs-regeln, som kräver att Gibbs fria energi för flytande fas och den för fast fas måste vara lika under trippeln punkttemperatur och tryck.

För att producera en fast fas i argon måste exponentialvärdet n vara mycket stort, större än 20; annars skulle PVT-isotermen inte böjas till en S-form mellan flytande och fast substans. Den bästa uppskattningen är att n = 30, ${\displaystyle t_{t}=0,553} ,$ v $\displaystyle v_{w}=0,335}$ och $v_{u }=0,3443$ . Isotermen visas i den högra figuren, där tre virial termer är ritade separat för tydlighetens skull:

$$p_{1}={\frac {t_{t}}{vZ_{c}}}\left(1-{\frac {b}{v}}+{\frac {c}{v^{2}}}\right)$$

$$p_{2}={\frac {t_{t}}{vZ_{c}}}\left({\frac {v_{u}} {v}}\right)^{n}$$

$$p_{3}={\frac {t_{t}}{vZ_{c}}}\left({\frac {v_{w} }{v}}\right)^{2n}$$

$$p=p_{1}-p_{2}+p_{3}$$

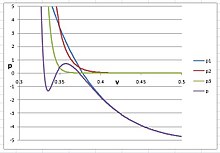
PVT-isoterm av argon med n = 30 .

I den här figuren representerar $p_{1}$ summan av de tre första viriala termerna, i den kubiska viriala ekvationen, och den visar beteendet hos argon i dess gasformiga och flytande faser. $p_{2}$ representerar potentialen från termen ( $\textstyle \left({\frac {v_{u}}{v}}\right)^{n}}$ , och $p_{3}$ representerar bidragen från ${\textstyle \left({\frac {v_{w}}{v}}\right)^{2n} }$ term. När n < 30, skulle $p_{2}$ störa $p_{1}$ och sänka volymen av vätska avsevärt.

Det är överraskande att n måste vara större än 20 för att producera en fast fas. Det är välkänt att Lenard-Jones 6-12 potentialen kan användas för att beräkna den andra virialkoefficienten från kvantmekaniska principer. Kvantmekaniskt resonemang relaterar den andra viriala koefficienten till bimolekylär attraktion, och den tredje koefficienten till tri-molekylär repulsion, etc. I argons flytande fas är en atom omgiven av 12 närmaste grannar och upp till 32 närmaste grannar. I den fasta fasen är alla atomer låsta på plats, och antalet interagerande grannar är oändligt. Därför n = 30, eller ännu större, rimligt.

Som ett resultat har vi en viriell tillståndsekvation för att kvantitativt beskriva gas-vätska-fast jämvikt för argon och alla vätskor som följer principen för motsvarande tillstånd, vid dess trippelpunkt:

$$p={\frac {t_{t}}{vZ_{c}}} \left(1-{\frac {3.424}{v}}+{\frac {1.152}{v^{2}}}-\left({\frac {0.3443}{v}}\right)^{30 }+\left({\frac {0.3350}{v}}\right)^{60}\right)$$

Viriala tillståndsekvationer

Från Benedict-Webb-Rubin och Starlings tillståndsekvationer bestämdes det att den bästa viriala tillståndsekvationen skulle ha formen av [

$$Z=1+b\rho _{r}+c\rho _{r}^{2}+f\rho _{r}^{5}.$$

De andra och tredje virialkoefficienterna i denna ekvation kan beräknas från experimentella PρT-data med hjälp av en linjär regression . Efter att ha tagit bort de första tre viriala termerna kunde resten i kompressibilitetsfaktor Z sedan användas för att erhålla den sjätte viruskoefficienten.

Se även

• Virial teorem
• Statistisk mekanik
• Tillståndsekvation