Sperners lemma

Det tvådimensionella fallet med Sperners lemma: en Sperner-färgning, med sina trefärgade trianglar skuggade

Inom matematik är Sperners lemma ett kombinatoriskt resultat på färgningar av trianguleringar , analogt med Brouwers fixpunktssats, som motsvarar den. Den anger att varje Sperner-färgning (beskrivs nedan) av en triangulering av en $n$ -dimensionell simplex innehåller en cell vars hörn alla har olika färger.

Det första resultatet av detta slag bevisades av Emanuel Sperner , i samband med bevis på invarians av domän . Sperner-färger har använts för effektiv beräkning av fixpunkter och i rotsökningsalgoritmer och används i algoritmer för rättvis division (kakskärning). Att hitta en Sperner-färgning eller motsvarande en Brouwer fast punkt tros nu vara ett svårlöst beräkningsproblem, även i flygplanet, i det allmänna fallet. Problemet är PPAD-komplett , en komplexitetsklass uppfunnen av Christos Papadimitriou .

Enligt Soviet Mathematical Encyclopaedia (red. IM Vinogradov ) hade en relaterad sats från 1929 (av Knaster , Borsuk och Mazurkiewicz ) också blivit känd som Sperner-lemmat – denna punkt diskuteras i den engelska översättningen (red. M. Hazewinkel). Det är nu allmänt känt som Knaster–Kuratowski–Mazurkiewicz-lemmat .

Påstående

Endimensionell låda

Endimensionellt fall exempel

I en dimension kan Sperners Lemma betraktas som en diskret version av mellanvärdessatsen . I det här fallet säger det i huvudsak att om en diskret funktion endast tar värdena 0 och 1, börjar vid värdet 0 och slutar vid värdet 1, så måste den byta värden ett udda antal gånger.

Tvådimensionell låda

Det tvådimensionella fallet är det som hänvisas till oftast. Det står så här:

Dela upp en triangel $ABC$ godtyckligt i en triangulering som består av mindre trianglar som möts kant i kant. Då definieras en Sperner-färgning av trianguleringen som en tilldelning av tre färger till trianguleringens hörn så att

Var och en av de tre hörnen $A$ , $B$ och $C$ i den initiala triangeln har en distinkt färg
De hörn som ligger längs någon kant av triangeln $ABC$ har bara två färger, de två färgerna vid kantens ändpunkter. Till exempel måste varje vertex på $AC$ ha samma färg som $A$ eller $C$ .

Sedan har varje Sperner-färgning av varje triangulering minst en "regnbågstriangel", en mindre triangel i trianguleringen som har sina hörn färgade med alla tre olika färger. Mer exakt måste det finnas ett udda antal regnbågstrianglar.

Flerdimensionell låda

I det allmänna fallet hänvisar lemmat till ett $n-$ dimensionellt simplex :

{\mathcal {A}}=A_{1}A_{2}\ldots A_{n+1}.

Betrakta vilken triangulering som helst $T$ , en disjunkt uppdelning av ${\mathcal {A}}$ i mindre $n$ -dimensionella förenklingar, som återigen möts ansikte mot ansikte. Beteckna färgningsfunktionen som:

f:S\to \{1,2,3,\dots ,n,n+1\},

där $S$ är mängden av hörn av $T$ . En färgningsfunktion definierar en Sperner-färgning när:

Topparna på den stora simplexen är färgade med olika färger, dvs $f (A i) = i$ för $1 < i < n + 1$ .
Vertices av $T$ placerade på någon $k$ -dimensionell underyta av den stora simplexen
$A_{i_{1}}A_{i_{2}}\ldots A_{i_{k+1}}$

färgas endast med färgerna

$i_{1},i_{2},\ldots ,i_{k+1}.$

Sedan har varje Sperner-färgning ett udda antal förenklingar sin triangulering, vars hörn är färgade med alla $n + 1$ färger. I synnerhet måste det finnas minst en regnbågssimplex.

Bevis

En slumpmässig Sperner-färgning av en vanlig triangularisering. Varje återvändsgränd är en RGB-triangel

Vi ska först ta upp det tvådimensionella fallet. Betrakta en graf $G$ byggd från trianguleringen $T$ enligt följande:

Topparna av

G

är medlemmarna av

T

plus området utanför triangeln. Två hörn är förbundna med en kant om deras motsvarande områden delar en gemensam gräns med den ena ändpunkten färgad 1 och den andra färgad 2.

Observera att på intervallet $AB$ finns det ett udda antal kantlinjer färgade 1-2 (helt enkelt för att A är färgad 1, B är färgad 2; och när vi rör oss längs $AB$ måste det finnas ett udda antal färgbyten för att få olika färger i början och i slutet). Därför har $G-$ punkten som motsvarar ytterområdet en udda grad. Men det är känt ( handskakningslemma ) att det i en finit graf finns ett jämnt antal hörn med udda grad. Därför har den återstående grafen, exklusive det yttre området, ett udda antal hörn med en udda grad som motsvarar medlemmar av $T$ .

Det kan lätt ses att den enda möjliga graden av en triangel från $T$ är 0, 1 eller 2, och att graden 1 motsvarar en triangel färgad med de tre färgerna 1, 2 och 3.

Därmed har vi fått en något starkare slutsats, som säger att det i en triangulering $T$ finns ett udda antal (och minst en) fullfärgade trianglar.

Ett flerdimensionellt fall kan bevisas genom induktion på dimensionen av en simplex. Vi tillämpar samma resonemang, som i det tvådimensionella fallet, för att dra slutsatsen att det i en $n$ -dimensionell triangulering finns ett udda antal fullfärgade förenklingar.

Kommentar

En enkel tvådimensionell triangulering av exempelfiguren, färgad och namngiven i enlighet med antagandena i Sperners Lemma

Grafen härledd från exempelfiguren

Här är en fördjupning av beviset som gavs tidigare, för en läsare som är ny inom grafteorin .

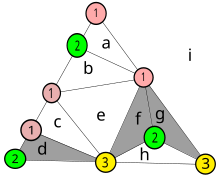
Detta diagram numrerar färgerna på hörnen i exemplet som gavs tidigare. De små trianglarna vars hörn alla har olika nummer är skuggade i grafen. Varje liten triangel blir en nod i den nya grafen som härrör från trianguleringen. De små bokstäverna identifierar områdena, åtta inuti figuren, och område $i$ betecknar utrymmet utanför den.

Som beskrivits tidigare sammanfogas de noder som delar en kant vars ändpunkter är numrerade 1 och 2 i den härledda grafen. Till exempel delar nod $d en kant med det yttre området$ $i$ , och dess hörn har alla olika nummer, så den är också skuggad. Nod $b$ är inte skuggad eftersom två hörn har samma nummer, men den är sammanfogad med det yttre området.

Man skulle kunna lägga till en ny fullnumrerad triangel, t.ex. genom att infoga en nod numrerad 3 i kanten mellan 1 och 1 av nod a, $och$ förena den noden med den andra vertexen av $a$ . Om du gör det måste du skapa ett par nya noder, som situationen med noderna $f$ och $g$ .

Generaliseringar

Underuppsättningar av etiketter

Antag att varje vertex i trianguleringen kan märkas med flera färger, så att färgningsfunktionen är $F : S \to 2 [n +1]$ .

För varje sub-simplex är uppsättningen etiketter på dess hörn en uppsättning-familj över uppsättningen av färger [ $n + 1]$ . Denna uppsättningsfamilj kan ses som en hypergraf .

Om färgerna i $f (v) för varje vertex$ $v på en yta av simplexen$ är en delmängd av färguppsättningen på ytans ändpunkter, så finns det en sub-simplex med en balanserad märkning – en märkning där motsvarande hypergraf medger en perfekt bråkmatchning . För att illustrera, här är några balanserade märkningsexempel för $n = 2$ :

$({1}, {2}, {3})$ - balanseras av vikterna $(1, 1, 1)$ .
$({1,2}, {2,3}, {3,1})$ - balanseras av vikterna $(1/2, 1/2, 1/2)$ .
$({1,2}, {2,3}, {1})$ - balanserad av vikterna $(0, 1, 1)$ .

Detta bevisades av Shapley 1973. Det är en kombinatorisk analog till KKMS-lemmat .

Polytopala varianter

Antag att vi har en $d$ -dimensionell polytop $P$ med $n$ hörn. $P$ trianguleras och varje vertex av trianguleringen är märkt med en etikett från ${1, \dots, n}.$ Varje huvudpunkt $i$ är märkt med $i$ . En sub-simplex kallas fullständigt märkt om den är $d$ -dimensionell, och var och en av dess $d + 1$ hörn har en annan etikett. Om varje vertex i en yta $F$ av $P$ är märkt med en av etiketterna på ändpunkterna av $F$ , så finns det åtminstone $n - d$ fullständigt märkta förenklingar. Några speciella fall är:

$d = n - 1$ . I detta fall är $P en simplex.$ Det polytopala Sperner-lemmat garanterar att det finns minst 1 helt märkt simplex. Det vill säga, det reducerar till Sperners lemma.
$d = 2$ . Antag att en tvådimensionell polygon med $n$ hörn trianguleras och märks med beteckningarna $1, \dots, n$ så att, på varje sida mellan vertex $i$ och vertex $i + 1 (mod n)$ , endast etiketterna $i$ och $i + 1$ används . Sedan finns det minst $n - 2$ undertrianglar där tre olika etiketter används.

Det allmänna uttalandet antogs av Atanassov 1996, som bevisade det för fallet $d = 2$ . Beviset för det allmänna fallet gavs först av de Loera, Peterson och Su 2002. De ger två bevis: det första är icke-konstruktivt och använder begreppet småstensuppsättningar ; den andra är konstruktiv och bygger på argument för att följa banor i grafer .

Meunier utökade satsen från polytoper till polytopala kroppar, som inte behöver vara konvexa eller enkelt sammankopplade. I synnerhet, om $P$ är en polytop, är uppsättningen av dess ytor en polytopal kropp. I varje Sperner-märkning av en polytopal kropp med hörn $v 1, \dots, v n$ , finns det åtminstone:

nd-1+\left\lceil {\frac {\min _{i=1}^{n }\deg _{B(P)}(v_{i})}{d}}\right\rceil

helt märkta förenklingar så att vilket par som helst av dessa förenklingar får två olika märkningar. Graden $deg B (P) (v i)$ är antalet kanter på $B (P)$ som $v i$ tillhör. Eftersom graden är minst $d$ är den nedre gränsen minst $n - d$ . Men den kan vara större. Till exempel, för den cykliska polytopen i 4 dimensioner med $n$ hörn, är den nedre gränsen:

n-4-1+\left\lceil {\frac {n-1}{4}}\right\rceil \approx {\frac {5}{4}}n.

Musin utökade satsen ytterligare till $d$ -dimensionella styckvis-linjära grenrör , med eller utan en gräns.

Asada, Frick, Pisharody, Polevy, Stoner, Tsang och Wellner utökade satsen ytterligare till pseudomanifolder med gräns, och förbättrade den nedre gränsen för antalet fasetter med parvis distinkta etiketter.

Kubiska varianter

Antag att vi, istället för en simplex triangulerad till sub-simplices, har en $n$ -dimensionell kub uppdelad i mindre $n$ -dimensionella kuber.

Harold W. Kuhn bevisade följande lemma. Antag att kuben $[0, M] n$ , för något heltal $M$ , är uppdelad i $M n$ enhetskuber. Antag att varje hörn av partitionen är märkt med en etikett från ${1, \dots, n + 1},$ så att för varje vertex $v$ : (1) om $v i = 0$ så är etiketten på $v$ som mest $i$ ; (2) om $v i = M$ så är etiketten på $v$ inte $i$ . Sedan finns det en enhetskub med alla etiketterna ${1, \dots, n + 1}$ (några av dem mer än en gång). Specialfallet $n = 2$ är: anta att en kvadrat är uppdelad i delkvadrater och varje hörn är märkt med en etikett från { $1,2,3}.$ Den vänstra kanten är märkt med $1$ (= högst 1); den nedre kanten är märkt med $1$ eller $2$ (= högst 2); den övre kanten är märkt med $1$ eller $3$ (= inte 2); och den högra kanten är märkt med $2$ eller $3$ (= inte 1). Sedan finns det en kvadrat märkt med $1,2,3.$

En annan variant, relaterad till Poincaré-Miranda-satsen , är följande. Antag att kuben $[0, M] n$ är uppdelad i $M n$ enhetskuber. Antag att varje vertex är märkt med en binär vektor med längden $n$ , så att för varje vertex $v$ : (1) om $v i = 0$ så är koordinaten $i$ för etiketten på $v$ 0; (2) om $vi; = M$ så är koordinaten $i$ för etiketten på $v$ 1 (3) om två hörn är grannar, skiljer sig deras etiketter med högst en koordinat. Sedan finns det en enhetskub där alla $2 n$ etiketter är olika. I två dimensioner är ett annat sätt att formulera denna sats: i varje märkning som uppfyller villkoren (1) och (2), finns det minst en cell där summan av etiketter är 0 [en 1-dimensionell cell med (1 $, 1)$ och $(-1,-1)$ etiketter, eller en 2-dimensionell cell med alla fyra olika etiketter].

Wolsey stärkte dessa två resultat genom att bevisa att antalet helt märkta kuber är udda.

Musin utvidgade dessa resultat till allmänna fyrlingar .

Regnbågsvarianter

Antag att vi istället för en enda märkning har $n$ olika Sperner-märkningar. Vi betraktar par (simplex, permutation) så att etiketten för varje hörn av simplexen väljs från en annan märkning (så för varje simplex finns det n ! $olika par$ ). Då finns det åtminstone $n!$ helt märkta par. Detta bevisades av Ravindra Bapat för varje triangulering. Ett enklare bevis, som bara fungerar för specifika trianguleringar, presenterades senare av Su.

Ett annat sätt att uttrycka detta lemma är följande. Anta att det finns $n$ personer, som var och en producerar olika Sperner-märkning av samma triangulering. Sedan finns det en simplex och en matchning av personerna till dess hörn, så att varje vertex märks på olika sätt av sin ägare (en person etiketterar dess vertex med 1, en annan person märker dess vertex med 2, etc.). Dessutom finns det minst $n!$ sådana matchningar. Detta kan användas för att hitta en avundsfri tårtskärning med sammankopplade bitar.

Asada, Frick, Pisharody, Polevy, Stoner, Tsang och Wellner utökade denna sats till pseudomanifolds med gräns.

Antag mer generellt att vi har $m$ olika Sperner-märkningar, där $m$ kan vara annorlunda än $n$ . Sedan:

För alla positiva heltal $k 1, \dots, k m$ vars summa är $m + n - 1$ , finns det en baby-simplex där, för varje $i \in {1, \dots, m},$ märkningsnummer $i$ använder minst $k i$ ( av $n$ ) distinkta etiketter. Dessutom används varje etikett av minst en (av $m$ ) märkning.
För alla positiva heltal $I 1, \dots, I m$ vars summa är $m + n - 1$ , finns det en baby-simplex där, för varje $j \in {1, \dots, n},$ , används etiketten $j$ av minst $l j$ (av $m$ ) olika märkningar.

Båda versionerna reduceras till Sperners lemma när $m = 1$ , eller när alla $m$ märkningar är identiska.

Se för liknande generaliseringar.

Orienterade varianter

Sekvens	Grad
123	1 (en 1-2-brytare och ingen 2-1-brytare)
12321	0 (en 1-2-brytare minus en 2-1-brytare)
1232	0 (som ovan; återkallningssekvensen är cyklisk)
1231231	2 (två 1-2-brytare och ingen 2-1-brytare)

Brown och Cairns stärkte Sperners lemma genom att överväga inriktningen av enkla. Varje sub-simplex har en orientering som kan vara antingen +1 eller -1 (om den är helt märkt) eller 0 (om den inte är helt märkt). De bevisade att summan av alla orienteringar av simpliceringar är +1. I synnerhet innebär detta att det finns ett udda antal helt märkta förenklingar.

Som ett exempel för $n = 3$ , anta att en triangel är triangulerad och märkt med ${1,2,3}.$ Betrakta den cykliska sekvensen av etiketter på triangelns gräns. Definiera graden av märkning som antalet switchar från 1 till 2, minus antalet switchar från 2 till 1. Se exempel i tabellen till höger. Observera att graden är densamma om vi räknar växlar från 2 till 3 minus 3 till 2, eller från 3 till 1 minus 1 till 3.

Musin bevisade att antalet helt märkta trianglar är åtminstone graden av märkningen . I synnerhet, om graden inte är noll, så finns det åtminstone en helt märkt triangel.

Om en märkning uppfyller Sperner-villkoret är dess grad exakt 1: det finns 1-2 och 2-1 omkopplare endast i sidan mellan hörn 1 och 2, och antalet 1-2 omkopplare måste vara en mer än antalet av 2-1 omkopplare (när man går från vertex 1 till vertex 2). Därför följer det ursprungliga Sperner-lemmat av Musins sats.

Träd och cykler

Det finns ett liknande lemma om ändliga och oändliga träd och cykler .

Relaterade resultat

Mirzakhani och Vondrak studerar en svagare variant av en Sperner-märkning, där det enda kravet är att etikett i inte används på ansiktet mitt emot vertex i . De kallar det Sperner-tillåten märkning . De visar att det finns Sperner-godkända märkningar där varje cell innehåller högst 4 etiketter. De visar också en optimal nedre gräns för antalet celler som måste ha minst två olika märkningar i varje Sperner-tillåten märkning. De bevisar också att, för varje Sperner-tillåten partition av den vanliga simplexen, den totala arean av gränsen mellan delarna minimeras av Voronoi-partitionen .

Ansökningar

Sperner-färger har använts för effektiv beräkning av fixpunkter . En Sperner-färgning kan konstrueras så att helt märkta förenklingar motsvarar fasta punkter för en given funktion. Genom att göra en triangulering mindre och mindre kan man visa att gränsen för de helt märkta förenklingarna är exakt den fasta punkten. Därför ger tekniken ett sätt att approximera fasta punkter. En relaterad tillämpning är numerisk detektering av periodiska banor och symbolisk dynamik . Sperners lemma kan också användas i rotsökningsalgoritmer och algoritmer för rättvis division ; se Simmons–Su-protokoll .

Sperners lemma är en av nyckelingredienserna i beviset för Monskys sats , att en kvadrat inte kan skäras till ett udda antal trianglar med lika yta .

Sperners lemma kan användas för att hitta en konkurrenskraftig jämvikt i en utbytesekonomi , även om det finns mer effektiva sätt att hitta den.

Femtio år efter att ha publicerat den första gången presenterade Sperner en undersökning om utvecklingen, inflytandet och tillämpningarna av sitt kombinatoriska lemma.

Motsvarande resultat

Det finns flera fixpunktssatser som finns i tre ekvivalenta varianter: en algebraisk topologivariant , en kombinatorisk variant och en mängdtäckande variant. Varje variant kan bevisas separat med helt olika argument, men varje variant kan också reduceras till de andra varianterna i sin rad. Dessutom kan varje resultat i den översta raden härledas från det under det i samma kolumn.

Algebraisk topologi	Kombinatorik	Set täckning
Brouwers fixpunktssats	Sperners lemma	Knaster–Kuratowski–Mazurkiewicz lemma
Borsuk–Ulams teorem	Tuckers lemma	Lusternik–Schnirelmanns sats

Se även

Topologisk kombinatorik

externa länkar

Bevis på Sperners Lemma vid cut-the-knot
Sperners lemma och triangelspelet , på den n-rika platsen.
Sperners lemma i 2D , ett webbaserat spel på itch.io.