Ormlemma

Ormlemma är ett verktyg som används i matematik , särskilt homologisk algebra , för att konstruera långa exakta sekvenser . Ormlemmat är giltigt i alla abelska kategorier och är ett avgörande verktyg i homologisk algebra och dess tillämpningar, till exempel i algebraisk topologi . Homomorfismer konstruerade med dess hjälp kallas allmänt för sammanbindande homomorfismer .

Påstående

I en abelsk kategori (som kategorin abelska grupper eller kategorin vektorrum över ett givet fält ), överväg ett kommutativt diagram :

där raderna är exakta sekvenser och 0 är nollobjektet .

Sedan finns det en exakt sekvens som relaterar till kärnorna och kokkärnorna i a , b och c :

$\ker a~{\color {Gray}\longrightarrow }~\ker b~{\color {Gray }\longrightarrow }~\ker c~{\overset {d}{\longrightarrow }}~\operatörsnamn {coker} a~{\color {Grå}\longrightarrow }~\operatörsnamn {coker} b~{\color {Grå }\longrightarrow }~\operatörsnamn {coker} c$

där d är en homomorfism, känd som den anslutande homomorfismen .

Dessutom, om morfismen f är en monomorfism , så är morfismen ${\displaystyle \ker a~{\color {Gray}\longrightarrow }~\ker b} ,$ och om g' är en epimorfism , då är det även $\operatorname {coker} b~{\color {Gray}\longrightarrow }~\operatörsnamn {coker} c$ .

Kokarna här är: ${\displaystyle \operatorname {coker} a=A'/\operatörsnamn {im} a} ,$ coker $\displaystyle \ operatörsnamn {coker} b=B'/\operatörsnamn {im} b}$ , $\operatorname {coker} c=C'/\operatörsnamn {im} c$ .

Förklaring av namnet

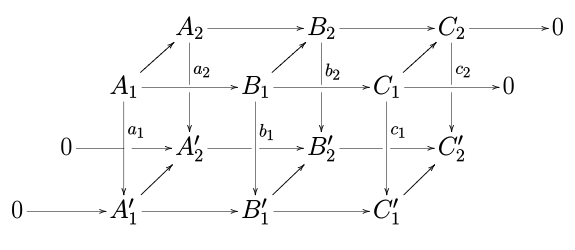
För att se var ormlemmat får sitt namn, expandera diagrammet ovan enligt följande:

och sedan kan den exakta sekvensen som är slutsatsen av lemma dras på detta utökade diagram i den omvända "S"-formen av en glidande orm .

Konstruktion av kartorna

En animering av kartans konstruktion d

Kartorna mellan kärnorna och kartorna mellan kokkärnorna induceras på ett naturligt sätt av de givna (horisontella) kartorna på grund av diagrammets kommutativitet. Exaktheten hos de två inducerade sekvenserna följer på ett enkelt sätt av exaktheten hos raderna i det ursprungliga diagrammet. Lemmats viktiga påstående är att det finns en sammanbindande homomorfism d som fullbordar den exakta sekvensen.

I fallet med abelska grupper eller moduler över någon ring kan kartan d konstrueras enligt följande:

Välj ett element x i ker c och se det som ett element av C ; eftersom g är surjektiv finns det y i B med g ( y ) = x . På grund av kommutativiteten i diagrammet har vi g' ( b ( y )) = c ( g ( y )) = c ( x ) = 0 (eftersom x är i kärnan av c ), och därför b ( y ) är i kärnan av g' . Eftersom den nedre raden är exakt hittar vi ett element z i A' med f '( z ) = b ( y ). z är unik genom injektiviteten av f '. Vi definierar då d ( x ) = z + im ( a ). Nu måste man kontrollera att d är väldefinierat (dvs d ( x ) beror bara på x och inte på valet av y ), att det är en homomorfism och att den resulterande långa sekvensen verkligen är exakt. Man kan rutinmässigt verifiera exaktheten genom att diagramjaga (se beviset för Lemma 9.1 i ).

När det är gjort är satsen bevisad för abelska grupper eller moduler över en ring. För det allmänna fallet kan argumentet omformuleras i termer av egenskaper för pilar och annullering istället för element. Alternativt kan man åberopa Mitchells inbäddningssats .

Naturlighet

I applikationerna behöver man ofta visa att långa exakta sekvenser är "naturliga" (i betydelsen naturliga transformationer ). Detta följer av naturligheten i den sekvens som produceras av ormlemma.

Om

är ett kommutativt diagram med exakta rader, då kan ormlemmat appliceras två gånger, på "framsidan" och på "baksidan", vilket ger två långa exakta sekvenser; dessa sammanhänger med ett kommutativt diagram av formen

Exempel

Låt $k$ vara fält, $V$ vara ett $k$ -vektorutrymme. $V$ är $k[t]$ -modul med $t:V\to V$ är en $k$ -linjär transformation, så vi kan tensor $V$ och $k$ över $k[t]$ .

$V\otimes _{k[t]}k=V\otimes _{k[t]}(k[t]/(t))=V/tV=\operatörsnamn {coker} (t).$

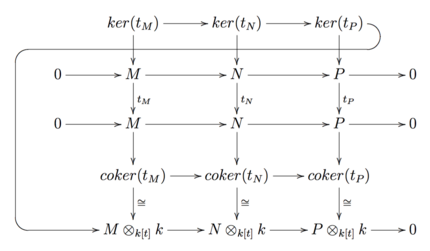
Givet en kort exakt sekvens av $k$ -vektorrum $0\to M\to N\to P\to 0$ , kan vi inducera en exakt sekvens $M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P \otimes _{k[t]}k\to 0$ med rätt exakthet hos tensorprodukten. Men sekvensen $0\to M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0$ är inte exakt i allmänhet. Därför uppstår en naturlig fråga. Varför är denna sekvens inte exakt?

Enligt diagrammet ovan kan vi inducera en exakt sekvens $\ker(t_{M})\to \ker(t_{N})\to \ker(t_{P})\to M\otimes _{k[t]} k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0$ genom att applicera ormlemmat. Således speglar ormlemmat tensorproduktens misslyckande att vara exakt.

I kategorin grupper

Medan många resultat av homologisk algebra, såsom de fem lemma eller de nio lemma , gäller för abelska kategorier såväl som i kategorin grupper, gör inte ormlemmat det. I själva verket existerar inte godtyckliga kokkärnor. Däremot kan man ersätta cokernels med (vänster) coset $A'/\operatorname {im} a$ , $B'/\operatorname {im} b$ , och $C'/\operatörsnamn {im} c$ . Då kan den sammanbindande homomorfismen fortfarande definieras, och man kan skriva ner en sekvens som i uttalandet av ormlemmat. Detta kommer alltid att vara ett kedjekomplex, men det kanske inte är exakt. Exakthet kan dock hävdas när de vertikala sekvenserna i diagrammet är exakta, det vill säga när bilderna av a , b , och c är normala undergrupper .

Motexempel

Betrakta den alternerande gruppen $A_{5}$ : denna innehåller en undergrupp som är isomorf till den symmetriska gruppen ${\displaystyle S_{3}} ,$ som i sin tur kan skrivas som en halvdirekt produkt av cykliska grupper : $S_{3}\simeq C_{3}\rtider C_{2}$ . Detta ger upphov till följande diagram med exakta rader:

${\begin{matrix}&1&\to &C_{3}&\to &C_{3}&\to 1\\ &\downarrow &&\downarrow &&\downarrow \\1\to &1&\to &S_{3}&\to &A_{5}\end{matris}}$

Observera att mittkolumnen inte är exakt: $C_{2}$ är inte en normal undergrupp i halvdirektprodukten.

Eftersom $A_{5}$ är enkel , har den högra vertikala pilen en trivial cokernel. Samtidigt är kvotgruppen $S_{3}/C_{3}$ isomorf till $C_{2}$ . Sekvensen i uttalandet av ormlemma är därför

$1\longrightarrow 1\longrightarrow 1\longrightarrow 1\longrightarrow C_{2}\longrightarrow 1$ ,

vilket verkligen inte är exakt.

I populärkulturen

Beviset på ormlemmat lärs ut av Jill Clayburghs karaktär i början av 1980-filmen It's My Turn .

Se även

• Sicksack-lemma

•   Lang, Serge (2002). "III §9 Ormlemma" . Algebra (3:e uppl.). Springer. s. 157–9. ISBN 978-0-387-95385-4 .
•   Atiyah, MF ; Macdonald, IG (1969). Introduktion till kommutativ algebra . Addison-Wesley. ISBN 0-201-00361-9 .
•   Hilton, P.; Stammbach, U. (1997). En kurs i homologisk algebra . Graduate Texts in Mathematics . Springer. sid. 99. ISBN 0-387-94823-6 .

externa länkar

• Weisstein, Eric W. "Snake Lemma" . MathWorld .
• Snake Lemma på PlanetMath
• Proof of the Snake Lemma i filmen It's My Turn