Nio lemma

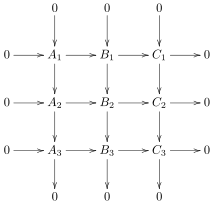
Inom matematik är nio -lemmat (eller 3×3-lemmat) ett påstående om kommutativa diagram och exakta sekvenser som är giltiga i kategorin grupper och alla abelska kategorier . Det står: om diagrammet till höger är ett kommutativt diagram och alla kolumner såväl som de två nedersta raderna är exakta, så är den översta raden också exakt. På samma sätt, om alla kolumner såväl som de två översta raderna är exakta, är den nedre raden också exakt. På samma sätt, eftersom diagrammet är symmetriskt om dess diagonal, kan rader och kolumner bytas ut i ovanstående.

De nio lemmat kan bevisas genom direkt diagramchasing , eller genom att applicera ormlemmat (på de två nedre raderna i det första fallet och på de två översta raderna i det andra fallet).

Linderholm (s. 201) ger en satirisk bild av de nio lemma:

"Rita en noll-och-kors- tavla... Fyll inte i den med nollar och kryss... Använd istället böjda pilar... Vifta med händerna i komplicerade mönster över den här tavlan. Gör några nollor, men inte i rutorna; sätt dem i båda ändarna av de horisontella och vertikala linjerna. Gör ansikten. Du har nu bevisat:

(a) de nio lemma

(b) de sexton lemma

(c) de tjugofem lemma..."

Det finns två varianter av nio lemma: skarpa nio lemma och symmetriska nio lemma (se lemman 3.3, 3.4 i kapitel XII av ).

•   Linderholm, Carl (1971). Matematik gjorde det svårt . Wolfe. ISBN 0-7234-0415-1 .