Slerp

Inom datorgrafik är Slerp en förkortning för sfärisk linjär interpolation , introducerad av Ken Shoemake i samband med quaternion interpolation i syfte att animera 3D - rotation . Det hänvisar till konstant hastighetsrörelse längs en storcirkelbåge med enhetsradie, givet ändarna och en interpolationsparameter mellan 0 och 1.

Geometrisk Slerp

₀ Slerp har en geometrisk formel oberoende av kvaternioner, och oberoende av dimensionen på det utrymme där bågen är inbäddad. Denna formel, en symmetrisk viktad summa som krediteras Glenn Davis, är baserad på det faktum att varje punkt på kurvan måste vara en linjär kombination av ändarna. Låt p och p ₁ vara de första och sista punkterna i bågen, och låt t vara parametern, 0 ≤ t ≤ 1. Beräkna Ω som vinkeln under bågen, så att ₀ cos Ω = p ∙ p ₁ , den n -dimensionell punktprodukt av enhetsvektorerna från ursprunget till ändarna. Den geometriska formeln är då

\operatorname {Slerp} (p_{0},p_{1};t)={\frac {\sin {[(1-t)\Omega }]}{\sin \Omega }}p_{0 }+{\frac {\sin[t\Omega ]}{\sin \Omega }}p_{1}.

Symmetrin ligger i att $\operatorname {Slerp} (p_{0},p_{1};t)$ $=\operatörsnamn {Slerp} (p_{1},p_{0};1-t)$ . I gränsen som Ω → 0, reduceras denna formel till motsvarande symmetriska formel för linjär interpolation ,

\operatorname {Lerp} (p_{0},p_{1};t)=(1-t)p_{0}+tp_{1}.\,\!

En Slerp-bana är i själva verket den sfäriska geometriska ekvivalenten av en bana längs ett linjesegment i planet; en storcirkel är en sfärisk geodetik .

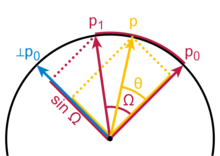
Snedvektor korrigerar till Slerp-faktor.

₀₀ Mer bekant än den allmänna Slerp-formeln är fallet när ändvektorerna är vinkelräta, i vilket fall formeln är ₀ p cos θ + p ₁ sin θ . Om man låter θ = t $π$ /2 , och tillämpar den trigonometriska identiteten cos θ = sin ( $π$ /2 − θ ) , blir detta Slerp-formeln. Faktorn 1/sin Ω i den allmänna formeln är en normalisering, eftersom en vektor p ₁ i en vinkel av Ω till p projicerar ut på vinkelrät ⊥ p med en längd av endast sin Ω .

₀ Vissa speciella fall av Slerp medger mer effektiv beräkning. När en cirkelbåge ska ritas in i en rasterbild är den föredragna metoden någon variant av Bresenhams cirkelalgoritm . Utvärdering vid de speciella parametervärdena 0 och 1 ger trivialt p och p ₁ ; och halvering, utvärdering vid ½, förenklas till ₀ ( p + p ₁ )/2 , normaliserad. Ett annat specialfall, vanligt inom animering, är utvärdering med fasta ändar och lika parametriska steg. Om p _{k −1} och p _k är två på varandra följande värden, och om c är två gånger deras punktprodukt (konstant för alla steg), så är nästa värde, p _{k +1} , reflektionen p _{k +1} = c p _k − pk _{− 1} .

Quaternion Slerp

När Slerp tillämpas på enhetskvaternioner , mappas quaternionbanan till en bana genom 3D-rotationer på ett standardsätt . Effekten är en rotation med enhetlig vinkelhastighet runt en fast rotationsaxel . När den initiala slutpunkten är identitetskvarternionen, ger Slerp ett segment av en enparameters undergrupp av både Lie-gruppen av 3D-rotationer, SO(3) , och dess universella täckande grupp av enhetskvaternioner, S ³ . Slerp ger en rakaste och kortaste vägen mellan dess ändpunkter för kvaternion och mappar till en rotation genom en vinkel på 2Ω. Men eftersom täckningen är dubbel ( q och − q avbildar till samma rotation), kan rotationsvägen vända antingen den "korta vägen" (mindre än 180°) eller den "långa vägen" (mer än 180°). Långa banor kan förhindras genom att negera ena änden om punktprodukten, cos Ω , är negativ, vilket säkerställer att −90° ≤ Ω ≤ 90°.

Slerp har också uttryck i termer av kvaternionalgebra, alla med hjälp av exponentiering . Verkliga potenser av en kvartjon definieras i termer av den exponentiella kvaternionfunktionen , skriven som e ^q och ges av potensserien som är lika bekant från kalkyl, komplex analys och matrisalgebra:

e^{q}=1+q+{\frac {q^{2}}{2}}+{\frac {q^{3}}{6}}+\cdots +{\frac {q ^{n}}{n!}}+\cdots .

Om vi skriver en enhet quaternion q i versorform , cos Ω + v sin Ω , med v en enhet 3-vektor, och noterar att quaternion square v ² är lika med −1 (vilket innebär en quaternion version av Eulers formel ), har vi e ^{v Ω} = q , och q ^t = cos t Ω + v sin t Ω . Identifieringen av intresse är ₀ q = q ₁ q ⁻¹ , så att den reella delen av q är cos Ω , samma som den geometriska punktprodukten som används ovan. Här är fyra ekvivalenta quaternion-uttryck för Slerp.

{\begin{aligned}\operatörsnamn {Slerp} (q_{0},q_{1},t)&=q_{0}(q_{0}^{-1}q_ {1})^{t}\\[6pt]&=q_{1}(q_{1}^{-1}q_{0})^{1-t}\\[6pt]&=(q_{ 0}q_{1}^{-1})^{1-t}q_{1}\\[6pt]&=(q_{1}q_{0}^{-1})^{t}q_{ 0}\end{aligned}}

₀ Derivatan av ₀ Slerp( q , q ₁ ; t ) med avseende på t , förutsatt att ändarna är fixerade, är log( ^{q 1 q −1} ) _gånger funktionsvärdet , där den naturliga kvartjonens logaritmen i detta fall ger hälften av 3D- vinkeln hastighet vektor. Den initiala tangentvektorn transporteras parallellt till varje tangent längs kurvan; sålunda är kurvan verkligen en geodetisk.

I tangentrymden vid valfri punkt på en quaternion Slerp-kurva, omvandlar inversen av exponentialkartan kurvan till ett linjesegment. Slerp-kurvor som inte sträcker sig genom en punkt kan inte omvandlas till linjer i den punktens tangentrymd.

Quaternion Slerps används vanligtvis för att konstruera jämna animationskurvor genom att efterlikna affina konstruktioner som de Casteljau-algoritmen för Bézier-kurvor . Eftersom sfären inte är ett affint utrymme , kan bekanta egenskaper hos affina konstruktioner misslyckas, även om de konstruerade kurvorna annars kan vara helt tillfredsställande. Till exempel kan de Casteljau-algoritmen användas för att dela en kurva i affint utrymme; detta fungerar inte på en sfär.

Den tvåvärdiga Slerp kan utökas för att interpolera bland många enhetskvaternioner, men förlängningen förlorar den fasta exekveringstiden för Slerp-algoritmen.

Se även

externa länkar

Skomakare, Ken. "Animera rotation med Quaternion-kurvor" (PDF) . SIGGRAPH 1985. {{ citera webben }} : CS1 underhåll: url-status ( länk )
Erik B., Dam; Martin, Koch; Lillholm, Martin (17 juli 1998). "Quaternions, Interpolation and Animation" (PDF) . Köpenhamns universitet. Arkiverad (PDF) från originalet 2017-08-30.
Blow, Jonathan (26 februari 2004). "Förstå Slerp, sedan inte använda det" . Arkiverad från originalet 2017-08-25.
Martin, Brian (23 juni 1999). "Brian Martin på Quaternion Animation" . Arkiverad från originalet 2016-03-24.