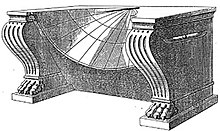
Scafe
Scaphe ( antikgrekiska : σκάφη , romaniserad : scaphe , lit. 'skål'; även känd som en skaphe, scaphion (diminutiv) eller latin : scaphium ) var ett solur som sades ha uppfunnits av Aristarchus från Samos (300-talet f.Kr.) . Det finns inga originalverk som fortfarande finns kvar av Aristarchus, men den intilliggande bilden är en bild av hur den kan ha sett ut; bara hans skulle ha varit gjord av sten. Den bestod av en halvklotformad skål som hade en vertikal gnomon placerad inuti den, med toppen av gnomon i nivå med skålens kant. Tolv graderingar inskrivna vinkelrätt mot halvklotet indikerade tiden på dygnet.
Uppfinnare
Aristarchus från Samos ( / ˌ æ r ə ˈ s t ɑːr k ə s / ; Ἀρίσταρχος , Aristarkhos ; c. 310 – c. 230 f.Kr.) var en forntida grekisk modell som presenterade den första soltematiska astronomen och matematikern som presenterade den första Sunthematicianer och matte. mitten av det kända universum med jorden som kretsar runt det (se Solsystemet ) . Han var influerad av Philolaus av Croton , men han identifierade "den centrala elden" med solen och satte de andra planeterna i deras korrekta avståndsordning runt solen. Hans astronomiska idéer förkastades ofta till förmån för Aristoteles och Ptolemaios geocentriska teorier .
Historia
Greker och romare använde stora solur av sten baserade på "en partiell sfär eller scafe", skuggan av spetsen på gnomonen var det tidtalande indexet. Dessa urtavlor kunde i teorin tala om tiden exakt om de ristades till en sann sfär och korrekt kalibrerade för en given webbplats.
Det tog en skicklig stenarbetare och mycket tid och pengar att skapa ett solur. Så bara förmögna medborgare hade råd med denna komplicerade utrustning, och det var ofta för sina villor eller som donationer för uppförande i stadens forum. Det fanns ett behov av billigare urtavlor som vanliga arbetare kunde konstruera. Men även om det var enklare att göra, var frågan om att kalibrera skalet fortfarande ett problem.
Problemet med att projicera den tredimensionella scafe-urtavlan på ett vertikalt eller horisontellt plan togs upp av ett antal framstående 1800-talsmatematiker, som var och en förmodligen löste det till sin egen personliga belåtenhet. Tyvärr är deras publikationer så komplexa, långrandiga och oklara att de var praktiskt taget otillgängliga för antikvarier och – det skulle framgå av replikeringen av ansträngningar – till och med för deras egna (oerkända) kollegor. Den sfäriska trigonometrin som krävs för den senare strävan är egentligen ganska grundläggande, och beräkningarna tråkiga snarare än svåra. Tillgången till datorgenererad grafik har naturligtvis helt förändrat situationen. Ett Fortran- program skrevs för VAX -datorn vid University of Leicester som gjorde det möjligt att rita vertikala eller horisontella rattar för vilken latitud som helst.
Se även
Bibliografi
- Biémont, E., "Time Measurement in Astronomy" i Heck, A. (red.) (2003), Information Handling in Astronomy: Historical Vistas , sidan 20. Springer.
- Makowski, Georgej, Strong, Williamr. "Sizing Up Earth: En universell metod för att tillämpa Eratosthenes jordmätning." Journal of Geography , 1996, vol. 95, nr 4, sid. 174-179.
- Mills, Allan A. "Solur för säsongens timmar på vertikala och horisontella plan, med en förklaring av scratch-urtavlan." Annals of Science , 1993, vol. 50, nr 1, sid. 83-93.
- Resnikoff, H. och R. O'Neil Wells. (1984), Mathematics in Civilization , sidorna 93–93. Courier Dover Publikationer.
externa länkar
-
 Media relaterade till skålformade solur på Wikimedia Commons
Media relaterade till skålformade solur på Wikimedia Commons