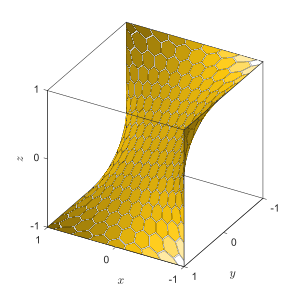
Apsadel

I matematik är apsadeln den yta som definieras av ekvationen

$z=x^{3}-3xy^{2},\,$

eller i cylindriska koordinater

$z=\rho ^{3}\cos(3\varphi ).$

Apsadeln

Den tillhör klassen av sadelytor , och dess namn kommer från observationen att en sadel för en apa skulle kräva två fördjupningar för benen och en för svansen. Punkten $(0,0,0)$ på apsadeln motsvarar en degenererad kritisk punkt för funktionen $z(x,y)$ vid $(0,0)$ . Apsadeln har en isolerad navelpunkt med noll Gaussisk krökning vid utgången, medan krökningen är strikt negativ vid alla andra punkter.

Man kan relatera de rektangulära och cylindriska ekvationerna med hjälp av komplexa tal $x+iy=re^{i\varphi }:$

$z=x^{3}-3xy^{2}=\operatörsnamn {Re} [(x+iy)^{3}]=\operatörsnamn {Re} [r^{3}e^{3i\ varphi }]=r^{3}\cos(3\varphi ).$

Genom att ersätta 3 i den cylindriska ekvationen med valfritt heltal $k\geq 1,$ kan man skapa en sadel med $k$ fördjupningar.

En annan orientering av apsadeln är Smelt-kronbladen definierad av $x+y+z+xyz=0,$ så att apsadelns z- axel motsvarar riktning $(1,1,1)$ i Smelt-kronbladet.

Smält kronblad: x + y + z + xyz = 0

Hästsadel

Termen hästsadel kan användas i motsats till apsadel, för att beteckna en vanlig sadelyta där z ( x , y ) har en sadelpunkt , ett lokalt minimum eller maximum i varje riktning av xy -planet. Däremot har apsadeln en stationär böjningspunkt i alla riktningar.

externa länkar

• Weisstein, Eric W. "Monkey Saddle" . MathWorld .