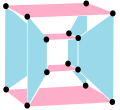
Regelbunden komplex polygon

Tre vyer av vanlig komplex polygon ₄ {4} ₂ ,

Denna komplexa polygon har 8 kanter (komplexa linjer), märkta som en .. h , och 16 hörn. Fyra hörn ligger i varje kant och två kanter skär varandra vid varje vertex. I den vänstra bilden är de konturerade kvadraterna inte element i polytopen utan ingår bara för att hjälpa till att identifiera hörn som ligger i samma komplexa linje. Den åttakantiga omkretsen av den vänstra bilden är inte ett element i polytopen, utan det är en petriepolygon . I mittenbilden är varje kant representerad som en riktig linje och de fyra hörnen i varje linje kan ses tydligare.

En perspektivskiss som representerar de 16 vertexpunkterna som stora svarta prickar och de 8 4-kanterna som avgränsade rutor inom varje kant. Den gröna banan representerar den åttakantiga omkretsen av den vänstra bilden.

Komplexa 1-polytoper representerade i Argand-planet som regelbundna polygoner för p = 2, 3, 4, 5 och 6, med svarta hörn. Centroiden för p -hörnen visas i rött. Sidorna på polygonerna representerar en tillämpning av symmetrigeneratorn, som mappar varje vertex till nästa moturs kopia. Dessa polygonala sidor är inte kantelement av polytopen, eftersom en komplex 1-polytop inte kan ha några kanter (det är ofta en komplex kant) och bara innehåller vertexelement.

Inom geometri är en regelbunden komplex polygon en generalisering av en regelbunden polygon i verkliga rymden till en analog struktur i ett komplext Hilbert-rum , där varje verklig dimension åtföljs av en imaginär . En vanlig polygon finns i två reella dimensioner, $\mathbb {R} ^{2}$ , medan en komplex polygon finns i två komplexa dimensioner, $\mathbb {C} ^{2}$ , som kan ges reella representationer i 4 dimensioner, ${\displaystyle \mathbb {R} ^{4}} ,$ som sedan måste projiceras ner till 2 eller 3 reella dimensioner för att kunna visualiseras. En komplex polygon generaliseras som en komplex polytop i $\mathbb {C} ^{n}$ .

En komplex polygon kan förstås som en samling av komplexa punkter, linjer, plan och så vidare, där varje punkt är korsningen mellan flera linjer, varje linje med flera plan, och så vidare.

De vanliga komplexa polygonerna har karakteriserats fullständigt och kan beskrivas med en symbolisk notation utvecklad av Coxeter .

Regelbundna komplexa polygoner

Medan 1-polytoper kan ha obegränsat p , är ändliga reguljära komplexa polygoner, exklusive de dubbla prismapolygonerna _p {4} ₂ , begränsade till element med 5-kanter (pentagonala kanter), och oändliga regelbundna aperigoner inkluderar även 6-kanter (hexagonala kanter) element.

Noteringar

Shephards modifierade Schläfli-notation

Shephard utarbetade ursprungligen en modifierad form av Schläflis notation för vanliga polytoper. För en polygon som avgränsas av p ₁ -kanter, med en p ₂ -uppsättning som vertexfigur och en övergripande symmetrigrupp av ordningen g , betecknar vi polygonen som p ₁ ( g ) p ₂ .

Antalet hörn V är då g / p ₂ och antalet kanter E är g / p ₁ .

Den komplexa polygonen som illustreras ovan har åtta kvadratiska kanter ( p ₁ =4) och sexton hörn ( p ₂ = 2). Utifrån detta kan vi räkna ut att g = 32, vilket ger den modifierade Schläfli-symbolen 4(32)2.

Coxeters reviderade modifierade Schläfli-notation

En modernare notation _{p 1} { q } _{p 2} beror på Coxeter , och är baserad på gruppteori. Som en symmetrigrupp är dess symbol _{p 1} [ q ] _{p 2} .

Symmetrigruppen _{p 1} [ q ] _{p 2} representeras av 2 generatorer R ₁ , R ₂ , där: R ₁ ^{p ₁} = R ₂ ^{p ₂} = I. Om q är jämn, (R ₂ R ₁ ) ^{q /2} = ( _{RiR2 )} q / ^{2 .} _ Om q är udda, (R _2R 1 ) ^{( q −1)/2} R 2 ₌ (R ₁ R ₂ ) ^{( q −1)/2} R _{1 .} När q är udda, är p ₁ = p ₂ .

För ₄ [ 4 _{] 2} har _R14 = _R22 = I , ⁽ _R2R1 ) ² = ⁽ _R1R2 ⁾ 2 _.

För _{3 [} 5 _{] 3} har _R13 = ^R23 ₌ I , ( _R2R1 ) ^2R2 = ⁽ R1R2 ₎ 2R1 _. ^_ _ _{_} _

Coxeter–Dynkin-diagram

Coxeter generaliserade också användningen av Coxeter-Dynkin-diagram till komplexa polytoper, till exempel representeras den komplexa polygonen _p { q } _{r av} och den ekvivalenta symmetrigruppen, _p [ q ​​] _r , är ett ringlöst diagram . Noderna p och r representerar speglar som producerar p- och r -bilder i planet. Omärkta noder i ett diagram har implicita 2 etiketter. Till exempel är en riktig vanlig polygon ₂ { q } ₂ eller { q } eller .

En begränsning, noder anslutna med udda grenorder måste ha identiska nodordningar. Om de inte gör det kommer gruppen att skapa "stjärnklara" polygoner med överlappande element. Så och är vanliga, medan är stjärnklara.

12 Irreducible Shephard-grupper

12 irreducerbara Shephard-grupper med deras undergruppsindexrelationer.	Undergrupper från <5,3,2> 30 , <4,3,2> 12 och <3,3,2> 6
Undergrupper relaterar genom att ta bort en reflektion: p [2 q ] 2 --> p [ q ] p , index 2 och p [4] q --> p [ q ] p , index q .

_p [4] ₂ undergrupper: p=2,3,4... _p [4] ₂ --> [ p ], index p _p [4] ₂ --> _p []× _p [], index 2

Coxeter räknade upp denna lista med vanliga komplexa polygoner i $\mathbb {C} ^{2}$ . En vanlig komplex polygon, _p { q } _r eller , har p -kanter och r -gonala vertexfigurer . _p { q } _r är en finit polytop om ( p + r ) q > pr ( q − 2).

Dess symmetri skrivs som _p [ q ] _r , kallad en Shephard-grupp , analogt med en Coxeter-grupp , samtidigt som den tillåter enhetliga reflektioner .

För icke-stjärniga grupper kan ordningen för gruppen _p [ q ] _r beräknas som $g=8/q\ cdot (1/p+2/q+1/r-1)^{-2}$ .

Coxeter -talet för _p [ q ] _r är $h=2/(1/p+2/q+1/r-1 )$ , så gruppordningen kan också beräknas som $g=2h^{2}/q$ . En vanlig komplex polygon kan ritas i ortogonal projektion med h -gonal symmetri.

De två lösningarna som genererar komplexa polygoner är:

Grupp	G 3 = G( q ,1,1)	G 2 = G( p ,1,2)	G 4	G 6	G 5	G 8	G 14	G 9	G 10	G 20	G 16	G 21	G 17	G 18
	2 [ q ] 2 , q = 3,4...	p [4] 2 , p = 2,3...	3 [3] 3	3 [6] 2	3 [4] 3	4 [3] 4	3 [8] 2	4 [6] 2	4 [4] 3	3 [5] 3	5 [3] 5	3 [10] 2	5 [6] 2	5 [4] 3
Beställa	2 q	2 p 2	24	48	72	96	144	192	288	360	600	720	1200	1800
h	q	2 sid	6	12			24			30		60

Undantagna lösningar med udda q och olika p och r är: ₆ [3] ₂ , ₆ [3] ₃ , ₉ [3] ₃ , ₁₂ [3] ₃ , ..., ₅ [5] ₂ , ₆ [5] ₂ , ₈ [5] ₂ , ₉ [5] ₂ , ₄ [7] ₂ , ₉ [5] ₂ , ₃ [9] ₂ och ₃ [11] ₂ .

Andra hela q med ojämna p och r , skapa stjärnklara grupper med överlappande fundamentala domäner: , , , , , och .

Den dubbla polygonen för _p { q } _r är _r { q } _p . En polygon av formen _p { q } _p är självdual. Grupper av formen _p [2 q ] ₂ har en halvsymmetri _p [ q ] _p , så en regelbunden polygon är detsamma som kvasiregular . Dessutom har vanlig polygon med samma nodordningar, , en alternerad konstruktion , vilket gör att intilliggande kanter kan ha två olika färger.

Gruppordningen, g , används för att beräkna det totala antalet hörn och kanter. Den kommer att ha g / r -hörn och g / p -kanter. När p = r är antalet hörn och kanter lika. Detta villkor krävs när q är udda.

Matrisgeneratorer

Gruppen p [ q ] r , , kan representeras av två matriser:

namn	R 1	R 2
Beställa	sid	r
Matris	$\left[{\begin{smallmatrix}e^{2\pi i/p}&0\\(e^{2 \pi i/p}-1)k&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}1&(e^{2\pi i/r}-1)k\\ 0&e^{2\pi i/r}\end{smallmatrix}}\right]$

Med

$k={\sqrt {\frac {\cos({\frac {\pi } {p}}-{\frac {\pi }{r}})+\cos({\frac {2\pi }{q}})}{2\sin {\frac {\pi }{p}} \sin {\frac {\pi }{r}}}}}$

Exempel

namn R 1 R 2 Beställa sid q Matris $\left[{\begin{smallmatrix}e^{2\pi i/p}&0\\0&1\\\end{smallmatrix}}\right]$ $\left[{\begin{smallmatrix}1&0\\0&e^{2\pi i/q}\\\end{smallmatrix}}\right]$	namn R 1 R 2 Beställa sid 2 Matris $\left[{\begin{smallmatrix}e^{2\pi i/p}&0\\0&1\\\end{smallmatrix}}\right]$ $\left[{\begin{smallmatrix}0&1\\1&0\\\end{smallmatrix}}\right]$	namn R 1 R 2 Beställa 3 3 Matris $\left[{\begin{smallmatrix}{\frac {-1+{\sqrt {3}}i}{2}}&0\\ {\frac {-3+{\sqrt {3}}i}{2}}&1\\\end{smallmatrix}}\right]$ $\left[{\begin{smallmatrix}1&{\frac {-3+{\sqrt {3}}i}{2}}\\ 0&{\frac {-1+{\sqrt {3}}i}{2}}\\\end{smallmatrix}}\right]$
namn R 1 R 2 Beställa 4 4 Matris $\left[{\begin{smallmatrix}i&0\\0&1\\\end{smallmatrix}}\right]$ $\left[{\begin{smallmatrix}1&0\\0&i\\\end{smallmatrix}}\right]$	namn R 1 R 2 Beställa 4 2 Matris $\left[{\begin{smallmatrix}i&0\\0&1\\\end{smallmatrix}}\right]$ $\left[{\begin{smallmatrix}0&1\\1&0\\\end{smallmatrix}}\right]$	namn R 1 R 2 Beställa 3 2 Matris $\left[{\begin{smallmatrix}{\frac {-1+{\sqrt {3}}i}{2}}&0\\ {\frac {-3+{\sqrt {3}}i}{2}}&1\\\end{smallmatrix}}\right]$ $\left[{\begin{smallmatrix}1&-2\\0&-1\\\end{smallmatrix}}\right]$

Uppräkning av regelbundna komplexa polygoner

Coxeter räknade upp de komplexa polygonerna i Tabell III av Regular Complex Polytopes.

Grupp	Beställa	Coxeter nummer	Polygon		Vertices	Kanter		Anteckningar
G ( q , q ,2) 2 [ q ] 2 = [ q ] q = 2,3,4,...	2 q	q	2 { q } 2		q	q	{}	Verkliga reguljära polygoner Samma som Samma som om q jämnt

Grupp	Beställa	Coxeter nummer	Polygon			Vertices	Kanter		Anteckningar
G( p ,1,2) p [4] 2 p=2,3,4,...	2 p 2	2 sid	p ( 2p2 ) 2	p {4} 2		p 2	2 sid	p {}	samma som p {}× p {} eller $\mathbb {R} ^{4}$ representation som p - p duoprism
			2(2 p 2 ) sid	2 {4} sid		2 sid	p 2	{}	$\mathbb {R} ^{4}$ representation som p - p duopyramid
G(2,1,2) 2 [4] 2 = [4]	8	4		2 {4} 2 = {4}		4	4	{}	samma som {}×{} eller verklig kvadrat
G(3,1,2) 3 [4] 2	18	6	6(18)2	3 {4} 2		9	6	3 {}	samma som 3 {}× 3 {} eller $\mathbb {R} ^{4}$ representation som 3-3 duoprism
			2(18)3	2 {4} 3		6	9	{}	$\mathbb {R} ^{4}$ representation som 3-3 duopyramid
G(4,1,2) 4 [4] 2	32	8	8(32)2	4 {4} 2		16	8	4 {}	samma som 4 {}× 4 {} eller $\mathbb {R} ^{4}$ representation som 4-4 duoprism eller {4,3,3}
			2(32)4	2 {4} 4		8	16	{}	$\mathbb {R} ^{4}$ representation som 4-4 duopyramid eller {3,3,4}
G(5,1,2) 5 [4] 2	50	25	5(50)2	5 {4} 2		25	10	5 {}	samma som 5 {}× 5 {} eller $\mathbb {R} ^{4}$ representation som 5-5 duoprism
			2(50)5	2 {4} 5		10	25	{}	$\mathbb {R} ^{4}$ representation som 5-5 duopyramid
G(6,1,2) 6 [4] 2	72	36	6(72)2	6 {4} 2		36	12	6 {}	samma som 6 {}× 6 {} eller $\mathbb {R} ^{4}$ representation som 6-6 duoprism
			2(72)6	2 {4} 6		12	36	{}	$\mathbb {R} ^{4}$ representation som 6-6 duopyramid
G4 =G(1,1,2) 3 [3] 3 <2,3,3 >	24	6	3(24)3	3 {3} 3		8	8	3 {}	Möbius–Kantor konfiguration självdubbel, samma som $\mathbb {R} ^{4}$ representation som {3,3,4}
G 6 3 [6] 2	48	12	3(48)2	3 {6} 2		24	16	3 {}	samma som
				3 {3} 2					stjärnklar polygon
			2(48)3	2 {6} 3		16	24	{}
				2 {3} 3					stjärnklar polygon
G 5 3 [4] 3	72	12	3(72)3	3 {4} 3		24	24	3 {}	självdubbel, samma som $\mathbb {R} ^{4}$ representation som {3,4,3}
G 8 4 [3] 4	96	12	4(96)4	4 {3} 4		24	24	4 {}	självdubbel, samma som $\mathbb {R} ^{4}$ representation som {3,4,3}
G 14 3 [8] 2	144	24	3(144)2	3 {8} 2		72	48	3 {}	samma som
				3 {8/3} 2					stjärnklar polygon, samma som
			2(144)3	2 {8} 3		48	72	{}
				2 {8/3} 3					stjärnklar polygon
G 9 4 [6] 2	192	24	4(192)2	4 {6} 2		96	48	4 {}	samma som
			2(192)4	2 {6} 4		48	96	{}
				4 {3} 2		96	48	{}	stjärnklar polygon
				2 {3} 4		48	96	{}	stjärnklar polygon
G 10 4 [4] 3	288	24	4(288)3	4 {4} 3		96	72	4 {}
		12		4 {8/3} 3					stjärnklar polygon
		24	3(288)4	3 {4} 4		72	96	3 {}
		12		3 {8/3} 4					stjärnklar polygon
G 20 3 [5] 3	360	30	3(360)3	3 {5} 3		120	120	3 {}	självdual, samma som $\mathbb {R} ^{4}$ representation som {3,3,5}
				3 {5/2} 3					självdubbel, stjärnklar polygon
G 16 5 [3] 5	600	30	5(600)5	5 {3} 5		120	120	5 {}	självdual, samma som $\mathbb {R} ^{4}$ representation som {3,3,5}
		10		5 {5/2} 5					självdubbel, stjärnklar polygon
G 21 3 [10] 2	720	60	3(720)2	3 {10} 2		360	240	3 {}	samma som
				3 {5} 2					stjärnklar polygon
				3 {10/3} 2					stjärnklar polygon, samma som
				3 {5/2} 2					stjärnklar polygon
			2(720)3	2 {10} 3		240	360	{}
				2 {5} 3					stjärnklar polygon
				2 {10/3} 3					stjärnklar polygon
				2 {5/2} 3					stjärnklar polygon
G 17 5 [6] 2	1200	60	5(1200)2	5 {6} 2		600	240	5 {}	samma som
		20		5 {5} 2					stjärnklar polygon
		20		5 {10/3} 2					stjärnklar polygon
		60		5 {3} 2					stjärnklar polygon
		60	2(1200)5	2 {6} 5		240	600	{}
		20		2 {5} 5					stjärnklar polygon
		20		2 {10/3} 5					stjärnklar polygon
		60		2 {3} 5					stjärnklar polygon
G 18 5 [4] 3	1800	60	5(1800)3	5 {4} 3		600	360	5 {}
		15		5 {10/3} 3					stjärnklar polygon
		30		5 {3} 3					stjärnklar polygon
		30		5 {5/2} 3					stjärnklar polygon
		60	3(1800)5	3 {4} 5		360	600	3 {}
		15		3 {10/3} 5					stjärnklar polygon
		30		3 {3} 5					stjärnklar polygon
		30		3 {5/2} 5					stjärnklar polygon

Visualiseringar av vanliga komplexa polygoner

2D-grafer

Polygoner av formen _p {2 r } _q kan visualiseras med q färguppsättningar av p -kant. Varje p -kant ses som en vanlig polygon, medan det inte finns några ytor.

Komplexa polygoner ₂ { r } _q

Polygoner av formen ₂ {4} _q kallas generaliserade ortoplexer . De delar hörn med 4D q - q duopyramiderna , hörn sammankopplade med 2-kanter.

• 

  ₂ {4} ₂ , , med 4 hörn och 4 kanter

• 

  ₂ {4} ₃ , , med 6 hörn och 9 kanter

• 

  ₂ {4} ₄ , , med 8 hörn och 16 kanter

• 

  ₂ {4} ₅ , , med 10 hörn och 25 kanter

• 

  ₂ {4} ₆ , , med 12 hörn och 36 kanter

• 

  ₂ {4} ₇ , , med 14 hörn och 49 kanter

• 

  ₂ {4} ₈ , , med 16 hörn och 64 kanter

• 

  ₂ {4} ₉ , , med 18 hörn och 81 kanter

• 

  ₂ {4} ₁₀ , , med 20 hörn och 100 kanter

Komplexa polygoner _p {4} ₂

Polygoner av formen _p {4} ₂ kallas generaliserade hyperkuber (kvadrater för polygoner). De delar hörn med 4D p - p duoprismerna , hörn sammankopplade med p-kanter. Vertices är ritade i grönt, och p -kanter ritas i alternativa färger, rött och blått. Perspektivet är något förvrängt för udda dimensioner för att flytta överlappande hörn från mitten.

• 

  ₂ {4} ₂ , eller , med 4 hörn och 4 2-kanter

• 

  ₃ {4} ₂ , eller , med 9 hörn och 6 (triangulära) 3-kanter

• 

  ₄ {4} ₂ , eller , med 16 hörn och 8 (fyrkantiga) 4-kanter

• 

  ₅ {4} ₂ , eller , med 25 hörn och 10 (femkantiga) 5-kanter

• 

  ₆ {4} ₂ , eller , med 36 hörn och 12 (hexagonala) 6-kanter

• 

  ₇ {4} ₂ , eller , med 49 hörn och 14 (heptagonala) 7-kanter

• 

  ₈ {4} ₂ , eller , med 64 hörn och 16 (åttkantiga) 8-kanter

• 

  ₉ {4} ₂ , eller , med 81 hörn och 18 (enneagonala) 9-kanter

• 

  ₁₀ {4} ₂ , eller , med 100 hörn och 20 (dekagonala) 10-kanter

Komplexa polygoner _p { r } ₂

• 

  ₃ {6} ₂ , eller , med 24 hörn i svart och 16 3-kanter färgade i 2 uppsättningar av 3-kanter i rött och blått

• 

  ₃ {8} ₂ , eller , med 72 hörn i svart och 48 3-kanter färgade i 2 uppsättningar av 3-kanter i rött och blått

Komplexa polygoner, _p { r } _sid

Polygoner av formen _p { r } _p har lika många hörn och kanter. De är också självdubbla.

• 

  ₃ {3} ₃ , eller , med 8 hörn i svart och 8 3-kanter färgade i 2 uppsättningar av 3-kanter i rött och blått

• 

  ₃ {4} ₃ , eller , med 24 hörn och 24 3-kanter visas i 3 uppsättningar färger, en uppsättning fylld

• 

  ₄ {3} ₄ , eller , med 24 hörn och 24 4-kanter visas i 4 uppsättningar färger

• 

  ₃ {5} ₃ , eller , med 120 hörn och 120 3-kanter

• 

  ₅ {3} ₅ , eller , med 120 hörn och 120 5-kanter

3D-perspektiv

3D - perspektivprojektioner av komplexa polygoner _p {4} ₂ kan visa punktkantstrukturen för en komplex polygon, medan skalan inte bevaras.

Dualerna ₂ {4} _p : ses genom att lägga till hörn innanför kanterna och lägga till kanter i stället för hörn.

• 

  ₂ {4} ₃ , med 6 hörn, 9 kanter i 3 set

• 

  ₃ {4} ₂ , med 9 hörn, 6 3-kanter i 2 uppsättningar färger som

• 

  ₄ {4} ₂ , med 16 hörn, 8 4-kanter i 2 uppsättningar färger och fyllda fyrkantiga 4-kanter som

• 

  ₅ {4} ₂ , med 25 hörn, 10 5-kanter i 2 uppsättningar färger som

Kvasiregelbundna polygoner

En kvasiregulär polygon är en trunkering av en vanlig polygon. En kvasiregelbunden polygon innehåller alternativa kanter av de vanliga polygonerna och . Den kvasiregelbundna polygonen har p hörn på p-kanterna av den reguljära formen.

Exempel på kvasiregulära polygoner

p [ q ] r	2 [4] 2	3 [4] 2	4 [4] 2	5 [4] 2	6 [4] 2	7 [4] 2	8 [4] 2	3 [3] 3	3 [4] 3
Regelbunden	4 2-kanter	9 3-kanter	16 4-kanter	25 5-kanter	36 6-kanter	49 7-kanter	64 8-kanter
Kvasiregelbunden	= 4+4 2-kanter	6 2-kanter 9 3-kanter	8 2-kanter 16 4-kanter	10 2-kanter 25 5-kanter	12 2-kanter 36 6-kanter	14 2-kanter 49 7-kanter	16 2-kanter 64 8-kanter	=	=
Regelbunden	4 2-kanter	6 2-kanter	8 2-kanter	10 2-kanter	12 2-kanter	14 2-kanter	16 2-kanter

Anteckningar

• Coxeter, HSM och Moser, WOJ; Generatorer och relationer för diskreta grupper (1965), s. 67–80.
•   Coxeter, HSM (1991), Regular Complex Polytopes , Cambridge University Press, ISBN 0-521-39490-2
• Coxeter, HSM och Shephard, GC; Porträtt av en familj av komplexa polytoper, Leonardo Vol 25, No 3/4, (1992), s 239–244,
• Shephard, GC; Regelbundna komplexa polytoper , Proc. London matematik. Soc. Series 3, Vol 2, (1952), s 82–97.
• GC Shephard , JA Todd, Finita enhetliga reflektionsgrupper , Canadian Journal of Mathematics. 6(1954), 274–304 [1]
• Gustav I. Lehrer och Donald E. Taylor, Unitary Reflection Groups , Cambridge University Press 2009