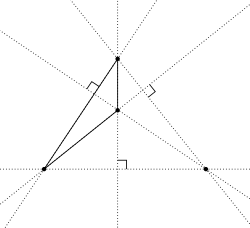
Ortocentriskt system

Ortocentriskt system . Vilken punkt som helst är ortocentrum för triangeln som bildas av de andra tre.

Inom geometri är ett ortocentriskt system en uppsättning av fyra pekar på ett plan , varav en är ortocentrum av triangeln som bildas av de andra tre. På motsvarande sätt är linjerna som går genom osammanhängande par bland punkterna vinkelräta , och de fyra cirklarna som passerar genom tre av de fyra punkterna har samma radie.

Om fyra punkter bildar ett ortocentriskt system, är var och en av de fyra punkterna ortocentrum för de andra tre. Dessa fyra möjliga trianglar kommer alla att ha samma niopunktscirkel . Följaktligen måste dessa fyra möjliga trianglar alla ha circumcircles med samma circumradius .

Den gemensamma niopunktscirkeln

Vanlig niopunktscirkel , där

O, O 4, A 4

är niopunktscentrum, circumcenter respektive ortocenter av triangeln som bildas av de andra tre ortocentriska punkterna

A 1, A 2, A 3

.

Mitten av denna vanliga niopunktscirkel ligger vid tyngdpunkten för de fyra ortocentriska punkterna. Radien för den gemensamma niopunktscirkeln är avståndet från niopunktscentrumet till mittpunkten av någon av de sex kopplingarna som förenar ett par ortocentriska punkter genom vilka den gemensamma niopunktscirkeln passerar. Niopunktscirkeln passerar också genom de tre ortogonala skärningspunkterna vid foten av de fyra möjliga trianglarnas höjder.

Detta vanliga niopunktscentrum ligger vid mittpunkten av kontaktdonet som förenar vilken ortocentrisk punkt som helst med omkretsen av triangeln som bildas av de andra tre ortocentriska punkterna.

Den gemensamma niopunktscirkeln tangerar alla 16 cirklar och cirklar av de fyra trianglarna vars hörn bildar det ortocentriska systemet.

Den vanliga ortiska triangeln, dess incenter och dess excenter

Om de sex kopplingarna som förenar ett par ortocentriska punkter förlängs till sex linjer som skär varandra, genererar de sju skärningspunkter. Fyra av dessa punkter är de ursprungliga ortocentriska punkterna och de ytterligare tre punkterna är de ortogonala skärningspunkterna vid foten av höjderna . Sammanfogningen av dessa tre ortogonala punkter till en triangel genererar en orthostisk triangel som är gemensam för alla de fyra möjliga trianglarna som bildas av de fyra ortocentriska punkterna tagna tre åt gången.

Mitten av denna gemensamma ortos triangel måste vara en av de ursprungliga fyra ortocentriska punkterna . Dessutom blir de tre återstående punkterna excenterna för denna vanliga ortiska triangel. Den ortocentriska punkten som blir mitten av den ortocentriska triangeln är den ortocentriska punkten närmast det vanliga niopunktscentrumet. Detta förhållande mellan den ortocentriska triangeln och de ursprungliga fyra ortocentriska punkterna leder direkt till det faktum att en referenstriangels incenter och excenter bildar ett ortocentriskt system.

Det är normalt att särskilja en av de ortocentriska punkterna från de andra, närmare bestämt den som är mitten av den orthic triangel; denna betecknas $H$ som ortocentrum för de tre yttre ortocentriska punkterna som är valda som referenstriangel $△ ABC$ . I denna normaliserade konfiguration kommer punkten $H$ alltid att ligga inom triangeln $△ ABC$ , och alla vinklar i triangeln $△ ABC$ kommer att vara spetsiga. De fyra möjliga trianglarna som refereras till ovan är då trianglarna $△ ABC, △ ABH, △ ACH, △ BCH$ . De sex anslutningarna ovan är $AB, AC, BC, AH, BH, CH$ . De sju skärningspunkterna som hänvisas till ovan är $A, B, C, H$ (de ursprungliga ortocentriska punkterna) och $H A, H B, H C$ (fötterna på triangeln $△ ABCs höjder$ och den ortosiska triangelns hörn).

Det ortocentriska systemet och dess ortosaxlar

Den ortiska axeln som är associerad med ett normaliserat ortocentriskt system $A, B, C, H$ , där $△ ABC$ är referenstriangeln, är en linje som passerar genom tre skärningspunkter som bildas när varje sida av den ortiska triangeln möter varje sida av referenstriangeln. Betrakta nu de tre andra möjliga trianglarna, $△ ABH, △ ACH, △ BCH$ . De har var sin ortiska axel.

Euler-linjer och homotetiska ortocentriska system

Ortocentriskt system . Där

O 1, O 2, O 3, O 4

är omkretsen av de fyra möjliga trianglarna som bildas av de ortocentriska punkterna

A 1, A 2, A 3, A 4

.

Låt vektorerna $a, b, c, h$ bestämma positionen för var och en av de fyra ortocentriska punkterna och låt $n = (a + b + c + h) / 4$ vara positionsvektorn för $N$ , det gemensamma niopunktscentrumet. Förena var och en av de fyra ortocentriska punkterna till deras gemensamma niopunktscentrum och förläng dem till fyra linjer. Dessa fyra linjer representerar nu Eulerlinjerna för de fyra möjliga trianglarna där den förlängda linjen $HN$ är Eulerlinjen för triangeln $△ ABC$ och den förlängda linjen $AN$ är Eulerlinjen med triangeln $△ BCH$ etc. Om en punkt $P$ väljs på Eulern linje $HN$ i referenstriangeln $△ ABC$ med en positionsvektor $p$ så att $p = n + α(h - n)$ där $α$ är en ren konstant oberoende av placeringen av de fyra ortocentriska punkterna och ytterligare tre punkter $P A, P B, P C$ så att $p a = n + α(a - n)$ etc., då bildar $P, P A, P B, P C ett ortocentriskt system.$ Detta genererade ortocentriska system är alltid homotetiskt till det ursprungliga systemet med fyra punkter med det gemensamma niopunktscentrumet som det homotetiska centret och α förhållandet mellan likhet .

När $P$ väljs som tyngdpunkten $G$ , då är $α = -⅓$ . När $P$ väljs som omkretscentrum $O$ , då är $α = -1$ och det genererade ortocentriska systemet är kongruent med det ursprungliga systemet och är en reflektion av det kring niopunktscentrumet. I denna konfiguration bildar $P A, P B, PC en$ Johnson-triangel av den ursprungliga referenstriangeln $△ ABC$ . Följaktligen är de omslutna cirklarna för de fyra trianglarna $△ ABC, △ ABH, △ ACH, △ BCH$ alla lika och bildar en uppsättning Johnson-cirklar som visas i diagrammet intill.

Ytterligare fastigheter

De fyra Euler-linjerna i ett ortocentriskt system är ortogonala mot de fyra ortocentriska axlarna i ett ortocentriskt system.

De sex kopplingarna som förenar något par av de ursprungliga fyra ortocentriska punkterna kommer att producera par av kopplingar som är ortogonala mot varandra så att de uppfyller avståndsekvationerna

{\ overline {CH}}^{2}={\overline {AC}}^{2}+{\overline {BH}}^{2}={\overline {BC}}^{2}+{\overline { AH}}^{2}=4R^{2}}

där $R$ är den gemensamma omkretsradien för de fyra möjliga trianglarna. Dessa ekvationer tillsammans med sinuslagen resulterar i identiteten

{\frac {\overline {BC}}{\sin A}}={\frac {\overline {AC}}{\sin B}}={\frac {\overline {AB}}{\sin C}}={\frac {\overline {HA}}{|\cos A|}}={\frac {\overline {HB}}{|\cos B|}}={\frac {\overline {HC }}{|\cos C|}}=2R.

Feuerbachs teorem säger att niopunktscirkeln tangerar incirkeln och de tre excirklarna i en referenstriangel. Eftersom niopunktscirkeln är gemensam för alla fyra möjliga trianglar i ett ortocentriskt system, tangerar den 16 cirklar som består av de fyra möjliga trianglarnas incirklar och excirklar.

Varje kon som passerar genom de fyra ortocentriska punkterna kan bara vara en rektangulär hyperbel . Detta är ett resultat av Feuerbachs koniska teorem som säger att för alla circumconics i en referenstriangel som också passerar genom dess ortocenter, bildar platsen för centrum för sådana circumconics niopunktscirkeln och att circumconics endast kan vara rektangulära hyperboler. Platsen för perspektörerna i denna familj av rektangulära hyperboler kommer alltid att ligga på de fyra ortiska axlarna. Så om en rektangulär hyperbel dras genom fyra ortocentriska punkter kommer den att ha ett fast centrum på den gemensamma niopunktscirkeln, men den kommer att ha fyra perspektivbilder en på var och en av de fyra möjliga trianglarnas ortiska axlar. Den ena punkten på niopunktscirkeln som är centrum för denna rektangulära hyperbel kommer att ha fyra olika definitioner beroende på vilken av de fyra möjliga trianglarna som används som referenstriangel.

De väldokumenterade rektangulära hyperbolerna som passerar genom fyra ortocentriska punkter är Feuerbach-, Jeřábek- och Kiepert-cirkumhyperbolerna i referenstriangeln $△ ABC$ i ett normaliserat system med $H$ som ortocentrum.

De fyra möjliga trianglarna har en uppsättning av fyra inkoner som kallas ortiska inkoner som delar vissa egenskaper. Kontakterna för dessa inkoner med de fyra möjliga trianglarna uppstår vid hörnen av deras gemensamma ortiska triangel. I ett normaliserat ortocentriskt system är den orthic inconic som tangerar sidorna av triangeln △ $ABC en$ inellips och de orthic inconics av de andra tre möjliga trianglarna är hyperboler. Dessa fyra orthic inconics delar också samma Brianchon- punkt $H$ , den ortocentriska punkten närmast det gemensamma niopunktscentrumet. Centrum för dessa orthic inconics är symmedianpunkterna $K$ för de fyra möjliga trianglarna.

Det finns många dokumenterade kubik som passerar genom en referenstriangel och dess ortocenter. Den cirkumkubiska känd som ortokubiken - K006 är intressant genom att den passerar genom tre ortocentriska system såväl som de tre hörnen av den orthic triangeln (men inte ortocentret av den orthic triangeln). De tre ortocentriska systemen är incenter och excenter, referenstriangeln och dess ortocenter och slutligen ortocentrum för referenstriangeln tillsammans med de tre andra skärningspunkterna som denna kub har med referenstriangelns omkretscirkel.

Alla två polära cirklar av två trianglar i ett ortocentriskt system är ortogonala .

Anteckningar

Johnson, Roger A. (1929). Modern Geometry: En elementär avhandling om triangelns och cirkelns geometri . Houghton Mifflin. Återpublicerad som Advanced Euclidean Geometry . Dover. 1960; 2007. Se särskilt kapitel IX. Tre anmärkningsvärda punkter .

externa länkar

Weisstein, Eric W. "Orthocenter" . MathWorld .
Weisstein, Eric W. "Feuerbachs sats" . MathWorld .
Weisstein, Eric W. "Feuerbachs koniska sats" . MathWorld .
Weisstein, Eric W. "Feuerbach Hyperbola" . MathWorld .
Weisstein, Eric W. "Jerabek Hyperbola" . MathWorld .
Weisstein, Eric W. "Kiepert Hyperbola" . MathWorld .
Weisstein, Eric W. "Orthic Inconic" . MathWorld .
Weisstein, Eric W. "Orthic Axis" . MathWorld .
Weisstein, Eric W. "Perspector" . MathWorld .
Bernard Gibert Circumcubic K006
Clark Kimberling, " Encyclopedia of triangle centers ". (Listar cirka 5000 intressanta punkter som är associerade med valfri triangel.)