Johnson cirklar

J A ≅ J B ≅ J C

med radien

r

(skär varandra vid

H

; par skär varandra vid

A, B, C

)

Cirkel som går genom

A, B, C

(har radien

r

enligt Johnsons sats)

Johnson triangel

△ J A J B J C

av

△ ABC

Omkrets av

△ J A J B J C

(radie

r

)

Inom geometri består en uppsättning Johnson-cirklar av tre cirklar med samma radie r $som$ delar en gemensam skärningspunkt $H.$ I en sådan konfiguration har cirklarna vanligtvis totalt fyra skärningspunkter (punkter där minst två av dem möts): den gemensamma punkten $H$ som de alla delar, och för vart och ett av de tre paren av cirklar ytterligare en skärningspunkt (här kallad deras 2-visa skärningspunkt). Om två av cirklarna råkar oskulera har de bara $H$ som en gemensam punkt, och det kommer då att anses att $H$ också är deras 2-visa skärningspunkt; om de skulle sammanfalla förklarar vi att deras 2-visa skärningspunkt är punkten diametralt mittemot $H$ . De tre 2-visa skärningspunkterna definierar figurens referenstriangel . Konceptet är uppkallat efter Roger Arthur Johnson.

Egenskaper

Johnson cirklar

J A ≅ J B ≅ J C

med radien

r

(skär varandra vid

H

; par skär varandra vid

A, B, C

)

Antikomplementär cirkel av

△ ABC

(radie

2 r

); tangent till Johnson-cirklarna vid

P A, P B, P C

Linjer mellan den gemensamma korsningen,

H

, och

P A, P B, P C

Antikomplementär triangel

△ P A P B P C

av

△ ABC

Centrum för Johnson-cirklarna ligger på en cirkel med samma radie $r$ som Johnson-cirklarna centrerade vid $H$ . Dessa centra bildar Johnson-triangeln .
Cirkeln centrerad vid $H$ med radien $2 r$ , känd som den antikomplementära cirkeln, tangerar var och en av Johnson-cirklarna. De tre tangentpunkterna är reflektioner av punkt $H$ runt hörnen på Johnson-triangeln.
Tangenspunkterna mellan Johnson-cirklarna och den antikomplementära cirkeln bildar en annan triangel, kallad referenstriangelns antikomplementära triangel . Den liknar Johnson-triangeln och är homotetisk med en faktor 2 centrerad vid $H$ , deras gemensamma circumcenter.
Johnsons sats : De 2-visa skärningspunkterna för Johnson-cirklarna (hörn i referenstriangeln $△ ABC$ ) ligger på en cirkel med samma radie $r$ som Johnson-cirklarna. Den här egenskapen är också välkänd i Rumänien som The 5 lei coin problem of Gheorghe Țițeica .
Referenstriangeln är i själva verket kongruent med Johnson-triangeln och är homotetisk till den med en faktor −1.
Punkten $H$ är referenstriangelns ortocentrum och Johnsontriangelns omkretscentrum .
Johnson-triangelns homotetiska centrum och referenstriangeln är deras gemensamma niopunktscentrum .

Bevis

Fastighet 1 framgår av definitionen. Egenskap 2 är också tydlig: för varje cirkel med radie $r$ och vilken punkt $P som helst$ på den, är cirkeln med radie $2 r$ centrerad vid $P$ tangent till cirkeln i dess punkt mitt emot $P$ ; detta gäller särskilt $P = H$ , vilket ger den antikomplementära cirkeln $C$ . Egenskap 3 i formuleringen av homoteten följer omedelbart; triangeln med tangenspunkter är känd som den antikomplementära triangeln.

För egenskaperna 4 och 5, observera först att två av de tre Johnson-cirklarna är utbytta av reflektionen i linjen som förbinder $H$ och deras 2-visa skärningspunkt (eller i deras gemensamma tangent vid $H$ om dessa punkter skulle sammanfalla), och denna reflektion byter också ut de två hörnen av den antikomplementära triangeln som ligger på dessa cirklar. Den 2-visa skärningspunkten är därför mittpunkten på en sida av den antikomplementära triangeln, och $H$ ligger på den vinkelräta bisektrisen på denna sida. Nu är mittpunkterna på sidorna av en triangel bilderna av dess hörn av en homotet med faktor −½, centrerad vid triangelns barycentrum. Tillämpad på den antikomplementära triangeln, som själv erhålls från Johnson-triangeln av en homotet med faktor 2, följer det av sammansättningen av homoter att referenstriangeln är homotetisk till Johnson-triangeln med en faktor −1. Eftersom en sådan homothety är en kongruens , ger detta egenskap 5, och även Johnson cirklar satsen eftersom kongruenta trianglar har omskrivna cirklar med lika radie.

För egenskap 6 var det redan fastställt att de vinkelräta bisektorerna för sidorna av den antikomplementära triangeln alla passerar genom punkten $H$ ; eftersom den sidan är parallell med en sida av referenstriangeln, är dessa vinkelräta bisektrar också referenstriangelns höjder .

Egenskap 7 följer omedelbart från egenskap 6 eftersom det homotetiska centret vars faktor är -1 måste ligga i mitten av omkretsarna $O$ i referenstriangeln och $H$ i Johnson-triangeln; den senare är referenstriangelns ortocentrum, och dess niopunktscentrum är känt för att vara den mittpunkten. Eftersom den centrala symmetrin också kartlägger referenstriangelns ortocentrum till Johnsontriangelns, är det homotetiska centret också Johnsontriangelns niopunktscentrum.

Det finns också ett algebraiskt bevis för Johnsons cirklarsats, med hjälp av en enkel vektorberäkning. Det finns vektorer ${\vec {u}},{\vec {v}},{\vec {w}},$ alla med längden $r$ , så att Johnson cirklar är centrerade vid ${\displaystyle H+{\vec {u}},H+{\vec {v}},H+{\vec {w}}.} Då är de 2-visa$ skärningspunkterna $H+{\vec {u}}+{\vec {v}},H+{\vec {u}}+{\vec {w}}, H+{\vec {v}}+{\vec {w}}$ och punkten $H+{\vec {u}}+{\vec {v}} +{\vec {w}}$ har tydligt avstånd $r$ till någon av dessa 2-visa skärningspunkter.

Ytterligare fastigheter

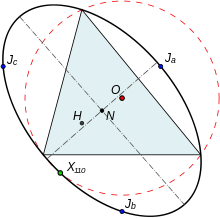
De tre Johnson-cirklarna kan betraktas som reflektioner av referenstriangelns omslutna cirkel kring var och en av de tre sidorna av referenstriangeln. Vidare, under reflektionerna kring referenstriangelns tre sidor, mappar dess ortocentrum $H$ till tre punkter på referenstriangelns omkretscirkel som bildar hörn av den circum-ortiska triangeln , dess omkretscentrum $O$ avbildas på hörnen av Johnsontriangeln och dess Euler-linje (linje som går genom $O, N, H$ ) genererar tre linjer som är samtidiga vid X (110).

Johnson cirkumkonisk

Johnsontriangeln och dess referenstriangel delar samma niopunktscentrum, samma Eulerlinje och samma niopunktscirkel . De sex punkterna som bildas från hörnen på referenstriangeln och dess Johnson-triangel ligger alla på Johnsons circumconic som är centrerad vid niopunktscentrumet och som har punkten X (216) i referenstriangeln som sin perspektör. Den circumkoniska och den omslutna cirklarn delar en fjärde punkt, X (110) i referenstriangeln.

Slutligen finns det två intressanta och dokumenterade circumcubics som passerar genom referenstriangelns sex hörn och dess Johnson-triangel samt circumcenter, ortocenter och niopunktscentrum. Den första är känd som den första Musselman-kubiken – K 026. Denna kubisk passerar också genom de sex hörnen i den mediala triangeln och den mediala triangeln i Johnson-triangeln. Den andra kubiken är känd som Eulers centrala kubik – K 044. Denna kubik passerar också genom de sex hörnen i den ortiska triangeln och den ortiska triangeln i Johnson-triangeln.

X ( i ) punktnotationen är Clark Kimberling ETC- klassificeringen av triangelcentrum.

externa länkar

Weisstein, Eric W. "Johnsons teorem" . MathWorld .
FM Jackson och Weisstein, Eric W. "Johnson Circles" . MathWorld .
FM Jackson och Weisstein, Eric W. "Johnson Triangle" . MathWorld .
Weisstein, Eric W. "Johnson Circumconic" . MathWorld .
Weisstein, Eric W. "Antikomplementär triangel" . MathWorld .
Weisstein, Eric W. "Circum-Orthic Triangle" . MathWorld .
Bernard Gibert Circumcubic K026
Bernard Gibert Circumcubic K044
Clark Kimberling, " Encyclopedia of triangle centers ". (Listar cirka 3000 intressanta punkter som är associerade med valfri triangel.)