Optiskt fasutrymme

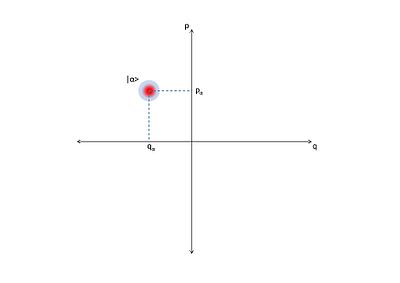
Optiskt fasdiagram över ett koherent tillstånds fördelning över fasutrymmet.

Inom kvantoptik är ett optiskt fasutrymme ett fasutrymme där alla kvanttillstånd i ett optiskt system beskrivs. Varje punkt i det optiska fasutrymmet motsvarar ett unikt tillstånd för ett optiskt system . För alla sådana system kallas en plot av kvadraturerna mot varandra, möjligen som funktioner av tid, ett fasdiagram . Om kvadraturerna är funktioner av tid kan det optiska fasdiagrammet visa utvecklingen av ett kvantoptiskt system med tiden.

Ett optiskt fasdiagram kan ge insikt i systemets egenskaper och beteenden som annars kanske inte är uppenbara. Detta kan anspela på egenskaper hos systemet som kan vara av intresse för en individ som studerar ett optiskt system som annars skulle vara mycket svåra att härleda. En annan användning för ett optiskt fasdiagram är att det visar utvecklingen av tillståndet hos ett optiskt system. Detta kan användas för att bestämma det optiska systemets tillstånd vid vilken tidpunkt som helst.

Bakgrundsinformation

När man diskuterar ljusets kvantteorin är det mycket vanligt att använda en elektromagnetisk oscillator som modell. En elektromagnetisk oscillator beskriver en oscillation av det elektriska fältet. Eftersom magnetfältet är proportionellt mot förändringshastigheten för det elektriska fältet, svänger även detta. Sådana svängningar beskriver ljus. System sammansatta av sådana oscillatorer kan beskrivas med ett optiskt fasutrymme.

Låt u ( x ,t) vara en vektorfunktion som beskriver en enkelmod för en elektromagnetisk oscillator . För enkelhetens skull antas det att denna elektromagnetiska oscillator är i vakuum. Ett exempel är den plana vågen som ges av

$\mathbf {u} (\mathbf {x} ,t)=\mathbf {u_{0}} e^{i(\ mathbf {k} \cdot \mathbf {x} -\omega t)}$

där u ₀ är polarisationsvektorn , k är vågvektorn , $\omega$ frekvensen och A $\cdot$ B anger punktprodukten mellan vektorerna A och B . Detta är ekvationen för en plan våg och är ett enkelt exempel på en sådan elektromagnetisk oscillator. Oscillatorerna som undersöks kan antingen vara fria vågor i rymden eller något normalt läge i något hålrum.

Ett enda läge för den elektromagnetiska oscillatorn isoleras från resten av systemet och undersöks. En sådan oscillator, när den är kvantiserad, beskrivs av matematiken för en kvantharmonisk oscillator . Kvantoscillatorer beskrivs med skapelse- och förintelseoperatorer ${\hat {a}}^{\dolk }$ och ${\hat {a}}$ . Fysiska storheter, såsom den elektriska fältstyrkan , blir sedan kvantoperatorer .

För att skilja en fysisk storhet från den kvantmekaniska operatorn som används för att beskriva den, används en "hatt" över operatorsymbolerna. Således, till exempel, där $E_{i}$ kan representera (en komponent av) det elektriska fältet , betecknar symbolen ${\widehat {E}}_{i}$ kvantum -mekanisk operator som beskriver $E_{i}$ . Denna konvention används genomgående i den här artikeln, men är inte vanligt förekommande i mer avancerade texter, som undviker hatten, eftersom den helt enkelt rör ihop texten.

I kvantoscillatorläget uttrycks de flesta operatorer som representerar fysiska storheter vanligtvis i termer av skapande och förintelseoperatorer. I detta exempel ges den elektriska fältstyrkan av:

${\widehat {E}}_{i}=u_{i}^{*}(\ mathbf {x} ,t){\widehat {a}}^{\dolk }+u_{i}(\mathbf {x} ,t){\widehat {a}}$

(där x _i är en enkel komponent av x , position). Hamiltonian för en elektromagnetisk oscillator hittas genom att kvantisera det elektromagnetiska fältet för denna oscillator och formeln ges av :

${\widehat {H}}=\hbar \omega ({\widehat {a}}^{\dolk }{\widehat {a} }+1/2)$

där $\omega$ är frekvensen för det (spatio-temporala) läget. Förintelseoperatorn är den bosoniska förintelseoperatorn och därför följer den den kanoniska kommuteringsrelationen som ges av:

$[{\widehat {a}},{\widehat {a}}^{\dolk }]=1$

Egentillstånden för annihilationsoperatorn kallas koherenta tillstånd :

${\widehat {a}}|\alpha \rangle =\alpha |\alpha \rangle$

Det är viktigt att notera att annihilationsoperatören inte är hermitisk ; därför kan dess egenvärden $\alpha$ vara komplexa. Detta får viktiga konsekvenser.

Slutligen ges fotonnumret av operatorn ${\widehat {N}}={\widehat {a}}^{\dolk }{\widehat {a}},$ som ger antalet fotoner i det givna (spatial-temporala) läget u .

Kvadraturer

Operatörer ges av

${\widehat {q}}={\tfrac {1}{2}}({\widehat {a}}^{\dolk }+{\ bredhatt {a}})$

och

${\widehat {p}}={\tfrac {i}{2}}({\widehat {a}}^{\dolk }-{\ bredhatt {a}})$

kallas kvadraturerna och de representerar de reella och imaginära delarna av den komplexa amplituden som representeras av ${\widehat {a}}$ . Kommuteringsrelationen mellan de två kvadraturerna kan enkelt beräknas:

${\begin{aligned}\left[{\widehat {q}}, {\widehat {p}}\right]&={\tfrac {i}{4}}[{\widehat {a}}^{\dolk }+{\widehat {a}},{\widehat {a} }^{\dolk }-{\widehat {a}}]\\&={\tfrac {i}{4}}([{\widehat {a}}^{\dolk },{\widehat {a} }^{\dolk }]-[{\widehat {a}}^{\dolk },{\widehat {a}}]+[{\widehat {a}},{\widehat {a}}^{\ dolk }]-[{\widehat {a}},{\widehat {a}}])\\&={\tfrac {i}{4}}(-(-1)+1)\\&={ \tfrac {i}{2}}\end{aligned}}$

Detta liknar kommuteringsrelationen för positions- och momentumoperatorn. Sålunda kan det vara användbart att tänka på och behandla kvadraturerna som positionen och rörelsemängden för oscillatorn, även om de i själva verket är "i-fas- och ur-fas-komponenterna av det elektriska fältets amplitud för det rumsliga-temporala läget" , eller u , och har egentligen ingenting att göra med den elektromagnetiska oscillatorns position eller momentum (eftersom det är svårt att definiera vad som menas med position och momentum för en elektromagnetisk oscillator).

Egenskaper för kvadraturer

Egentillstånden för kvadraturoperatorerna $widehat {q}}}$ \ och ${\widehat {p}}$ kallas kvadraturtillstånden. De uppfyller relationerna:

• ${\widehat {q}}|q\rangle =q|q\rangle$ och ${\widehat {p}}|p\rangle =p|p\rangle$

• $\langle q|q'\rangle =\delta (qq')$ och $\langle p|p'\rangle =\delta (pp')$

• $\int _{-\infty }^{\infty }|q\rangle \langle q|\,dq=1$ och $\int _{-\infty }^{\infty }|p\rangle \langle p|\,dp=1$

eftersom dessa utgör kompletta basuppsättningar.

Viktigt resultat

Följande är en viktig relation som kan härledas från det ovanstående som motiverar vår tolkning att kvadraturerna är de verkliga och imaginära delarna av en komplex $\alpha$ (dvs. i-fas och ut-av-fas komponenter av den elektromagnetiska oscillatorn)

$\langle \alpha |{\widehat {q}}|\alpha \rangle =2^{-1/2}(\langle \alpha |{\widehat {a}}^{\dolk }|\alpha \rangle +\langle \alpha |{\widehat {a}}|\alpha \rangle )=2^{-1/2}(\alpha ^{*}\langle \alpha |\alpha \rangle +\alpha \ langle \alpha |\alpha \rangle )$

Följande är en relation som kan användas för att utvärdera ovanstående och ges av:

$\langle \alpha '|\alpha \rangle =e^{(-1/2) (|\alpha '|^{2}+|\alpha |^{2})+\alpha '^{*}\alpha }$

Detta ger oss att:

$\langle \alpha |{\widehat {q}}|\alpha \rangle =2^{-1/2}(\alpha ^ {*}+\alpha )=q_{\alpha }$

$\langle \alpha |{\widehat {p}}|\alpha \rangle =i2^{-1/2}(\alpha ^{*}-\alpha )=p_{\alpha }$ med en liknande metod som ovan.

$\alpha =2^{ -1/2}(\langle \alpha |{\widehat {q}}|\alpha \rangle +i\langle \alpha |{\widehat {p}}|\alpha \rangle )=2^{-1/ 2}(q_{\alpha }+ip_{\alpha })$

Således är $\alpha$ bara en sammansättning av kvadraturerna.

En annan mycket viktig egenskap hos de koherenta staterna blir mycket uppenbar i denna formalism. Ett koherent tillstånd är inte en punkt i det optiska fasutrymmet utan snarare en fördelning på det. Detta kan ses via

$q_{\alpha }=\langle \alpha |{\widehat {q}}|\alpha \rangle$

och

$p_{\alpha }=\langle \alpha |{\widehat {p}}|\alpha \rangle$ .

Dessa är endast förväntade värden för ${\widehat {q}}$ och ${\widehat {p}}$ för staten $|\alpha \rangle$ .

Det kan visas att kvadraturerna följer Heisenbergs osäkerhetsprincip som ges av:

$\Delta q\Delta p\geq 1/2$ (där $\Delta q$ och $\Delta p$ är varianserna för fördelningarna av q respektive p)

Denna ojämlikhet behöver inte nödvändigtvis vara mättad och ett vanligt exempel på sådana tillstånd är sammanpressade tillstånd . De koherenta tillstånden är gaussiska sannolikhetsfördelningar över fasutrymmet lokaliserade runt $\alpha$ .

Operatörer på fasutrymme

Det är möjligt att definiera operatorer för att flytta de koherenta tillstånden runt fasrummet. Dessa kan producera nya koherenta tillstånd och tillåta oss att röra oss i fasrummet.

Fasskiftande operatör

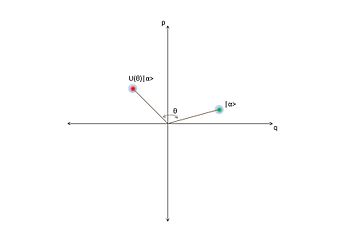
Fasskiftningsoperator som verkar på ett koherent tillstånd och roterar det med en vinkel $\theta$ i fasrymden.

Den fasskiftande operatorn roterar det koherenta tillståndet med en vinkel $\theta$ i det optiska fasutrymmet. Denna operatör ges av:

${\widehat {U}}(\theta )=e^{-i\theta {\widehat {N}}}$

Den viktiga relationen

${\widehat {U}}(\theta )^{\dolk }{\widehat {a}}{\widehat { U}}(\theta )={\widehat {a}}e^{-i\theta }$

härleds enligt följande:

${ \displaystyle d/d\theta ({\widehat {U}}^{\dolk }{\widehat {a}}{\widehat {U}})=i{\widehat {N}}{\widehat {U} }^{\dolk }{\widehat {a}}{\widehat {U}}-i{\widehat {U}}^{\dolk }{\widehat {a}}{\widehat {U}}{\ widehat {N}}={\widehat {U}}^{\dolk }i[{\widehat {N}},{\widehat {a}}]{\widehat {U}}}$

$={ \widehat {U}}^{\dolk }i({\widehat {a}}^{\dolk }{\widehat {a}}{\widehat {a}}-{\widehat {a}}{\widehat {a}}^{\dolk }{\widehat {a}}){\widehat {U}}={\widehat {U}}^{\dolk }i[{\widehat {a}}^{\dolk },{\widehat {a}}]{\widehat {a}}{\widehat {U}}=-i{\widehat {U}}^{\dolk }{\widehat {a}}{\widehat { U}}$

och att lösa denna differentialekvation ger det önskade resultatet.

Med hjälp av ovanstående blir det alltså tydligt att

${\widehat {U}}(\theta )|\alpha \rangle =|\alpha e^{-i\theta }\rangle$ ,

eller en rotation med en vinkel theta på det koherenta tillståndet i fasrummet. Följande illustrerar detta tydligare:

${\widehat {a}}({\widehat {U}}|\alpha \rangle )={\widehat {U}}{\widehat {a}}e^{-i\theta }| \alpha \rangle$

(vilket erhålls genom att använda det faktum att den fasskiftande operatorn är enhetlig

${\widehat {a}}({\widehat {U}}|\alpha \rangle )={\widehat {U}}\alpha e ^{-i\theta }|\alpha \rangle =\alpha e^{-i\theta }({\widehat {U}}|\alpha \rangle )$

Således,

$(\alpha e^{-i\theta },{\widehat {U}}|\alpha \rangle )$

är egenparet till

${\widehat {a}}{\widehat {U}}|\alpha \rangle$ .

Av detta är det möjligt att se det

$(\alpha e^{-i\theta }=2^{-1/2}[q_{\alpha }\cos (\theta )+p_{\alpha }\sin(\theta )]+i2^{-1/2}[-q_{\alpha }\sin(\theta )+p_{\alpha }\cos(\theta )],{\widehat {U}}|\alpha \rangle =|\alpha e^{-i\theta }\rangle )$

vilket är ett annat sätt att uttrycka egenparet som tydligare illustrerar effekterna av den fasskiftande operatorn på koherenta tillstånd.

Förskjutningsoperatör

Förskjutningsoperator som verkar på ett koherent tillstånd som förskjuter det med något värde $\alpha$ i fasrymden.

Förskjutningsoperatorn är en enhetlig operator som tar ett koherent tillstånd och förvandlar det till ett annat koherent tillstånd. Förskjutningsoperatorn ges av

${\widehat {D}}(\alpha )=e^{\alpha {\widehat {a}}^{\dolk }-\ alfa ^{*}{\widehat {a}}}$

och dess namn kommer från en viktig relation

${\widehat {a}}(\alpha )\equiv {\widehat {D}}^{\ dolk }(\alpha ){\widehat {a}}{\widehat {D}}(\alpha )={\widehat {a}}+\alpha$ .

Låt oss faktiskt tillfälligt introducera ${\widehat {a}}(s)={\widehat {a}}(s\alpha )$ med riktig $s$ och fundera över hur ${\widehat {\widehat {a}}(s)}$ varierar när $s$ ändras från 0 till 1. Differentiera ${\widehat {a}}(s)$ med avseende på $s$ , finner vi

${\frac {\partial }{\partial s}}{\widehat {a}}(s)=D^{\dolk }(s\alpha )[\alpha ^{*}{\widehat {a}}-\alpha {\widehat {a}}^ {\dolk },{\widehat {a}}]D(s\alpha )=\alpha ,$

så att ${\widehat {a}}(s)={\widehat {a}}(0)+s\alpha .$

Eftersom koherenta tillstånd är egentillstånd för både annihilationsoperatorn och operatorn för multiplikation med ett tal, är det lätt att se att förskjutningsoperatorn faktiskt flyttar de koherenta tillstånden, eller, mer exakt,

${\widehat {D}}(\alpha )|\beta \rangle =|\alpha +\beta \rangle .$

Relationen härledd ovan kan faktiskt skrivas om som ${\displaystyle {\widehat {a}}{\widehat {D}}(\alpha ) ={\widehat {D}}(\alpha )({\widehat {a}}+\alpha )} ,$ sedan

${\widehat {a}}{\widehat {D}}(\alpha )|\beta \rangle ={\widehat {D}}(\alpha )({\widehat {a}}+\alpha ) |\beta \rangle =(\alpha +\beta ){\widehat {D}}(\alpha )|\beta \rangle .$

${\widehat {D}}(\alpha )|\beta \rangle$ _ är ett egentillstånd för annihilationsoperatorn med egenvärdet $\alpha +\beta$ , därav ${\widehat {D}}(\alpha )|\beta \rangle =|\alpha +\beta \rangle$ .

Särskilt,

${\widehat {D}}(-\alpha )|\alpha \rangle =|0\rangle$

som leder till

$|\alpha \rangle ={\widehat {D}}(\alpha )|0\rangle$ .

Detta är viktigt eftersom det visar att alla koherenta tillstånd kan erhållas som förskjutningar av grundtillståndet, vilket inom optik också är vakuumtillståndet .

Se även

• Icke klassiskt ljus
• Rotationsoperatör (kvantmekanik)
• Kvantharmonisk oscillator
• Kvasisannolikhetsfördelning
• Husimi Q representation
• Pressat sammanhängande tillstånd
• Wigner kvasisannolikhetsfördelning