Lorenz system

Ej att förväxla med Lorenz-kurvan eller Lorentz-fördelningen .

En provlösning i Lorenz-attraktorn när β = 8/3 ρ 10 = 28 , σ = och

Lorenzsystemet är ett system av vanliga differentialekvationer som först studerades av matematikern och meteorologen Edward Lorenz . Det är anmärkningsvärt för att ha kaotiska lösningar för vissa parametervärden och initiala förhållanden. I synnerhet Lorenz-atttraktorn en uppsättning kaotiska lösningar av Lorenz-systemet. I populära medier härrör " fjärilseffekten " från de verkliga implikationerna av Lorenz-atttraktorn, nämligen den i ett kaotiskt fysiskt system, i avsaknad av perfekt kunskap om de initiala förhållandena (även den minimala störningen av luften på grund av en fjäril flaxar med vingarna), kommer vår förmåga att förutsäga dess framtida kurs alltid att misslyckas. Detta understryker att fysiska system kan vara helt deterministiska och ändå vara i sig oförutsägbara. Formen på själva Lorenz-atttraktorn, när den plottas i fasrymden , kan också ses likna en fjäril.

Översikt

År 1963 utvecklade Edward Lorenz , med hjälp av Ellen Fetter som var ansvarig för de numeriska simuleringarna och siffrorna, och Margaret Hamilton som hjälpte till i de inledande, numeriska beräkningarna som ledde fram till upptäckten av Lorenzmodellen, en förenklad matematisk modell för atmosfäriska konvektion . Modellen är ett system av tre vanliga differentialekvationer som nu kallas Lorenz-ekvationerna:

${\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma (yx),\\[6pt]{\frac {\mathrm {d } y}{\mathrm {d} t}}&=x(\rho -z)-y,\\[6pt]{\frac {\mathrm {d} z}{\mathrm {d} t}}& =xy-\beta z.\end{aligned}}$

Ekvationerna relaterar egenskaperna hos ett tvådimensionellt vätskeskikt likformigt uppvärmt underifrån och kylt uppifrån. Speciellt beskriver ekvationerna förändringshastigheten för tre storheter med avseende på tid: x är proportionell mot konvektionshastigheten, y mot den horisontella temperaturvariationen och z mot den vertikala temperaturvariationen. Konstanterna σ , ρ och β är systemparametrar som är proportionella mot Prandtl-talet , Rayleigh-talet och vissa fysiska dimensioner av själva lagret.

Lorenz-ekvationerna kan uppstå i förenklade modeller för lasrar , dynamos , termosyfoner , borstlösa DC-motorer , elektriska kretsar , kemiska reaktioner och framåtosmos . Lorenz-ekvationerna är också de styrande ekvationerna i Fourierrymden för Malkus vattenhjul . Malkus vattenhjul uppvisar kaotiska rörelser där istället för att snurra i en riktning med konstant hastighet, kommer dess rotation att påskynda, sakta ner, stanna, ändra riktning och pendla fram och tillbaka mellan kombinationer av sådana beteenden på ett oförutsägbart sätt.

Ur teknisk synvinkel är Lorenz-systemet olinjärt , aperiodiskt, tredimensionellt och deterministiskt . Lorenz-ekvationerna har varit föremål för hundratals forskningsartiklar och minst en boklängdsstudie.

Analys

Man antar normalt att parametrarna σ , ρ , och β är positiva. Lorenz använde värdena σ = 10 , β = 8 / 3 och ρ = 28 . Systemet uppvisar kaotiskt beteende för dessa (och närliggande) värden.

Om ρ < 1 så finns det bara en jämviktspunkt, som är vid origo. Denna punkt motsvarar ingen konvektion. Alla banor konvergerar till ursprunget, som är en global attraktion , när ρ < 1 .

En höggaffelförgrening inträffar vid ρ = 1 , och för ρ > 1 visas ytterligare två kritiska punkter vid

$$\left({\sqrt {\beta (\rho -1)}},{\sqrt {\beta (\rho -1)}},\rho -1\right)\quad {\text{and }}\quad \left(-{\sqrt {\beta (\rho -1)}},-{\sqrt {\beta (\rho -1)}},\rho -1\right).$$

Dessa motsvarar stadig konvektion. Detta par av jämviktspunkter är stabilt endast om

$\rho <\sigma {\frac {\sigma +\beta +3}{\sigma -\beta - 1}},$

som bara kan gälla för positivt ρ om σ > β + 1 . Vid det kritiska värdet förlorar båda jämviktspunkterna stabilitet genom en subkritisk Hopf-bifurkation .

När ρ = 28 , σ = 10 , och β = 8 / 3 , har Lorenz-systemet kaotiska lösningar (men inte alla lösningar är kaotiska). Nästan alla initiala punkter kommer att tendera till en invariant uppsättning – Lorenz-attraktorn – en konstig atttraktor , en fraktal och en självexciterad attraktion med avseende på alla tre jämvikter. Dess Hausdorff-dimension uppskattas ovanifrån av Lyapunov-dimensionen (Kaplan-Yorke-dimensionen) till 2,06 ± 0,01 , och korrelationsdimensionen uppskattas till 2,05 ± 0,01 . Den exakta Lyapunov-dimensionsformeln för den globala attraktionen kan hittas analytiskt under klassiska begränsningar av parametrarna:

$3-{\frac {2(\sigma +\beta +1)}{\sigma +1+ {\sqrt {\left(\sigma -1\right)^{2}+4\sigma \rho }}}}$

Lorenz-attraktorn är svår att analysera, men differentialekvationens verkan på atttraktorn beskrivs av en ganska enkel geometrisk modell. Att bevisa att så verkligen är fallet är det fjortonde problemet på listan över Smales problem . Detta problem var det första som löstes, av Warwick Tucker 2002.

För andra värden på ρ visar systemet knutna periodiska banor. Till exempel, med ρ = 99,96 blir det en T (3,2) torusknut .

Exempel på lösningar av Lorenz-systemet för olika värden på ρ
ρ = 14, σ = 10, β = 8/3 förstora ) (	ρ = 13, σ = 10, β = 8/3 förstora ) (
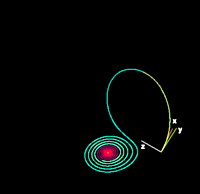
ρ = 15, σ = 10, β = 8/3 Förstora ) (	ρ = 28, σ = 10, β = 8/3 förstora ) (
För små värden på ρ är systemet stabilt och utvecklas till en av två fastpunktsatttraktorer. När ρ > 24,74 blir de fixerade punkterna repulsorer och banan stöts bort av dem på ett mycket komplext sätt.

Känsligt beroende av initialtillståndet
Tid t = 1 (Förstora)	Tid t = 2 (Förstora)	Tid t = 3 (Förstora)
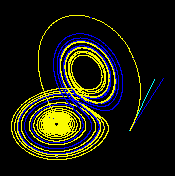
Dessa figurer – gjorda med ρ = 28 , σ = 10 och β = 8 / 3 – visar tre tidssegment av 3D-utvecklingen av två banor (en i blått, den andra i gult) i Lorenz-attraktorn med start vid två initiala punkter som endast skiljer sig med 10 −5 i x -koordinaten. Inledningsvis verkar de två banorna sammanfalla (endast den gula kan ses, eftersom den är ritad över den blå) men efter en tid är skillnaden uppenbar.

Anslutning till tältkarta

En återskapande av Lorenzs resultat skapade på Mathematica . Punkter ovanför den röda linjen motsvarar systemets kopplingslober.

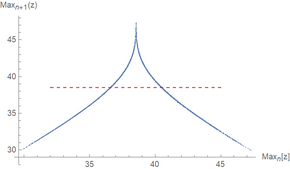
I figur 4 i hans papper plottade Lorenz det relativa maximala värdet i z-riktningen som uppnåtts av systemet mot det tidigare relativa maximum i z- riktningen . Denna procedur blev senare känd som en Lorenz-karta (inte att förväxla med en Poincaré-plot , som plottar skärningspunkterna för en bana med en föreskriven yta). Den resulterande tomten har en form som mycket liknar tältkartan . Lorenz fann också att när det maximala z- värdet är över en viss cut-off kommer systemet att växla till nästa lob. Genom att kombinera detta med det kaos som tältkartan känner till visade han att systemet växlar mellan de två loberna kaotiskt.

Ett generaliserat Lorenz-system

Under de senaste åren har en serie artiklar om högdimensionella Lorenz-modeller gett en generaliserad Lorenz-modell, som kan förenklas till den klassiska Lorenz-modellen för tre tillståndsvariabler eller följande femdimensionella Lorenz-modell för fem tillståndsvariabler:

$${\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma (yx),\\[6pt]{\frac {\mathrm {d } y}{\mathrm {d} t}}&=x(\rho -z)-y,\\[6pt]{\frac {\mathrm {d} z}{\mathrm {d} t}}& =xy-xy_{1}-\beta z,\\[6pt]{\frac {\mathrm {d} y_{1}}{\mathrm {d} t}}&=xz-2xz_{1}-d_ {0}y_{1},\\[6pt]{\frac {\mathrm {d} z_{1}}{\mathrm {d} t}}&=2xy_{1}-4\beta z_{1} .\end{aligned}}$$

₀ Ett val av parametern d = 19/3 har tillämpats för att överensstämma med valet av de andra parametrarna. Se detaljer i.

Simuleringar

 
     
     
     
     
     
     
    
          
           
           
           
         
         
         
          
             0
           
           
      
        
   
        def  newton_raphson  (  f  ,  g  ,  e  ,  x0  ,  N  ):  x0  =  flagga  (  x0  )  e  =  flagga  (  e  )  N  =  int  (  N  )  steg  =  1  flagga  =  1  villkor  =  Sant  medan  villkor  :  om  g  (  x0  )  = =  0.0  :  skriv ut  (  'dividera med noll'  )  bryt  x1  =  x0  -  f  (  x0  )  /  g  (  x0  )  skriv ut  (  'iteration  %d  , x1=  %0.6f  och f(x0)=  %0.6f  '  %  (  steg  ,  x1  ,  f  (  x1  )))  x0  =  x1  steg  +=  1  om  steg  >  N  :  flagga  =  brytvillkor  =  abs  (  f  (  x1  )  )  >  e  om  flagga  ==  1  :  print  (  '  \n  den nödvändiga roten är 0,8f'  %  x1  )  annat  :  print  (  '  \n  inte konvergent'  ) 

MATLAB-simulering

  
  
  
             
  0        
 % Lös över tidsintervall [0,100] med initiala villkor [1,1,1]  % ''f'' är en uppsättning differentialekvationer  % ''a'' är matris som innehåller x-, y- och z-variabler  % ''t' ' är tidsvariabel  sigma  =  10  ;  beta  =  8/3  ;  _  _  rho  =  28  ;  f  =  @(  t  ,  a  )  [  -sigma  *  a  (  1  )  +  sigma  *  a  (  2  )  ;  rho  *  a  (  1  )  -a  (  2  )  -a  (  1  )  *  a  (  3  )  ;  _  -  beta  *  a  (  3  )  +  a  (  1  )  *  a  (  2  )];  [  t  ,  a  ]  =  ode45  (  f  ,[  100  ],[  111  ]  )  ;  % Runge-Kutta 4:e/5:e ordningens ODE-lösare  plot3  (  a  (:,  1  ),  a  (:,  2  ),  a  (:,  3  )) 

Mathematica simulering

Standardsätt:

  
        
              
            
  0   0   0  
    
    
          0 
    0  tenderar  =  50  ;  ekv  =  {  x  '  [  t  ]  ==  σ  (  y  [  t  ]  -  x  [  t  ]),  y  '  [  t  ]  ==  x  [  t  ]  (  ρ  -  z  [  t  ])  -  y  [  t  ],  z  '  [  t  ]  ==  ​​x  [  t  ]  y  [  t  ]  -pz  [  t  ]  }  ;  init  =  {  x  [  ]  ==  10  ,  y  [  ]  ==  10  ,  z  [  ]  ==  10  };  pars  =  {  σ  ->  10  ,  ρ  ->  28  ,  β  -  >  8/3  }  ;  {  xs  ,  ys  ,  zs  }  =  NDSolveValue  [{  eq  /.  pars  ,  init  },  {  x  ,  y  ,  z  },  {  t  ,  ,  tender  }];  ParametricPlot3D  [{  xs  [  t  ],  ys  [  t  ],  zs  [  t  ]},  {  t  ,  ,  tenderar  }] 

Mindre utförlig:

                       
          0 
  0  lorenz  =  NolinearStateSpaceModel  [{{  σ  (  y  -  x  ),  x  (  ρ  -  z  )  -  y  ,  x  y  -  β  z  },  {}},  {  x  ,  y  ,  z  },  {  σ  ,  ρ  ,  β  }];  soln  [  t_  ]  =  StateResponse  [{  lorenz  ,  {  10  ,  10  ,  10  }},  {  10  ,  28  ,  8/3  }  ,  {  t  ,,  50  }  ]  ;  ParametricPlot3D  [  soln  [  t  ],  {  t  ,  ,  50  }] 

Ansökningar

Modell för atmosfärisk konvektion

Som framgår av Lorenz originaltidning är Lorenz-systemet en reducerad version av ett större system som tidigare studerats av Barry Saltzman. Lorenz-ekvationerna är härledda från Oberbeck-Boussinesq-approximationen till ekvationerna som beskriver vätskecirkulation i ett grunt lager av vätska, uppvärmd likformigt underifrån och kyld likformigt ovanifrån. Denna vätskecirkulation är känd som Rayleigh-Bénard konvektion . Vätskan antas cirkulera i två dimensioner (vertikal och horisontell) med periodiska rektangulära gränsförhållanden.

De partiella differentialekvationerna som modellerar systemets strömfunktion och temperatur utsätts för en spektral Galerkin-approximation : de hydrodynamiska fälten expanderas i Fourier-serier, som sedan kraftigt trunkeras till en enda term för strömfunktionen och två termer för temperaturen. Detta reducerar modellekvationerna till en uppsättning av tre kopplade, olinjära vanliga differentialekvationer. En detaljerad härledning kan till exempel hittas i olinjära dynamiktexter från Hilborn (2000), Appendix C; 1984 Bergé, Pomeau & Vidal (1984) , Appendix D; eller Shen (2016), Kompletterande material.

Modell för karaktären av kaos och ordning i atmosfären

Det vetenskapliga samfundet accepterar att de kaotiska egenskaperna som finns i lågdimensionella Lorenz-modeller kan representera egenskaper hos jordens atmosfär (), vilket ger uttalandet om "vädret är kaotiskt." Som jämförelse, baserat på konceptet attraherande samexistens inom den generaliserade Lorenz-modellen och den ursprungliga Lorenz-modellen (), föreslog Shen och hans medförfattare en reviderad syn på att "vädret har både kaos och ordning med distinkt förutsägbarhet". Den reviderade uppfattningen, som är en uppbyggnad av den konventionella uppfattningen, används för att föreslå att "de kaotiska och regelbundna egenskaper som finns i teoretiska Lorenz-modeller bättre skulle kunna representera egenskaper hos jordens atmosfär".

Lösning av Smales 14:e problem

Smales 14:e problem säger: "Uppvisar egenskaperna hos Lorenz-atttraktorn egenskaperna hos en konstig atttraktor ?". Problemet besvarades jakande av Warwick Tucker 2002. För att bevisa detta resultat använde Tucker rigorösa numeriska metoder som intervallaritmetik och normala former . Först definierade Tucker ett tvärsnitt $\Sigma \subset \{x_{3}=r-1\}$ som skärs tvärs av flödesbanorna. Från detta kan man definiera första-retur-kartan $P$ , som tilldelar varje $x\in \Sigma$ punkten $P(x)$ där bana för $x$ skär först $\Sigma$ .

Sedan delas beviset upp i tre huvudpunkter som är bevisade och antyder att det finns en konstig attraktion. De tre punkterna är:

• Det finns en region $N\subset \Sigma$ invariant under första-retur-kartan, vilket betyder $P(N)\subset N$ .
• Returkartan tillåter ett framåt invariant konfält.
• Vektorer inuti detta invarianta konfält expanderas enhetligt med derivatan $DP$ av returkartan.

För att bevisa den första punkten lägger vi märke till att tvärsnittet $\Sigma$ skärs av två bågar som bildas av $P(\Sigma )$ . Tucker täcker platsen för dessa två bågar med små rektanglar $R_{i}$ , föreningen av dessa rektanglar ger $N$ . Nu är målet att bevisa att för alla punkter i $N$ kommer flödet att ta tillbaka punkterna i ${\displaystyle \Sigma } ,$ i $N$ . För att göra det tar vi en plan $\Sigma '$ under $\Sigma$ på ett avstånd $h$ litet, sedan genom att ta mitten $c_{i}$ av $R_{i}$ och med Euler-integreringsmetoden kan man uppskatta var flödet kommer att ge $c_{i}$ i $\Sigma '$ vilket ger oss en ny punkt $c_{i}'$ . Sedan kan man uppskatta var punkterna i $\Sigma$ kommer att mappas i $\Sigma '$ med hjälp av Taylor-expansion, detta ger oss en ny rektangel $R_{i}'$ centrerad på $c_{i}$ . Vi vet alltså att alla punkter i $R_{i}$ kommer att mappas i $R_{i}'$ . Målet är att göra denna metod rekursivt tills flödet kommer tillbaka till $\Sigma$ och vi får en rektangel $Rf_{i}$ i $\Sigma$ så att vi vet att $P(R_{i})\subset Rf_{i}$ . Problemet är att vår uppskattning kan bli oprecis efter flera iterationer, så det Tucker gör är att dela upp $R_{i}'$ i mindre rektanglar $R_{i,j$ } tillämpa sedan processen rekursivt. Ett annat problem är att när vi tillämpar denna algoritm blir flödet mer "horisontellt", vilket leder till en dramatisk ökning av oprecisionen. För att förhindra detta ändrar algoritmen orienteringen av tvärsnitten och blir antingen horisontell eller vertikal.

Galleri

• 

  En lösning i Lorenz-atttraktorn plottad med hög upplösning i xz -planet.

• 

  En lösning i Lorenz-atttraktorn renderad som en SVG .

• En animation som visar banor för flera lösningar i ett Lorenz-system.

• 

  En lösning i Lorenz-atttraktorn renderad som en metalltråd för att visa riktning och 3D -struktur.

• En animation som visar divergensen mellan närliggande lösningar till Lorenz-systemet.

• 

  En visualisering av Lorenz-atttraktorn nära en intermittent cykel.

• 

  Två strömlinjer i ett Lorenz-system, från ρ = 0 till ρ = 28 ( σ = 10 , β = 8 / 3 ).

• 

  Animation av ett Lorenz-system med rho-beroende.

• 

  Animation av Lorenz-atttraktorn i Brain Dynamics Toolbox.

Se även

• Edens gissningar om Lyapunov-dimensionen
• Lorenz 96 modell
• Lista över kaotiska kartor
• Takens sats

Anteckningar

•   Bergé, Pierre; Pomeau, Yves; Vidal, Christian (1984). Ordning inom kaos: Mot en deterministisk syn på turbulens . New York: John Wiley & Sons . ISBN 978-0-471-84967-4 .
•    Cuomo, Kevin M.; Oppenheim, Alan V. (1993). "Kretsimplementering av synkroniserat kaos med applikationer för kommunikation". Fysiska granskningsbrev . 71 (1): 65–68. Bibcode : 1993PhRvL..71...65C . doi : 10.1103/PhysRevLett.71.65 . ISSN 0031-9007 . PMID 10054374 .
• Gorman, M.; Widmann, PJ; Robbins, KA (1986). "Icke-linjär dynamik i en konvektionsslinga: En kvantitativ jämförelse av experiment med teori". Physica D . 19 (2): 255–267. Bibcode : 1986PhyD...19..255G . doi : 10.1016/0167-2789(86)90022-9 .
• Grassberger, P.; Procaccia, I. (1983). "Mätning av konstiga attraktionskrafter". Physica D . 9 (1–2): 189–208. Bibcode : 1983PhyD....9..189G . doi : 10.1016/0167-2789(83)90298-1 .
• Haken, H. (1975). "Analogi mellan högre instabiliteter i vätskor och lasrar". Fysik Bokstäver A . 53 (1): 77–78. Bibcode : 1975PhLA...53...77H . doi : 10.1016/0375-9601(75)90353-9 .
•   Hemati, N. (1994). "Konstiga atttraktorer i borstlösa DC-motorer". IEEE-transaktioner på kretsar och system I: Grundläggande teori och tillämpningar . 41 (1): 40–45. doi : 10.1109/81.260218 . ISSN 1057-7122 .
•   Hilborn, Robert C. (2000). Kaos och icke-linjär dynamik: en introduktion för forskare och ingenjörer ( andra upplagan). Oxford University Press . ISBN 978-0-19-850723-9 .
•   Hirsch, Morris W. ; Smale, Stephen ; Devaney, Robert (2003). Differentialekvationer, dynamiska system och en introduktion till kaos (andra upplagan). Boston, MA: Academic Press . ISBN 978-0-12-349703-1 .
• Knobloch, Edgar (1981). "Kaos i den segmenterade skivdynamon". Fysik Bokstäver A . 82 (9): 439–440. Bibcode : 1981PhLA...82..439K . doi : 10.1016/0375-9601(81)90274-7 .
•   Kolář, Miroslav; Gumbs, Godfrey (1992). "Teori för experimentell observation av kaos i ett roterande vattenhjul". Fysisk granskning A . 45 (2): 626–637. Bibcode : 1992PhRvA..45..626K . doi : 10.1103/PhysRevA.45.626 . PMID 9907027 .
•   Leonov, GA; Kuznetsov, NV; Korzhmanova, NA; Kusakin, DV (2016). "Lyapunov dimensionsformel för Lorenz-systemets globala attraktion". Kommunikation i icke-linjär vetenskap och numerisk simulering . 41 : 84–103. arXiv : 1508.07498 . Bibcode : 2016CNSNS..41...84L . doi : 10.1016/j.cnsns.2016.04.032 . S2CID 119614076 .
• Lorenz, Edward Norton (1963). "Deterministiskt icke-periodiskt flöde" . Journal of the Atmospheric Sciences . 20 (2): 130–141. Bibcode : 1963JAtS...20..130L . doi : 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 .
•   Mishra, Aashwin; Sanghi, Sanjeev (2006). "En studie av det asymmetriska Malkus-vattenhjulet: De partiska Lorenz-ekvationerna". Kaos: En tvärvetenskaplig tidskrift för icke-linjär vetenskap . 16 (1): 013114. Bibcode : 2006Chaos..16a3114M . doi : 10.1063/1.2154792 . PMID 16599745 .
•   Pchelintsev, AN (2014). "Numerisk och fysisk modellering av Lorenz-systemets dynamik". Numerisk analys och tillämpningar . 7 (2): 159–167. doi : 10.1134/S1995423914020098 . S2CID 123023929 .
• Polen, Douglas (1993). "Kooperativ katalys och kemiskt kaos: en kemisk modell för Lorenz-ekvationerna". Physica D . 65 (1): 86–99. Bibcode : 1993PhyD...65...86P . doi : 10.1016/0167-2789(93)90006-M .
• Saltzman, Barry (1962). "Fri konvektion med ändlig amplitud som ett initialt värdeproblem—I" . Journal of the Atmospheric Sciences . 19 (4): 329–341. Bibcode : 1962JAtS...19..329S . doi : 10.1175/1520-0469(1962)019<0329:FAFCAA>2.0.CO;2 .
• Shen, B.-W. (2015-12-21). "Icke-linjär återkoppling i en sexdimensionell Lorenz-modell: påverkan av en ytterligare värmeterm". Icke-linjära processer i geofysik . 22 (6): 749–764. doi :10.5194/npg-22-749-2015. ISSN 1607-7946.
• Sparrow, Colin (1982). Lorenz-ekvationerna: bifurkationer, kaos och konstiga attraktioner . Springer.
•    Tucker, Warwick (2002). "En rigorös ODE-lösare och Smales 14:e problem" (PDF) . Grunder för beräkningsmatematik . 2 (1): 53–117. CiteSeerX 10.1.1.545.3996 . doi : 10.1007/s002080010018 . S2CID 353254 .
• Tzenov, Stephan (2014). "Konstiga attraktioner som kännetecknar den osmotiska instabiliteten". arXiv : 1406.0979v1 [ physics.flu-dyn ].
•   Viana, Marcelo (2000). "Vad är nytt på Lorenz konstiga attraktioner?". Den matematiska intelligensen . 22 (3): 6–19. doi : 10.1007/BF03025276 . S2CID 121427433 .
• Lorenz, Edward N. (1960). "Den statistiska förutsägelsen av lösningar av dynamiska ekvationer" (PDF) . Symposium om numeriska väderprognoser i Tokyo .

Vidare läsning

• GA Leonov & NV Kuznetsov (2015). "Om skillnader och likheter i analysen av Lorenz-, Chen- och Lu-system" (PDF) . Tillämpad matematik och beräkning . 256 : 334-343. doi : 10.1016/j.amc.2014.12.132 .
• Pchelintsev, AN (2022). "Om en högprecisionsmetod för att studera atttraktorer av dynamiska system och system av explosiv typ" . Matematik . 10 (8): 1207. arXiv : 2206.08195 . doi : 10.3390/math10081207 .

externa länkar

• "Lorenz attractor" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Lorenz attractor" . MathWorld .
• Lorenz attraktion av Rob Morris, Wolfram Demonstrations Project .
• Lorenz ekvation på planetmath.org
• Synkroniserat kaos och privat kommunikation, med Kevin Cuomo . Implementeringen av Lorenz-atttraktorn i en elektronisk krets.
• Lorenz attractor interaktiv animation (du behöver Adobe Shockwave-plugin)
• 3D Attractors: Mac-program för att visualisera och utforska Lorenz-atttraktorn i 3 dimensioner
• Lorenz Attractor implementerad i analog elektronisk
• Lorenz Attractor interaktiv animation (implementerad i Ada med GTK+. Källor och körbar)
• Webbaserad Lorenz Attractor (implementerad i JavaScript/HTML/CSS)
• Interaktiv webbaserad Lorenz Attractor gjord med jodid