Bifurkationsdiagram

I matematik , särskilt i dynamiska system , visar ett bifurkationsdiagram de värden som besöks eller närmade sig asymptotiskt (fixerade pekar, periodiska banor eller kaotiska attraktionsfaktorer ) av ett system som en funktion av en bifurkationsparameter i systemet. Det är vanligt att representera stabila värden med en heldragen linje och instabila värden med en prickad linje, även om de instabila punkterna ofta utelämnas. Bifurkationsdiagram möjliggör visualisering av bifurkationsteori .

Animation som visar bildandet av ett bifurkationsdiagram

Bifurkationsdiagram av cirkelkartan . Svarta områden motsvarar Arnold tungor .

Logistisk karta

Se även: Dynamiska system och Lista över kaotiska kartor

Bifurkationsdiagram av den logistiska kartan . Attraktorn värde på parametern r visas på den vertikala linjen vid den r .

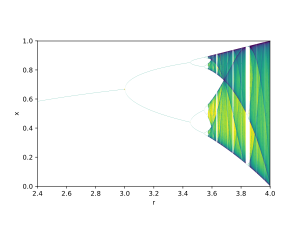
Ett exempel är bifurkationsdiagrammet för den logistiska kartan :

$x_{n+1}=rx_{n}(1-x_{n}).\,$

Bifurkationsparametern r visas på diagrammets horisontella axel och den vertikala axeln visar uppsättningen av värden för logistikfunktionen som besöks asymptotiskt från nästan alla initiala förhållanden.

Bifurkationsdiagrammet visar uppdelningen av perioderna av stabila omloppsbanor från 1 till 2 till 4 till 8 etc. Var och en av dessa bifurkationspunkter är en periodfördubblingsbifurkation . Förhållandet mellan längderna av på varandra följande intervall mellan värden på r för vilka bifurkation sker konvergerar till den första Feigenbaum-konstanten .

Diagrammet visar också periodfördubblingar från 3 till 6 till 12 etc., från 5 till 10 till 20 etc., och så vidare.

Symmetribrott i bifurkationsuppsättningar

Symmetribrott i höggaffelförgrening då parametern ε varieras. ε = 0 är fallet med symmetrisk höggaffelbifurkation.

I ett dynamiskt system som t.ex

${\ddot {x}}+f(x;\mu )+\varepsilon g(x)=0,$

som är strukturellt stabil när $\mu \neq 0$ , om ett bifurkationsdiagram plottas, behandlar $\mu$ som bifurkationsparametern, men för olika värden på $\varepsilon$ , fallet $\varepsilon =0$ är den symmetriska höggaffelbifurkationen. När $\varepsilon \neq 0$ säger vi att vi har en höggaffel med bruten symmetri. Detta illustreras i animationen till höger.

Se även

• Bifurkationsminne
• Kaosteori
• Skelett av bifurkationsdiagram
• Feigenbaums konstanter

•   Glendinning, Paul (1994). Stabilitet, instabilitet och kaos . Cambridge University Press . ISBN 0-521-41553-5 .
•    May, Robert M. (1976). "Enkla matematiska modeller med mycket komplicerad dynamik". Naturen . 261 (5560): 459–467. Bibcode : 1976 Natur.261..459M . doi : 10.1038/261459a0 . hdl : 10338.dmlcz/104555 . PMID 934280 . S2CID 2243371 .
•   Strogatz, Steven (2000). Icke-linjär dynamik och kaos: Med tillämpningar inom fysik, biologi, kemi och teknik . Perseus böcker . ISBN 0-7382-0453-6 .

externa länkar

• Den logistiska kartan och kaoset