Lode koordinater

Ytor på vilka invarianterna $\xi$ , $\rho$ , $\theta$ är konstanta. Ritad i huvudsakligt stressutrymme. Det röda planet representerar ett meridionalplan och det gula planet ett oktaedriskt plan.

Lodkoordinater $(z,r,\theta )$ eller Haigh–Westergaard-koordinater $(\xi ,\rho ,\theta )$ . är en uppsättning tensorinvarianter som spänner över utrymmet av reella , symmetriska , andra ordningens, 3-dimensionella tensorer och är isomorfa med avseende på huvudspänningsutrymme . Detta högerhänta ortogonala koordinatsystem är uppkallat för att hedra den tyske vetenskapsmannen Dr. Walter Lode på grund av hans framstående artikel skriven 1926 som beskriver effekten av den mellersta huvudspänningen på metallens plasticitet. Andra exempel på uppsättningar av tensorinvarianter är uppsättningen av huvudspänningar $(\sigma _{1},\sigma _{2},\sigma _{3})$ eller uppsättningen kinematiska invarianter $(I_{1},J_{2},J_{3})$ . Lode-koordinatsystemet kan beskrivas som ett cylindriskt koordinatsystem inom huvudspänningsutrymmet med ett sammanfallande ursprung och z-axeln parallell med vektorn ( $\displaystyle (\sigma _{1},\sigma _{2},\sigma _{3})=(1,1,1)}$ .

Mekanik invarianter

Lode-koordinaterna beräknas enklast med hjälp av mekanikinvarianter . Dessa invarianter är en blandning av invarianterna för Cauchy-spänningstensorn ${\sigma }}}$ boldsymbol och spänningsavvikaren ${\boldsymbol {s}}$ och ges av

$I_{1}=\mathrm {tr} ({\boldsymbol {\sigma }})$

$J_{2}={\frac {1}{2}}\left[{\text{tr}}({\ fetsymbol {\sigma }}^{2})-{\frac {1}{3}}{\text{tr}}({\boldsymbol {\sigma }})^{2}\right]={\frac {1}{2}}\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)={\frac {1}{2}}\lVert {\boldsymbol {s}}\rVert ^{2}$

$J_{3}=\mathrm {det} ({\boldsymbol { s}})={\frac {1}{3}}\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\cdot {\boldsymbol {s}}\right )$

som kan skrivas likvärdigt i Einstein-notation

$I_{1}=\sigma _{kk}$

$J_{2}={\frac {1}{2}}\left[{\text{tr}}({\boldsymbol {\sigma }}^{2} )-{\frac {1}{3}}{\text{tr}}({\boldsymbol {\sigma }})^{2}\right]={\frac {1}{2}}s_{ij }s_{ji}={\frac {1}{2}}s_{ij}s_{ij}$

$J_{3}={\frac {1}{6}}\epsilon _{ijk}\epsilon _{pqr}\sigma _{ip}\sigma _{jq }\sigma _{kr}={\frac {1}{3}}s_{ij}s_{jk}s_{ki}$

där $\epsilon$ är Levi-Civita-symbolen (eller permutationssymbol) och de två sista formerna för $J_{2}$ är ekvivalenta eftersom ${\boldsymbol {s}}$ är symmetrisk ( ${\displaystyle s_{ij}=s_{ji}})$ .

Gradienterna för dessa invarianter kan beräknas med

${\frac {\partial I_{1}}{\partial {\boldsymbol {\sigma }}}}={\boldsymbol {I}}$

${\frac {\partial J_{2}}{\partial {\boldsymbol {\sigma }}}}={\boldsymbol {s}}={\boldsymbol { \sigma }}-{\frac {\mathrm {tr} \left({\boldsymbol {\sigma }}\right)}{3}}{\boldsymbol {I}}$

${\frac {\partial J_{3}}{\partial {\boldsymbol {\sigma }}}}={\boldsymbol {T}}={\boldsymbol {s} }\cdot {\boldsymbol {s}}-{\frac {2J_{2}}{3}}{\boldsymbol {I}}$

där ${\boldsymbol {I}}$ är andra ordningens identitetstensor och ${\boldsymbol {T}}$ kallas Hill-tensoren.

Axiella koordinater $(z)$

z $z$ -koordinaten hittas genom att beräkna storleken på den ortogonala projektionen spänningstillståndet på den hydrostatiska axeln.

$z={\boldsymbol {E_{z}}}\colon {\boldsymbol {\sigma }}={\frac {\mathrm { tr} ({\boldsymbol {\sigma }})}{\sqrt {3}}}={\frac {I_{1}}{\sqrt {3}}}$

var

${\boldsymbol {E_{z}}}={\frac {\boldsymbol {I}}{\lVert {\boldsymbol {I}}\rVert }}={ \frac {\boldsymbol {I}}{\sqrt {3}}}$

är enhetens normal i den hydrostatiska axelns riktning.

Radiell koordinat $(r)$

r $r$ -koordinaten hittas genom att beräkna storleken på spänningsavvikaren (den ortogonala projektionen spänningstillståndet in i det deviatoriska planet).

$r={\boldsymbol {E_{r}}}\colon {\boldsymbol {\sigma }}=\lVert {\boldsymbol {s}}\ rVert ={\sqrt {2J_{2}}}$

var

${\boldsymbol {E_{r}}}={\frac {\boldsymbol {s}}{\lVert {\boldsymbol {s}}\rVert }}$

Härledning

Relationen att $r={\sqrt {2J_{2}}}$ kan hittas genom att expandera relationen $r={\frac {\boldsymbol {s}}{\lVert {\boldsymbol {s}}\rVert }}\colon {\boldsymbol {\sigma }}$ och skriva $\sigma$ i termer av de isotropa och deviatoriska delarna samtidigt som man utökar storleken på ${\boldsymbol {s}}$ $r={\frac {\boldsymbol {s}}{\sqrt {{ \boldsymbol {s}}\colon {\boldsymbol {s}}}}}\colon \left({\boldsymbol {s}}+z{\boldsymbol {E_{z}}}\right)={\frac { 1}{\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}}\left({\boldsymbol {s}}\colon {\boldsymbol {s}}+z{\boldsymbol { s}}\colon {\boldsymbol {E_{z}}}\right)$ . Eftersom ${\boldsymbol {E_{z}}}$ är isotrop och ${\boldsymbol {s}}$ är avvikande, är deras produkt noll. Vilket lämnar oss med $r={\frac {{\boldsymbol {s}}\colon {\boldsymbol {s}}}{\sqrt {{\boldsymbol {s}}\ kolon {\boldsymbol {s}}}}}={\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}$ Använder identiteten ${\boldsymbol {A}}\colon {\boldsymbol {B}}=\mathrm {tr} \left({\boldsymbol {A}} ^{T}\cdot {\boldsymbol {B}}\right)$ och med definitionen av $J_{2}={\frac {1}{2 }}\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)$ $r={\sqrt {\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)} }={\sqrt {2J_{2}}}$

är en enhetstensor i den radiella komponentens riktning.

Lode angle – vinkelkoordinat $(\theta )$

Detta diagram visar att en intuitiv approximation för Lode-vinkeln är den relativa positionen för den mellersta huvudspänningen $\lambda _{m}$ med avseende på de låga och höga huvudspänningarna.

Lode-vinkeln kan ganska löst betraktas som ett mått på belastningstyp. Lode-vinkeln varierar med avseende på mittegenvärdet för spänningen. Det finns många definitioner av Lode-vinkel som var och en använder olika trigonometriska funktioner: positiv sinus, negativ sinus och positiv cosinus (här betecknad ${\displaystyle \theta _{s}} ,$ θ $\displaystyle {\bar { \theta }}_{s}}$ , respektive ${\displaystyle \theta _{c}} )$

$\sin(3\theta _{s} )=-\sin(3{\bar {\theta}}_{s})=\cos(3\theta _{c})={\frac {J_{3}}{2}}\left({ \frac {3}{J_{2}}}\right)^{3/2}$

och är släkt med

$\theta _{s}={\frac {\pi }{6}}-\theta _{c}\qquad \qquad \theta _ {s}=-{\bar {\theta }}_{s}$

Härledning

Relationen mellan $\theta _{c}$ och $\theta _{s}$ kan visas genom att tillämpa en trigonometrisk identitet som relaterar sinus och cosinus med en förskjutning $\cos(3\theta _{c})=\sin(3\theta _{s})$ $\cos(3\theta _{c})=\sin \left(\left(3\theta _{s}-{\frac {\pi }{2}} \right)+{\frac {\pi }{2}}\right)$ $\cos(3\theta _{c} )=\cos \left(3\theta _{s}-{\frac {\pi }{2}}\right)$ . Eftersom cosinus är en jämn funktion och intervallet för den inversa cosinus vanligtvis är $0\leq \cos ^{-1}(\theta )\leq 1$ tar vi det negativa möjligt värde för termen $\theta _{s}$ , vilket säkerställer att $\theta _{c}$ är positiv. $3\theta _{c}=\pm \left(3\theta _{s}-{\frac {\pi }{2}}\right )$ $\theta _{c}={\frac {\pi}{6}}-\theta _{s}$

Dessa definitioner är alla definierade för ett intervall av $\pi /3$ .

	Spänningstillstånd $\sigma _{1}\geq \sigma _{2}\geq \sigma _{3}$	$\theta _{s}$	${\bar {\theta }}_{s}$	$\theta _{c}$
räckvidd		$-{\frac {\pi }{6}}\leq \theta _{s}\leq {\frac {\pi }{6}}$	$-{\frac {\pi }{6}}\leq \theta _{s}\leq {\frac {\pi }{6}}$	$0\leq \theta _{c}\leq {\frac {\pi }{3}}$
Triaxiell kompression (TXC)	$\sigma _{1}\geq \sigma _{2}=\sigma _{3}$	$-{\frac {\pi }{6}}$	${\frac {\pi }{6}}$	${\frac {\pi }{3}}$
Skjuvning (SHR)	$\sigma _{2}=(\sigma _{1}+\sigma _{3})/2$	$0$	$0$	${\frac {\pi }{6}}$
Triaxiell förlängning (TXE)	$\sigma _{1}=\sigma _{2}\geq \sigma _{3}$	${\frac {\pi }{6}}$	$-{\frac {\pi }{6}}$	$0$

Normalenheten i vinkelriktningen som kompletterar ortonormalbasen kan beräknas för $\theta _{s}$ och $\theta _{c}$ med hjälp av

${\boldsymbol {E_{\theta s}}}={\frac {{\boldsymbol {T}}/\lVert {\boldsymbol {T}}\rVert -\sin(3\theta _{ s}){\boldsymbol {E_{r}}}}{\cos(3\theta _{s})}}\qquad {\boldsymbol {E_{\theta c}}}={\frac {{\boldsymbol {T}}/\lVert {\boldsymbol {T}}\rVert -\cos(3\theta _{c}){\boldsymbol {E_{r}}}}{\sin(3\theta _{c} )}}$ .

Meridional profil

Denna plot visar en typisk meridional profil av flera plasticitetsmodeller: von Mises , linjär Drucker-Prager , Mohr-Coulomb , Gurson och Bigoni-Piccolroaz . Den övre delen av diagrammet skildrar flytytbeteende i triaxiell förlängning och den nedre delen skildrar flytytbeteende vid triaxiell kompression.

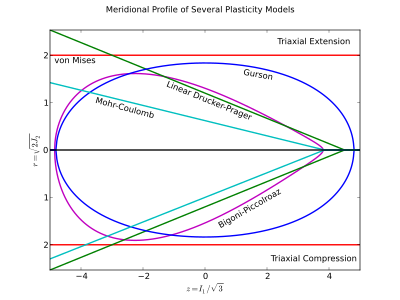
Meridionalprofilen är en 2D-plot av $(z,r)$ som håller $\theta$ konstant och plottas ibland med skalära multiplar av $z, r)}$ ( . Det används vanligtvis för att demonstrera tryckberoendet för en flytyta eller tryck-skjuvningsbanan för en spänningsbana. Eftersom $r$ är icke-negativ utelämnar plotten vanligtvis den negativa delen av $r$ -axeln, men kan inkluderas för att illustrera effekter vid motsatta Lode-vinklar (vanligtvis triaxiell förlängning och triaxiell komprimering).

En av fördelarna med att plotta meridionalprofilen med $(z,r)$ är att det är en geometriskt korrekt avbildning av flytytan. Om ett icke-isomorft par används för meridionalprofilen kommer normalen till flytytan inte att se normal ut i meridionalprofilen. Alla koordinatpar som skiljer sig från $(z,r)$ med konstanta multiplar av lika absolut värde är också isomorfa med avseende på huvudspänningsutrymmet. Som ett exempel, tryck $p=-I1/3$ och Von Mises-spänningen $\sigma _{v}={\sqrt {3J_{2 }}}$ är inte ett isomorft koordinatpar och förvränger därför avkastningsytan eftersom

$p=-{\frac {1}{\sqrt {3}}}z$

$\sigma _{v}={\sqrt {\frac {3}{2}}}r$

och slutligen $|-1/{\sqrt {3}}|\neq |{\sqrt {3/2}}|$ .

Oktaedrisk profil

Denna plot visar en typisk oktaedrisk profil av flera plasticitetsmodeller: von Mises , linjär Drucker-Prager , Mohr-Coulomb , Gurson och Bigoni-Piccolroaz . Denna plot har utelämnat Lode-vinkelvärden till förmån för laddningsbeskrivningar på grund av övervikten av definitioner av Lode-vinkeln. Den radiella koordinaten är $r={\sqrt {2J_{2}}}$ .

Den oktaedriska profilen är en 2D-plot av $(r,\theta )$ som håller $z$ konstant. Att plotta flytytan i det oktaedriska planet visar nivån av Lode-vinkelberoende. Det oktaedriska planet kallas ibland för "pi-planet" eller "deviatoriskt plan".

Den oktaedriska profilen är inte nödvändigtvis konstant för olika tryckvärden med de anmärkningsvärda undantagen från von Mises flytningskriteriet och Tresca flytningskriteriet som är konstanta för alla tryckvärden.

En anteckning om terminologi

Termen Haigh-Westergaard-rymden används tvetydigt i litteraturen för att betyda både det kartesiska huvudspänningsutrymmet och det cylindriska Lode-koordinatutrymmet

Se även

• Yield (teknik)
• Plasticitet (fysik)
• Påfrestning
• Henri Tresca
• von Mises stressar
• Mohr-Coulombs teori
• Anstränga
• Spänn tensor
• Stress-energitensor
• Stresskoncentration
• 3-D elasticitet