Lista över tröghetsmoment

Tröghetsmoment , betecknat med I , mäter i vilken utsträckning ett objekt motstår rotationsacceleration kring en viss axel , det är rotationsanalogen till massa (som bestämmer ett objekts motstånd mot linjär acceleration ). En massas tröghetsmoment har måttenheter ML 2 ⁽ [massa] × [längd] ² ) . Det ska inte förväxlas med områdets andra ögonblick , som används i strålberäkningar. Masströghetsmomentet är ofta också känt som rotationströgheten , och ibland som vinkelmassan .

För enkla objekt med geometrisk symmetri kan man ofta bestämma tröghetsmomentet i ett exakt sluten form uttryck . Vanligtvis inträffar detta när masstätheten är konstant, men i vissa fall kan densiteten också variera genom objektet. I allmänhet är det kanske inte helt enkelt att symboliskt uttrycka tröghetsmomentet för former med mer komplicerade massfördelningar och som saknar symmetri. När man beräknar tröghetsmoment är det användbart att komma ihåg att det är en additiv funktion och utnyttja parallellaxelns och vinkelräta axelsatser .

Den här artikeln tar huvudsakligen hänsyn till symmetriska massfördelningar, med konstant densitet genom hela objektet, och rotationsaxeln antas vara genom masscentrum om inte annat anges.

Tröghetsmoment

Följande är skalära tröghetsmoment. I allmänhet är tröghetsmomentet en tensor , se nedan.

Beskrivning	Figur	Tröghetsmoment
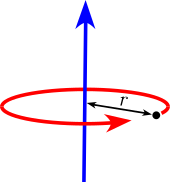
Peka massan M på ett avstånd r från rotationsaxeln. En punktmassa har inte ett tröghetsmoment runt sin egen axel, men med hjälp av parallellaxelsatsen uppnås ett tröghetsmoment runt en avlägsen rotationsaxel.		$I=Mr^{2}$
Två punktmassor, m 1 och m 2 , med reducerad massa μ och åtskilda av ett avstånd x , runt en axel som går genom systemets masscentrum och vinkelrätt mot linjen som förbinder de två partiklarna.		$I={\frac {m_{1}m_{2}}{m_{1}\!+\!m_{2}} }x^{2}=\mu x^{2}$
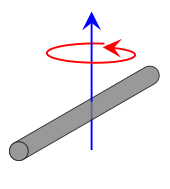
Tunn stång med längden L och massan m , vinkelrät mot rotationsaxeln, roterande kring dess centrum. Detta uttryck förutsätter att staven är en oändligt tunn (men stel) tråd. Detta är ett specialfall av den tunna rektangulära plattan med rotationsaxel i mitten av plattan, med w = L och h = 0.		$I_{\mathrm {center} }={\frac {1}{12}}mL^{2}\,\!$
Tunn stång med längden L och massan m , vinkelrät mot rotationsaxeln, roterande runt ena änden. Detta uttryck förutsätter att staven är en oändligt tunn (men stel) tråd. Detta är också ett specialfall av den tunna rektangulära plattan med rotationsaxel i slutet av plattan, med h = L och w = 0.		$I_{\mathrm {end} }={\frac {1}{3}}mL^{2}\,\!$
Tunn cirkulär slinga med radie r och massa m . Detta är ett specialfall av en torus för a = 0 (se nedan), såväl som av ett tjockväggigt cylindriskt rör med öppna ändar, med r 1 = r 2 och h = 0.		$I_{z}=mr^{2}\!$$I_{x}=I_{y}={\frac { 1}{2}}mr^{2}\,\!$
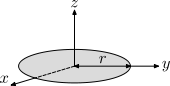
Tunn, solid skiva med radie r och massa m . Detta är ett specialfall av den solida cylindern, med h = 0. Att $I_{x}=I_{y}={\frac {I_{z}}{2} }\,$ är en konsekvens av den vinkelräta axelsatsen .		$I_{z}={\frac {1}{2}}mr^{2}\,\!$$I_{x}=I_{y}={\frac {1}{4}}mr^{2}\,\!$
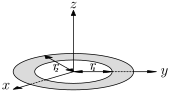
En enhetlig ring (skiva med ett koncentriskt hål) med massan m , inre radie r 1 och yttre radie r 2		$I_{z}={\frac {1}{2}}m(r_{1}^{2}+r_{2}^{ 2})$ $I_{x}=I_{y}={\frac {1}{4}}m(r_{1}^{2 }+r_{2}^{2})$
En ring med konstant areadensitet $\rho _{A}$		$I_{z}={\frac {1}{2}}\pi \rho _{A}(r_{2}^{ 4}-r_{1}^{4})$ $I_{x}=I_{y}={\frac {1}{4}}\pi \rho _{A }(r_{2}^{4}-r_{1}^{4})$
Tunt cylindriskt skal med öppna ändar, med radie r och massa m . Detta uttryck förutsätter att skaltjockleken är försumbar. Det är ett specialfall av det tjockväggiga cylindriska röret för r 1 = r 2 . Dessutom har en punktmassa m i slutet av en stav med längden r samma tröghetsmoment och värdet r kallas svängningsradien .		$I\approx mr^{2}\,\!$
Massiv cylinder med radie r , höjd h och massa m . Detta är ett specialfall av det tjockväggiga cylindriska röret, med r 1 = 0.		$I_{z}={\frac {1}{2}}mr^{2}\,\!$$I_{x}=I_{y}={\frac {1}{12}}m\left(3r^{2}+h^{2}\right)$
Tjockväggigt cylindriskt rör med öppna ändar, med inre radie r 1 , yttre radie r 2 , längd h och massa m .		$I_{z}={\frac {1}{2}}m\left (r_{2}^{2}+r_{1}^{2}\right)=mr_{2}^{2}\left(1-t+{\frac {t^{2}}{2}} \right)$ där t = ( r 2 − r 1 )/ r 2 är ett normaliserat tjockleksförhållande; $I_{x}=I_{y}={\frac {1}{12}}m\left (3\left(r_{2}^{2}+r_{1}^{2}\right)+h^{2}\right)$ Formeln ovan är för xy-planet som passerar genom masscentrum, som sammanfaller med cylinderns geometriska centrum. Om xy-planet är vid basen av cylindern, dvs förskjutet med $d={\frac {h}{2}},$ då gäller vid parallellaxelsatsen följande formel: $I_{x}=I_{y}={\frac {1}{12}}m\left(3\left(r_{2}^{2}+r_{1}^{2 }\right)+4h^{2}\right)$
Med en densitet på ρ och samma geometri		$I_{z}={\frac {\pi \rho h}{2}}\left(r_{2}^{4}- r_{1}^{4}\right)$ $I_{x}=I_{y}={\frac {\pi \rho h}{12}}\left(3(r_{2}^{4}-r_{1}^{4})+h^{2}(r_{2}^{2}- r_{1}^{2})\right)$
Regelbunden tetraeder av sidan s och massa m		$I_{\mathrm {solid} }={\frac {1}{20}}ms^{2}\,\!$ $I_{\mathrm {hollow} }={\frac {1}{12}}ms^{2}\,\!$
Regelbunden oktaeder på sidan s och massa m		$I_{x,\mathrm {hollow} }=I_ {y,\mathrm {hollow} }=I_{z,\mathrm {hollow} }={\frac {1}{6}}ms^{2}\,\!$$I_{x,\mathrm {solid} }=I_{y,\mathrm {solid} }=I_{ z,\mathrm {solid} }={\frac {1}{10}}ms^{2}\,\!$
Regelbunden dodekaeder av sidan s och massa m		$I_{x,\mathrm {hollow} }=I_{y,\mathrm {hollow} }=I_{z,\mathrm {hollow} }={\frac {39\phi +28}{90}}ms^{2}$ ${\displaystyle I_{x,\mathrm {solid} }=I_ {y,\mathrm {solid} }=I_{z,\mathrm {solid} }={\frac {39\phi +28}{150}}ms^{2}\,\!} ($ där $\phi ={\frac {1+{\sqrt {5}}}{2}}$ )
Vanlig ikosaeder av sid s och massa m		$I_{x,\mathrm {hollow} }= I_{y,\mathrm {hollow} }=I_{z,\mathrm {hollow} }={\frac {\phi ^{2}}{6}}ms^{2}$ $I_{x,\mathrm {solid} }=I_{y ,\mathrm {solid} }=I_{z,\mathrm {solid} }={\frac {\phi ^{2}}{10}}ms^{2}\,\!$
Ihålig sfär med radie r och massa m .		$I={\frac {2}{3}}mr^{2}\,\!$
Solid sfär (kula) med radie r och massa m .		$I={\frac {2}{5}}mr^{2}\,\!$
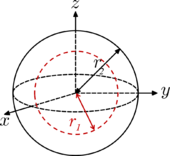
Sfär (skal) med radie r 2 och massa m , med centrerad sfärisk hålighet med radie r 1 . När kavitetsradien r 1 = 0 är föremålet en solid boll (ovan). När r 1 = r 2 , ${\frac {r_{2}^{5}-r_{1}^{5 }}{r_{2}^{3}-r_{1}^{3}}}={\frac {5}{3}}r_{2}^{2}$ och objektet är en ihålig sfär .		$I={\frac {2}{5}}m\cdot {\frac {r_{2}^{5} -r_{1}^{5}}{r_{2}^{3}-r_{1}^{3}}}\,\!$
Rätt cirkulär kon med radie r , höjd h och massa m		$I_{z}={\frac {3}{10}}mr^{2}\,\!$      Om en axel som går genom spetsen: $I_{x}=I_{y}=m\left({\frac {3}{ 20}}r^{2}+{\frac {3}{5}}h^{2}\right)\,\!$ Om en axel som går genom basen: $I_{x}=I_{y}=m\left({\frac {3}{20}}r^{2}+{\frac {1}{10}}h^{2}\right )\,\!$ Om en axel som går genom massans centrum: $I_{x}=I_{y}=m\left ({\frac {3}{20}}r^{2}+{\frac {3}{80}}h^{2}\right)\,\!$
Rätt cirkulär ihålig kon med radie r , höjd h och massa m		$I_{z}={\frac {1}{2}}mr^{2}\,\!$$I_{x}=I_{y}={\frac {1}{4}}m\left(r^{2}+2h^{2}\right)\,\!$
Torus med mindre radie a , större radie b och massa m .		Om en axel som går genom mitten och vinkelrät mot diametern: ${\frac {1}{4}}m\left(4b^{2}+3a^ {2}\right)$ Ungefär en diameter: ${\frac {1}{8}}m\left(5a^{2}+4b^{2 }\höger)$
Ellipsoid (fast form) av halvaxlarna a , b , och c med massan m		$I_{a}={\frac {1}{5}}m\left(b^{2}+c^{2}\right)\ ,\!$$I_{b}={\frac {1}{5}}m\left(a^{2}+c^{2} \right)\,\!$$I_{c}={\frac {1}{5}}m\left(a^{2}+b^{2}\right)\,\!$
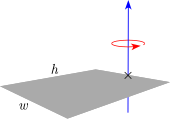
Tunn rektangulär platta med höjd h , bredd w och massa m (rotationsaxel vid plattans ände)		$I_{e}={\frac {1}{12}}m\left(4h^{2}+w^{2}\right) \,\!$
Tunn rektangulär platta med höjd h , bredd w och massa m (rotationsaxel i mitten)		$I_{c}={\frac {1}{12}}m\left(h^{2}+w^{2}\right)\ ,\!$
Tunn rektangulär platta med massan m, längden på sidan som gränsar till sidan som innehåller rotationsaxeln är r (rotationsaxel längs en sida av plattan)		$I={\frac {1}{3}}mr^{2}$
Massiv kub med höjd h , bredd w , och djup d , och massa m . För en liknande orienterad kub med sidor av längden $s$ , $I_{\mathrm {CM} }={\frac {1}{6}}ms^{ 2}\,\!$		$I_{h}={\frac {1}{12}}m\left(w^{2}+d^{2}\right)$$I_{w}={\frac {1}{12}}m\left(d^{2}+h^{2}\right)$$I_{d}={\frac {1}{12}}m\left(w^{2}+h^{2}\right)$
Massiv kub med höjd D , bredd W och längd L , och massa m , roterande kring den längsta diagonalen. För en kub med sidorna $s$ , $I={\frac {1}{6}}ms^{2}\,\!$ .		$I={\frac {1}{6}}m\left({\ frac {W^{2}D^{2}+D^{2}L^{2}+W^{2}L^{2}}{W^{2}+D^{2}+L^ {2}}}\right)$
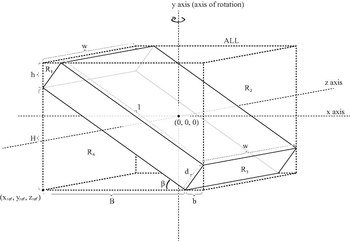
Lutad massiv kub med djup d , bredd w och längd l och massa m , roterande runt den vertikala axeln (y-axeln som ses i figuren). För en kub med sidorna $s$ , $I={\frac {1}{6}}ms^{2}\,\!$ .		$I={\frac {m}{12}}\left(l^{2}\cos ^{2 }\beta +d^{2}\sin ^{2}\beta +w^{2}\right)$
Triangel med hörn i origo och vid P och Q , med massa m , roterande runt en axel vinkelrät mot planet och passerar genom origo.		$I={\frac {1}{6}}m(\mathbf {P} \cdot \mathbf {P} +\mathbf {P} \cdot \mathbf {Q} +\mathbf {Q} \cdot \mathbf {Q} )$
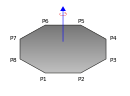
Plan polygon med hörn P 1 , P 2 , P 3 , ..., P N och massa m likformigt fördelade på sitt inre, roterande runt en axel vinkelrät mot planet och passerar genom origo.		$I=m\left({\frac {\sum \limits _{n=1}^{N}\|\mathbf {P} _{n+ 1}\times \mathbf {P} _{n}\|\left(\left(\mathbf {P} _{n}\cdot \mathbf {P} _{n}\right)+\left(\mathbf {P} _{n}\cdot \mathbf {P} _{n+1}\right)+\left(\mathbf {P} _{n+1}\cdot \mathbf {P} _{n+1 }\right)\right)}{6\sum \limits _{n=1}^{N}\|\mathbf {P} _{n+1}\times \mathbf {P} _{n}\| }}\höger)$
Plan regelbunden polygon med n -hörn och massa m likformigt fördelade på dess inre, roterande kring en axel vinkelrät mot planet och passerar genom dess barycenter . R är radien för den omskrivna cirkeln .		$I={\frac {1}{2}}mR^{2}\left(1-{\frac {2 }{3}}\sin ^{2}\left({\tfrac {\pi }{n}}\right)\right)$
En likbent triangel med massan M , vertexvinkeln 2β och den gemensamma sidans längd L (axel genom spets, vinkelrät mot planet)		$I={\frac {1}{2}}mL^{2}\left(1-{\frac {2} {3}}\sin ^{2}\left(\beta \right)\right)$
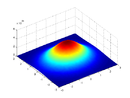
Oändlig skiva med massa fördelad i en tvåvariabel Gauss-fördelning på två axlar runt rotationsaxeln med massdensitet som funktion av positionsvektorn ${\mathbf {x} }$ $\rho ({\mathbf {x} })=m{\frac {\exp \left(-{\frac {1}{2}}{\mathbf {x} }^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}{\mathbf {x} }\right)}{\sqrt {(2\pi )^{2}|{\boldsymbol {\Sigma }}|}} }$		$I=m\cdot \operatörsnamn {tr} ({\boldsymbol {\Sigma }})\,\!$

Lista över 3D-tröghetstensorer

Denna lista över tröghetsmomenttensorer ges för huvudaxlar för varje objekt.

För att erhålla de skalära tröghetsmomenten I ovan projiceras tensortröghetsmomentet I längs någon axel definierad av en enhetsvektor n enligt formeln:

$\mathbf {n} \cdot \mathbf {I} \cdot \mathbf {n} \equiv n_{i}I_{ij}n_{j} \,,$

där prickarna indikerar tensorkontraktion och Einsteins summationskonvention används. I tabellen ovan n vara den kartesiska enheten e _x , e _y , e _z för att erhålla I _x , I _y , I _z respektive.

Beskrivning	Figur	Tröghetsmoment tensor
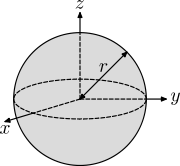
Fast sfär med radie r och massa m		$I={\begin{bmatrix}{\frac {2}{5}}mr^{2}&0&0\\0&{ \frac {2}{5}}mr^{2}&0\\0&0&{\frac {2}{5}}mr^{2}\end{bmatrix}}$
Ihålig sfär med radie r och massa m		$I={\begin{bmatrix}{\frac {2}{3}}mr^{2}&0&0\\0&{ \frac {2}{3}}mr^{2}&0\\0&0&{\frac {2}{3}}mr^{2}\end{bmatrix}}$
Solid ellipsoid av halvaxlar a , b , c och massa m		$I={\begin{bmatrix}{\frac {1 }{5}}m(b^{2}+c^{2})&0&0\\0&{\frac {1}{5}}m(a^{2}+c^{2})&0\\ 0&0&{\frac {1}{5}}m(a^{2}+b^{2})\end{bmatrix}}$
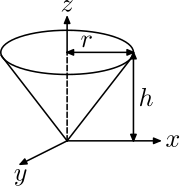
Rätt cirkulär kon med radie r , höjd h och massa m , omkring spetsen		$I={\begin{bmatrix}{\frac {3}{5 }}mh^{2}+{\frac {3}{20}}mr^{2}&0&0\\0&{\frac {3}{5}}mh^{2}+{\frac {3}{ 20}}mr^{2}&0\\0&0&{\frac {3}{10}}mr^{2}\end{bmatrix}}$
Massiv kub med bredd w , höjd h , djup d och massa m		$I={\begin{bmatrix}{\frac {1 }{12}}m(h^{2}+d^{2})&0&0\\0&{\frac {1}{12}}m(w^{2}+d^{2})&0\\ 0&0&{\frac {1}{12}}m(w^{2}+h^{2})\end{bmatrix}}$
Smal stång längs y -axeln med längden l och massan m runt änden		$I={\begin{bmatrix}{\frac {1}{3}}ml^{2}&0&0\\0&0&0\\0&0&{\frac {1}{3}}ml^{2}\end{bmatrix}}$
Smal stång längs y -axeln med längden l och massan m omkring mitten		$I={\begin{bmatrix}{\frac {1}{12}}ml^{2}&0&0\\0&0&0\\0&0&{\frac {1}{12}}ml^{2}\end{bmatrix}}$
Massiv cylinder med radie r , höjd h och massa m		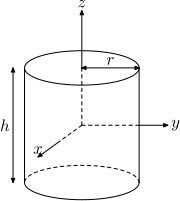$I={\begin{bmatrix}{\frac {1}{12 }}m(3r^{2}+h^{2})&0&0\\0&{\frac {1}{12}}m(3r^{2}+h^{2})&0\\0&0&{\ frac {1}{2}}mr^{2}\end{bmatrix}}$
Tjockväggigt cylindriskt rör med öppna ändar, med inre radie r 1 , yttre radie r 2 , längd h och massa m		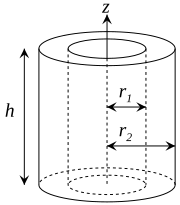$I={\begin{bmatrix}{\frac {1}{12}}m(3(r_{2}^{2}+r_{1}^{2})+h^{2}) &0&0\\0&{\frac {1}{12}}m(3(r_{2}^{2}+r_{1}^{2})+h^{2})&0\\0&0&{\frac {1}{2}}m(r_{2}^{2}+r_{1}^{2})\end{bmatrix}}$

Se även

• Lista över andra ögonblick av området
• Parallellaxelsats
• Perpendikulär axelsats

externa länkar

• Tröghetstensorn hos en tetraeder
• Handledning om att härleda tröghetsmoment för vanliga former