Laguerre plan

Inom matematiken är ett Laguerre-plan en av de tre typerna av Benz-plan , som är Möbius-planet , Laguerre-planet och Minkowski-planet . Laguerre-plan är uppkallade efter den franske matematikern Edmond Nicolas Laguerre .

klassiskt Laguerre-plan: 2d/3d-modell

Det klassiska Laguerre-planet är en infallsstruktur som beskriver infallsbeteendet för kurvorna ${\displaystyle y=ax^{2}+bx+c} ,$ dvs paraboler och linjer, i den verkliga affint plan . För att förenkla strukturen, till valfri kurva $y=ax^{2}+bx+c$$(\infty ,a )$ ( läggs till. En ytterligare fördel med denna komplettering är att plangeometrin för de färdiga parabolerna/linjerna är isomorf med geometrin för de plana sektionerna av en cylinder (se nedan).

Det klassiska riktiga Laguerre-planet

Ursprungligen definierades det klassiska Laguerre-planet som geometrin för de orienterade linjerna och cirklarna i det verkliga euklidiska planet (se ). Här föredrar vi parabelmodellen av det klassiska Laguerre-planet.

Vi definierar:

${\mathcal {P}}:=\mathbb {R} ^{2}\cup (\{\infty \}\times \mathbb {R} ),\ \infty \notin \mathbb {R} ,$ uppsättningen av punkter , ${\mathcal {Z}}:=\{\{(x,y)\in \mathbb {R} ^{2}\mid y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\mid a,b,c\in \mathbb {R} \}$ uppsättningen cykler .

Incidensstrukturen $({\mathcal {P}},{\mathcal {Z}},\in )$ kallas klassisk Laguerre-plan .

Punktmängden är $\mathbb {R} ^{2}$ plus en kopia av $\mathbb {R}$ (se figur). Vilken parabel/linje som helst $y=ax^{2}+bx+c$ får den extra punkten $(\infty ,a)$ .

Punkter med samma x-koordinat kan inte kopplas samman med kurvorna $y=ax^{2}+bx+c$ . Därför definierar vi:

Två punkter $A,B$ är parallella ( $A\parallel B$ ) om $A=B$ eller om det inte finns någon cykel som innehåller $A$ och $B$ .

För beskrivningen av det klassiska verkliga Laguerre-planet ovanför två punkter $(a_{1},a_{2}),(b_{1},b_{ 2})$ är parallella om och endast om $a_{1}=b_{1}$ . $\parallel$ är en ekvivalensrelation , liknande linjers parallellitet.

Incidensstrukturen $({\mathcal {P}},{\mathcal {Z}},\in )$ har följande egenskaper:

Lemma:

• För alla tre punkter $A,B,C$ , parvis inte parallella, finns det exakt en cykel $z$ som innehåller ${\displaystyle A,B,C$ .
• För vilken punkt ${\displaystyle P} som helst$ och varje cykel $z$ finns det exakt en punkt $P'\in z$ så att $P\parallel P'$ .
• För varje cykel $z$ , vilken punkt ${\displaystyle P\in z} som helst$ och vilken punkt $Q\notin z$ som helst som inte är parallell med $P$ finns det exakt en cykel $z'$ till $P,Q$ med $z\cap z'=\{P\}$ , dvs. ${ \displaystyle z}$ och $z'$ berör varandra vid $P$ .

Laguerre-plan: stereografisk projektion av xz-planet på en cylinder

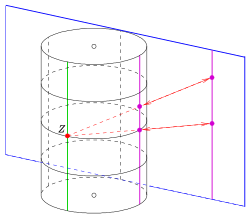
I likhet med sfärmodellen för det klassiska Moebius-planet finns det en cylindermodell för det klassiska Laguerre-planet:

$({\mathcal {P}},{\mathcal {Z}},\in )$ är isomorft till geometrin för plana sektioner av en cirkulär cylinder i $\ mathbb {R} ^{3}$ .

Följande mappning $\Phi$ är en projektion med centrum $(0,1,0)$ som mappar xz-planet på cylindern med ekvationen $u^{2}+v^{2}-v=0$ , axel $(0,{\tfrac {1}{2}},..)$ och radie $r={\tfrac {1}{2}}\ :$

$\Phi :\ (x,z)\högerpil ({\frac {x}{1+x^{2}}},{\frac {x^{2}}{1+x^{2} }},{\frac {z}{1+x^{2}}})=(u,v,w)\ .$

• Punkterna $(0,1,a)$ (linje på cylindern genom mitten) visas inte som bilder.
• $\Phi$ projicerar parabeln/linjen med ekvation $z=ax^{2}+bx+c$ i planet $wa=bu+(ac)(v-1)$ . Så, bilden av parabeln/linjen är den plana delen av cylindern med ett icke vinkelrät plan och därmed en cirkel/ellips utan punkt ( , $displaystyle (0,1,a)}$ . Parabolerna/linjen $z=ax^{2}+a$ är mappade på (horisontella) cirklar.
• En linje(a=0) avbildas på en cirkel/ellips genom centrum $(0,1,0)$ och en parabel ( $a\neq 0$ ) på en cirkel /ellips som inte innehåller $(0,1,0)$ .

Axiomen för ett Laguerre-plan

Lemmat ovan ger upphov till följande definition:

Låt ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )} vara$ en incidensstruktur med punkt ställ in ${\mathcal {P}}$ och uppsättning cykler ${\mathcal {Z}}$ . Två punkter $A,B$ är parallella ( $A\parallel B$ ) om $A=B$ eller om det inte finns någon cykel som innehåller $A$ och $B$ . ${\mathcal {L}}$ kallas Laguerre-plan om följande axiom gäller:

Laguerre-planet: axiom

B1: För alla tre punkter ${\displaystyle A,B,C} , parvis inte$$A,B, C$ , finns det exakt en cykel $z$ som innehåller .

B2: För valfri punkt $P$ och valfri cykel $z$ finns det exakt en punkt $P'\in z$ så att $P\parallel P'$ .

B3: För valfri cykel $z$ , valfri punkt $P\in z$ och valfri punkt $Q\notin z$ som inte är parallell med $P$ det finns exakt en cykel $z'$ genom $P,Q$ med $z\cap z'=\{P\}$ ,

dvs. $z$ och $z'$ berör varandra vid $P$ .

B4: Varje cykel innehåller minst tre punkter. Det finns minst en cykel. Det finns minst fyra punkter som inte är på en cykel.

Fyra punkter $A,B,C,D$ är koncykliska om det finns en cykel $z$ med $A,B, C,D\in z$ .

Från definitionen av relation $\parallel$ och axiom B2 får vi

Lemma: Relation $\parallel$ är en ekvivalensrelation .

Efter cylindermodellen av det klassiska Laguerre-planet introducerar vi beteckningen:

a) För $P\in {\mathcal {P}}$ sätter vi ${\overline {P}}:=\{Q\in {\mathcal {P}}\ |\ P\parallel Q\}$ . b) En ekvivalensklass ${\overline {P}}$ kallas generator .

För det klassiska Laguerre-planet är en generator en linje parallell med y-axeln (planmodell) eller en linje på cylindern (rymdmodell).

Kopplingen till linjär geometri ges av följande definition:

För ett Laguerre-plan ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )} definierar$ vi lokal struktur

${\mathcal {A }}_{P}:=({\mathcal {P}}\setminus \{{\overline {P}}\},\{z\setminus \{{\overline {P}}\}\ |\ P \in z\in {\mathcal {Z}}\}\cup \{{\overline {Q}}\ |\ Q\in {\mathcal {P}}\setminus \{{\overline {P}}\ },\i )$

och kalla det resten vid punkt P.

I planmodellen av det klassiska Laguerre-planet är ${\mathcal {A}}_{\infty }$ det verkliga affina planet $\mathbb {R} ^{2}$ . I allmänhet får vi

Sats: Varje rest av ett Laguerre-plan är ett affint plan .

Och motsvarande definition av ett Laguerre-plan:

Sats: En incidensstruktur tillsammans med en ekvivalensrelation $\parallel$ på ${\mathcal {P}}$ är ett Laguerre-plan om och endast om för någon punkt $P$ är resten ${\mathcal {A}}_{P}$ är ett affint plan.

Finita Laguerre-plan

minimal modell av ett Laguerre-plan (endast 4 av 8 cykler visas)

Följande infallsstruktur är en "minimal modell" av ett Laguerre-plan:

${\mathcal {P}}:=\{A_{1},A_{2},B_{1 },B_{2},C_{1},C_{2}\}\ ,$

${\mathcal {Z}}:=\{\{A_{i},B_{j},C_{k}\}\ |\ i,j, k=1,2\}\ ,$

$A_{1}\parallel A_{2},\ B_{1}\parallel B_{2},\ C_{1}\parallel C_{2}\ .$

Därför $|{\mathcal {P}}|=6$ och $|{\mathcal {Z}}|=8\ .$

För finita Laguerre-plan, dvs $|{\mathcal {P}}|<\infty$ , vi får:

Lemma: För alla cykler $z_{1},z_{2}$ och valfri generator ${\overline {P}}$ av ett ändligt Laguerre-plan ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )} vi har$ :

$|z_{1}|=|z_{2}|=|{\overline {P}}|+1$ .

För ett ändligt Laguerre-plan ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )} och$ en cykel $z\in {\mathcal {Z}}$ heltal $n:=|z|-1$ kallas ordningen för ${\mathcal {L}}$ .

Från kombinatorik får vi

Lemma: Låt ${\displaystyle {\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )} vara en$ Laguerre— ordningsplan $n$ . Sedan

a) eventuell rest ${\mathcal {A}}_{P}$ är ett affint plan av ordningen $n\quad ,$ b) $|{\mathcal {P}}|=n^{2}+n,$ c) $|{\mathcal {Z}}|=n^{3}.$

Miquelian Laguerre-plan

Till skillnad från Moebius-plan leder den formella generaliseringen av den klassiska modellen av ett Laguerre-plan, dvs att ersätta $\mathbb {R}$ med ett godtyckligt fält ${\displaystyle K} ,$ alltid till ett exempel på ett Laguerre-plan.

Sats: För ett fält $K$ och

${\mathcal {P}}:=K^{2}\cup$$(\{\infty \}\times K ),\ \infty \notin K$ ,

${\displaystyle {\mathcal {Z}}:=\{\{(x,y)\in K^{2}\ |\ y=ax^{2}+bx+c \}\cup \{(\infty ,a)\}\ |\ a,b,c\in K\}} incidensstrukturen$ L

${\displaystyle {\mathcal {L}}(K):=({\mathcal {P}},{\mathcal {Z}},\in )} är$ ett Laguerre-plan med följande parallellförhållande: $(a_{1},a_{2})\parallel (b_{1},b_{2})$ om och endast om $a_{1}= b_{1}$ .

På samma sätt som ett Möbius-plan har Laguerre-versionen av Miquels sats:

Miquels sats (cirklar ritade istället för paraboler)

Miquels sats: För Laguerre-planet ${\mathcal {L}}(K)$ gäller följande:

Om för några 8 parvisa inte parallella punkter $P_{1},\ldots ,P_{8}$ som kan tilldelas till hörnen på en kub så att punkterna i 5 ytor motsvarar koncykliska fyrdubblar så är den sjätte fyrdubblingen av poäng också koncyklisk.

(För en bättre översikt i figuren finns cirklar ritade istället för paraboler)

Vikten av Miquels sats framgår av följande sats, som beror på vd Waerden, Smid och Chen:

Sats: Endast ett Laguerre-plan ${\mathcal {L}}(K)$ uppfyller Miquels sats.

På grund av den sista satsen ${\displaystyle {\mathcal {L}}(K)} ett "Miquelian Laguerre-plan".$ kallas

Den minimala modellen av ett Laguerre-plan är miquelian. Det är isomorft till Laguerre-planet ${\mathcal {L}}(K)$ med $K=GF(2)$ (fält ${ \displaystyle \{0,1\}}$ ).

En lämplig stereografisk projektion visar att ${\mathcal {L}}(K)$ är isomorf till geometrin för de plana sektionerna på en fyrcylinder över fältet $K$ .

Ovoidala Laguerre-plan

Det finns många Laguerre-plan som inte är miquelian (se webblänk nedan). Den klass som mest liknar miquelian Laguerre-plan är de äggformade Laguerre-planen . Ett äggformigt Laguerre-plan är geometrin hos de plana sektionerna av en cylinder som är konstruerad genom att använda en oval istället för en icke degenererad kon. En oval är en kvadratisk mängd och har samma geometriska egenskaper som en icke degenererad kon i ett projektivt plan: 1) en linje skär en oval i noll, en eller två punkter och 2) vid vilken punkt som helst finns det en unik tangent. En enkel oval i det verkliga planet kan konstrueras genom att limma ihop två lämpliga halvor av olika ellipser, så att resultatet inte blir en konisk. Även i det finita fallet finns det ovaler (se kvadratisk mängd ) .

Se även

• Laguerre-förvandlingar

externa länkar

• Benz plan i Encyclopedia of Mathematics
• Föreläsningsanteckning Planar Circle Geometries , an Introduction to Moebius-, Laguerre- och Minkowski Planes, s. 67