Benz plan

I matematik är ett Benz-plan en typ av 2- dimensionell geometrisk struktur, uppkallad efter den tyske matematikern Walter Benz . Termen applicerades på en grupp objekt som uppstår från en gemensam axiomatisering av vissa strukturer och delas upp i tre familjer, som introducerades separat: Möbiusplan , Laguerreplan och Minkowskiplan .

Möbius plan

Klassiskt Möbius-plan: 2d/3d-modell

Att utgå från det verkliga euklidiska planet och slå samman uppsättningen av linjer med uppsättningen cirklar för att bilda en uppsättning block resulterar i en inhomogen infallsstruktur : tre distinkta punkter bestämmer ett block, men linjer kan särskiljas som en uppsättning block som parvis skär varandra vid en punkt utan att vara tangent (eller inga punkter när de är parallella). Att lägga till den nya punkten $\infty$ , definierad för att ligga på varje linje resulterar i att varje block bestäms av exakt tre punkter, såväl som skärningspunkten mellan två block som följer ett enhetligt mönster (skärning vid två punkter, tangerande eller icke-korsande). Denna homogena geometri kallas klassisk inversiv geometri eller ett Möbiusplan. Inhomogeniteten i beskrivningen (linjer, cirklar, ny punkt) kan ses vara icke-substantiv genom att använda en 3-dimensionell modell. Genom att använda en stereografisk projektion kan det klassiska Möbius-planet ses vara isomorft till geometrin för plana sektioner (cirklar) på en sfär i euklidiskt 3-rum.

Analogt med det (axiomatiska) projektiva planet definierar ett (axiomatiskt) Möbius-plan en infallsstruktur. Möbiusplan kan på liknande sätt konstrueras över fält än de reella talen.

Laguerre plan

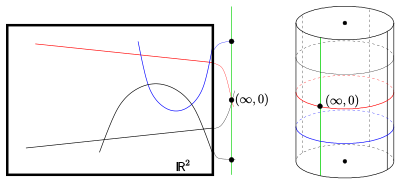
klassiskt Laguerre-plan: 2d/3d-modell

Börjar om från $\textstyle \mathbb {R} ^{2}$ och tar kurvorna med ekvationerna $y=ax^{2}+bx+c$ (paraboler och linjer) som block, är följande homogenisering effektiv: Lägg till kurvan $y=ax^{2}+bx+c$ den nya punkten $(\infty ,a)$ . Därför är uppsättningen av punkter $(\mathbb {R} \cup {\infty })\times \mathbb {R}$ . Denna geometri av paraboler kallas det klassiska Laguerre-planet (ursprungligen designades det som geometrin för de orienterade linjerna och cirklarna. Båda geometrierna är isomorfa.)

När det gäller Möbius-planet finns det en 3-dimensionell modell: geometrin för de elliptiska plansektionerna på en ortogonal cylinder (i ${\displaystyle \mathbb {R} ^{3}} )$ . En abstraktion leder (analogt till Möbius-planet) till det axiomatiska Laguerre-planet.

Minkowski-plan

klassiskt Minkowski-plan: 2d/3d-modell

Börja från $\mathbb {R} ^{2}$ och slå samman linjerna $y=mx+d,m\neq 0$ med hyperbolerna $y={\tfrac {a}{xb}}+c,a\neq 0$ för att få uppsättningen av block, homogeniserar följande idé incidensstrukturen: Lägg till vilken linje som helst punkten $(\infty ,\infty )$ och till valfri hyperbel $y={\tfrac {a}{xb}} +c,a\neq 0$ de två punkterna $(b,\infty ),(\infty ,c)$ . Därför är punktmängden $(\mathbb {R} \cup \{\infty \})^{2}$ . Denna geometri hos hyperbolerna kallas det klassiska Minkowski-planet.

Analogt med de klassiska Möbius- och Laguerre-planen finns det en 3-dimensionell modell: Det klassiska Minkowski-planet är isomorft med geometrin för plana sektioner av en hyperboloid av ett ark (icke-degenererad kvadrisk av index 2) i 3-dimensionell projektiv rymd . I likhet med de två första fallen får vi det (axiomatiska) Minkowski-planet.

Plana cirkelgeometrier eller Benz-plan

På grund av cirkelns väsentliga roll (betraktad som den icke-degenererade koniska i ett projektivt plan ) och planbeskrivningen av de ursprungliga modellerna är de tre typerna av geometrier subsumerade till plana cirkelgeometrier eller för att hedra Walter Benz, som ansåg dessa geometriska strukturer från en gemensam synvinkel, Benz-plan.

Se även

Francis Buekenhout (1981) "Les plans de Benz", Journal of Geometry 17(1):61–8.

externa länkar

Benz plan från Encyclopedia of Mathematics
Erich Hartmann Planar Circle Geometries, en introduktion till Moebius-, Laguerre- och Minkowski-plan från Darmstadts tekniska universitet