Hexapentakis trunkerad icosahedron
| Hexapentakis trunkerad icosahedron | |
|---|---|

|
|
| Conway notation | ktI |
| Geodetisk polyeder | {3,5+} 3,0 |
| Ansikten | 180 |
| Kanter | 270 |
| Vertices | 92 |
| Ansiktskonfiguration |
(60) V5.6.6 (120) V6.6.6 |
| Symmetrigrupp | Icosahedral ( I h ) |
| Dubbel polyeder | Stympad pentakis dodekaeder |
| Egenskaper | konvex |
Den hexapentakis trunkerade icosahedron är en konvex polyeder konstruerad som en förstärkt trunkerad icosahedron . Det är en geodetisk polyeder {3,5+} 3,0 , med femvärda hörn åtskilda av ett kantrikt avstånd på 3 steg.
Konstruktion
Geodetiska polyedrar är konstruerade genom att dela upp ytor av enklare polyedrar och sedan projicera de nya hörnen på ytan av en sfär. En geodetisk polyeder har raka kanter och plana ytor som närmar sig en sfär, men den kan också göras som en sfärisk polyeder (En tessellation på en sfär ) med äkta geodetiska böjda kanter på ytan av en sfär. och sfäriska triangelytor .
| Conway | u 3 I = (kt)I | (k5)k6tI | (k)tI | Sfärisk ktI |
|---|---|---|---|---|
| Bild |  |
 |
 |
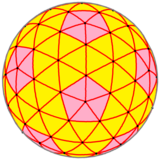
|
| Form |
3-frekvens uppdelad icosahedron |
1-frekvens underdelad hexakis trunkerad icosahedron |
1-frekvens uppdelad trunkerad icosahedron |
Sfärisk polyeder |
Besläktade polyedrar
| Polyeder | Stympad Icosahedron | #Pentakis stympad Icosahedron | #Hexakis stympad Icosahedron | Hexapentakis stympad Icosahedron |
|---|---|---|---|---|
| Bild |

|

|

|

|
| Conway | tI | k5tI | k6tI | k5k6tI |
Pentakis stympad icosahedron
| Pentakis stympad icosahedron | |
|---|---|

|
|
| Conway notation | k5tI |
| Ansikten |
132: 60 trianglar 20 hexagoner |
| Kanter | 90 |
| Vertices | 72 |
| Symmetrigrupp | Icosahedral ( I h ) |
| Dubbel polyeder | Pentatruncated pentakis dodecahedron |
| Egenskaper | konvex |
Pentakis trunkerade icosahedron är en konvex polyeder konstruerad som en förstärkt trunkerad icosahedron , som lägger till pyramider till de 12 femkantiga ytorna, vilket skapar 60 nya triangulära ytor.
Det är geometriskt likt ikosaedern där de 20 triangulära ytorna är uppdelade med en central hexagon och 3 hörntrianglar.
Dubbel
Dess dubbla polyeder kan kallas en femkantig pentakis dodekaeder , en dodekaeder , med sina hörn förstärkta av femkantiga pyramider, och sedan trunkerade spetsen av dessa pyramider, eller lägga till ett femkantigt prisma till varje vända mot dodekaedern. Det är nätet av ett dodekaedriskt prisma .
Hexakis stympad icosahedron
| Hexakis stympad icosahedron | |
|---|---|

|
|
| Conway notation | k6tI |
| Ansikten |
132: 120 trianglar 12 femhörningar |
| Kanter | 210 |
| Vertices | 80 |
| Symmetrigrupp | Icosahedral ( I h ) |
| Dubbel polyeder | Hexatrunkerad pentakis dodekaeder |
| Egenskaper | konvex |
Den hexakis trunkerade icosahedronen är en konvex polyeder konstruerad som en förstärkt trunkerad icosahedron , som lägger till pyramider till de 20 sexkantiga ytorna, vilket skapar 120 nya triangulära ytor.
Den liknar visuellt den kirala snubdodekaedern som har 80 trianglar och 12 femhörningar.
Dubbel
Den dubbla polyhedronen kan ses som en hexatruncated pentakis dodecahedron , en dodecahedron med dess ytor förstärkta av pentagonala pyramider (en pentakis dodecahedron ), och sedan dess 6-valans hörn trunkerade.
Den har liknande grupper av oregelbundna femhörningar som den femkantiga hexekontaedern .
Se även
- Antony Pugh, Polyhedra: a visual approach , 1976, kapitel 6. The Geodesic Polyhedra of R. Buckminster Fuller and Related Polyhedra
- Wenninger, Magnus (1979), Spherical Models , Cambridge University Press , ISBN 978-0-521-29432-4 , MR 0552023 , arkiverad från originalet den 4 juli 2008 Återtryckt av Dover 1999 ISBN 978-40-916- 4
externa länkar
- VTML polyhedral generator Prova "ktI" ( Conway polyhedron notation )

