Dodekaedriskt prisma
| Dodekaedriskt prisma | |
|---|---|
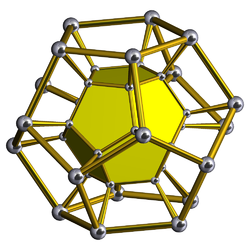 Schlegeldiagram Endast en dodekaedrisk cell visas |
|
| Typ | Prismatisk enhetlig 4-polytop |
| Enhetligt index | 57 |
| Schläfli symbol | t{2,3,5} eller {5,3}×{} |
| Coxeter-Dynkin |
|
| Celler |
2 ( 5.5.5 ) 12 ( 4.4.5 ) |
| Ansikten |
30 {4} 24 {5} |
| Kanter | 80 |
| Vertices | 40 |
| Vertex figur |
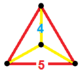 Liksidig-triangulär pyramid |
| Dubbel | Ikosaedrisk bipyramid |
| Symmetrigrupp | [5,3,2], order 240 |
| Egenskaper | konvex |
I geometri är ett dodekaedriskt prisma en konvex enhetlig 4-polytop . Denna 4-polytop har 14 polyedriska celler: 2 dodekaedrar förbundna med 12 pentagonala prismor . Den har 54 ansikten: 30 rutor och 24 femhörningar. Den har 80 kanter och 40 hörn.
Den kan konstrueras genom att skapa två sammanfallande dodekaedrar i 3-utrymme, och översätta varje kopia i motsatta vinkelräta riktningar i 4-utrymme tills deras separation är lika med deras kantlängd.
Det är en av 18 konvexa likformiga polyedriska prismor som skapats genom att använda enhetliga prismor för att koppla ihop par av parallella platoniska fasta eller arkimediska fasta ämnen .
Alternativa namn
- Dodekaedriskt dyadiskt prisma Norman W. Johnson
- Dodekaedriskt hyperprisma
Bilder
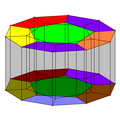
Transparent Schlegel-diagram
En ortografisk projektion med en trådramsmodell och har hälften av de femkantiga ytorna färgade för att visa de två dodekaedrarna. Dodekaedrarna är regelbundna, men ser tillplattade ut på grund av projektionen och visningsriktningen.
Strukturera
Det dodekaedriska prismat består av två dodekaedrar kopplade till varandra via 12 femkantiga prismor. De femkantiga prismorna är förenade med varandra via sina fyrkantiga ytor.
Projektioner
Den femkantiga prisma-första ortografiska projektionen av det dodekaedriska prismat i 3D-rymden har ett dekagonalt hölje (se diagram). Två av de femkantiga prismorna skjuter ut mot mitten av denna volym, var och en omgiven av 5 andra femkantiga prismor. De bildar två uppsättningar (vardera bestående av ett centralt femkantigt prisma omgivet av 5 andra olikformiga femkantiga prismor) som täcker volymen av det dekagonala prismat två gånger. De två dodekaedrarna projicerar på kuvertets dekagonala ytor.
Den dodekaedriska första ortografiska projektionen av det dodekaedriska prismat i 3D-rymden har ett dodekaedriskt hölje. De två dodekaedriska cellerna projicerar på hela volymen av detta hölje, medan de 12 dekagonala prismiska cellerna projicerar på dess 12 femkantiga ytor.
externa länkar
- 6. Konvex uniform prismatisk polychora - Modell 57 , George Olshevsky.
- Klitzing, Richard. "4D enhetliga polytoper (polychora) x o3o5x - dope" .