Grundläggande teorem om homomorfismer
I abstrakt algebra relaterar den fundamentala satsen om homomorphisms , även känd som den fundamentala homomorphism theorem , eller den första isomorphism theorem , strukturen av två objekt mellan vilka en homomorphism ges, och av kärnan och bilden av homomorphism.
Homomorfismsatsen används för att bevisa isomorfismsatserna .
Gruppteoretisk version
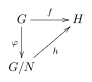
Givet två grupper G och H och en grupp homomorfism f : G → H , låt N vara en normal undergrupp i G och φ den naturliga surjektiva homomorfismen G → G / N (där G / N är kvotgruppen av G med N ). Om N är en delmängd av ker ( f ) så finns det en unik homomorfism h : G / N → H så att f = h ∘φ .
Med andra ord är den naturliga projektionen φ universell bland homomorfismer på G som mappar N till identitetselementet .
Situationen beskrivs av följande kommutativa diagram :
h är injektiv om och endast om N = ker( f ) . Därför, genom att sätta N = ker( f ) får vi omedelbart den första isomorfismsatsen .
Vi kan skriva påståendet i grundsatsen om homomorfismer av grupper som "varje homomorf bild av en grupp är isomorf till en kvotgrupp".
Andra versioner
Liknande satser är giltiga för monoider , vektorrum , moduler och ringar .
Se även
- Beachy, John A. (1999), "Theorem 1.2.7 (The fundamental homomorphism theorem)", Introduktionsföreläsningar om ringar och moduler , London Mathematical Society Student Texts, vol. 47, Cambridge University Press, sid. 27, ISBN 9780521644075 .
- Grove, Larry C. (2012), "Theorem 1.11 (The Fundamental Homomorphism Theorem)", Algebra , Dover Books on Mathematics, Courier Corporation, sid. 11, ISBN 9780486142135 .
- Jacobson, Nathan (2012), "Fundamental theorem on homomorphisms of Ω-algebras", Basic Algebra II , Dover Books on Mathematics (2nd ed.), Courier Corporation, sid. 62, ISBN 9780486135212 .
- Rose, John S. (1994), "3.24 Fundamental theorem on homomorphisms", A course on Group Theory [reprint of the 1978 original] , Dover Publications, Inc., New York, s. 44–45, ISBN 0-486- 68194-7 , MR 1298629 .