Genomskärning

Skärningspunkten (röd) mellan två skivor (vit och röd med svarta gränser).

Cirkeln (svart) skär linjen (lila) i två punkter (röd) . Skivan (gul) skär linjen i linjesegmentet mellan de två röda punkterna.

Skärningen mellan D och E visas i grålila. Skärningen av A med någon av B, C, D eller E är den tomma mängden .

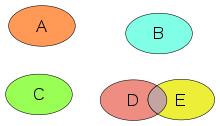
I matematik är skärningspunkten mellan två eller flera objekt ett annat objekt som består av allt som finns i alla objekt samtidigt. Till exempel, i euklidisk geometri , när två linjer i ett plan inte är parallella, är deras skärningspunkt den punkt där de möts. Mer allmänt, i mängdteorin , definieras skärningspunkten av mängder som den uppsättning element som tillhör dem alla. Till skillnad från den euklidiska definitionen, förutsätter detta inte att föremålen i fråga ligger i ett gemensamt utrymme .

Skärning är ett av de grundläggande begreppen inom geometri . En skärning kan ha olika geometriska former , men en punkt är den vanligaste i en plan geometri . Incidensgeometri definierar en skärningspunkt (vanligtvis av lägenheter ) som ett objekt med lägre dimensioner som faller samman med vart och ett av de ursprungliga objekten. I detta tillvägagångssätt kan en skärning ibland vara odefinierad, till exempel för parallella linjer . I båda fallen bygger begreppet skärningspunkt på logisk konjunktion . Algebraisk geometri definierar korsningar på sitt eget sätt med korsningsteori .

Unikhet

Det kan finnas mer än ett primitivt objekt, till exempel punkter (bilden ovan), som bildar en skärningspunkt. Korsningen kan ses kollektivt som alla delade objekt (dvs. korsningsoperationen resulterar i en uppsättning , möjligen tom), eller som flera skärningsobjekt ( möjligen noll ).

I mängdlära

Om man anser att en väg motsvarar uppsättningen av alla dess platser, motsvarar en vägkorsning (cyan) mellan två vägar (grön, blå) korsningen mellan deras uppsättningar.

Skärningen av två uppsättningar A och B är uppsättningen av element som finns i både A och B. Formellt,

A\cap B=\{x:x\in A{\text{ och }}x\in B\}

.

Till exempel, om $A=\{1,3,5,7\}$ och $B=\ {1,2,4,6\}$ , sedan $A\cap B=\{1\}$ . Ett mer utarbetat exempel (som involverar oändliga mängder) är:

A = { x är ett jämnt heltal }

B = { x är ett heltal delbart med 3}

A\cap B=\{6,12,18,\ prickar \}

inte talet 5 i skärningspunkten mellan uppsättningen primtal {2, 3, 5, 7, 11, …} och uppsättningen av jämna tal {2, 4, 6, 8, 10, … }, för även om 5 är ett primtal är det inte jämnt. Faktum är att siffran 2 är den enda siffran i skärningspunkten mellan dessa två uppsättningar. I det här fallet har skärningspunkten matematisk betydelse: talet 2 är det enda jämna primtalet.

I geometri

Den röda pricken representerar punkten där de två linjerna skär varandra.

Inom geometri är en skärningspunkt en punkt, linje eller kurva som är gemensam för två eller flera objekt (som linjer, kurvor, plan och ytor). Det enklaste fallet i euklidisk geometri är linje-linje skärningen mellan två distinkta linjer , som antingen är en punkt eller inte existerar (om linjerna är parallella ). Andra typer av geometriska skärningspunkter inkluderar:

Bestämning av skärningspunkten mellan plattor – linjära geometriska objekt inbäddade i ett högre dimensionellt utrymme – är en enkel uppgift för linjär algebra , nämligen lösningen av ett system av linjära ekvationer . I allmänhet leder bestämningen av en skärningspunkt till icke-linjära ekvationer, som kan lösas numeriskt , till exempel med Newton-iteration . Skärningsproblem mellan en linje och en konisk sektion (cirkel, ellips, parabel, etc.) eller en kvadrik (sfär, cylinder, hyperboloid, etc.) leder till andragradsekvationer som lätt kan lösas. Skärningar mellan kvadriker leder till kvartekvationer som kan lösas algebraiskt .

Notation

Skärningspunkten betecknas med U+2229 ∩ INTERSECTION från Unicode Mathematical Operators .

Symbolen U+2229 ∩ användes först av Hermann Grassmann i Die Ausdehnungslehre von 1844 som allmän operationssymbol, inte specialiserad för korsning. Därifrån användes den av Giuseppe Peano (1858–1932) för korsning, 1888 i Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann .

Peano skapade också de stora symbolerna för allmän korsning och förening av mer än två klasser i sin bok Formulario mathematico från 1908 .

Se även

Konstruktiv solid geometri , Boolean Intersection är ett av sätten att kombinera 2D/3D-former
Dimensionellt utökad 9-korsningsmodell
Möt (gitterteori)
Skärning (mängdlära)
Union (mängdlära)

^ Vereshchagin, Nikolai Konstantinovich; Shen, Alexander (2002-01-01). Grundläggande mängdteori . American Mathematical Soc. ISBN 9780821827314 .
^ Peano, Giuseppe (1888-01-01). Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann: preceduto dalle operazioni della logica deduttiva (på italienska). Torino: Fratelli Bocca.
^ Cajori, Florian (2007-01-01). En historia av matematiska notationer . Torino: Cosimo, Inc. ISBN 9781602067141 .
^ Peano, Giuseppe (1908-01-01). Formulario mathematico, tomo V (på italienska). Torino: Edizione cremonese (Faksimile-Reprint i Rom, 1960). sid. 82. OCLC 23485397 .
^ Tidigast användningar av symboler av uppsättningsteori och logik

externa länkar

Weisstein, Eric W. "Skärning" . MathWorld .

[:0-1] Vereshchagin, Nikolai Konstantinovich; Shen, Alexander (2002-01-01). Grundläggande mängdteori . American Mathematical Soc. ISBN 9780821827314 .

[:1-2] Peano, Giuseppe (1888-01-01). Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann: preceduto dalle operazioni della logica deduttiva (på italienska). Torino: Fratelli Bocca.

[:2-3] Cajori, Florian (2007-01-01). En historia av matematiska notationer . Torino: Cosimo, Inc. ISBN 9781602067141 .

[:3-4] Peano, Giuseppe (1908-01-01). Formulario mathematico, tomo V (på italienska). Torino: Edizione cremonese (Faksimile-Reprint i Rom, 1960). sid. 82. OCLC 23485397 .

[5] Tidigast användningar av symboler av uppsättningsteori och logik