Entanglement destillation

Entanglement-destillation (även kallad entanglement-rening ) är omvandlingen av N kopior av ett godtyckligt intrasslat tillstånd $\rho$ till ett visst antal ungefärligen rena Bell-par , med endast lokala funktioner och klassisk kommunikation .

Kvantintrasslingsdestillation kan på detta sätt övervinna den degenerativa påverkan av bullriga kvantkanaler genom att omvandla tidigare delade mindre intrasslade par till ett mindre antal maximalt intrasslade par.

Historia

Gränserna för intrasslingsspädning och destillation beror på CH Bennett , H. Bernstein, S. Popescu och B. Schumacher , som presenterade de första destillationsprotokollen för rena tillstånd 1996; Destillationsprotokoll för entanglement för blandade tillstånd infördes av Bennett, Brassard , Popescu, Schumacher, Smolin och Wootters samma år. Bennett, DiVincenzo , Smolin och Wootters etablerade kopplingen till kvantfelskorrigering i ett banbrytande dokument som publicerades i augusti 1996, också i tidskriften Physical Review, vilket har stimulerat en hel del efterföljande forskning.

Kvantifierande förveckling

Ett två qubit- system kan skrivas som en överlagring av möjliga beräkningsbaserade qubit-tillstånd: ${\displaystyle |00\rangle ,|01\rangle ,|10\rangle ,|11\rangle } , var och en$ med en tillhörande komplex koefficient $\alpha \,\!$ :

|\psi \rangle =\alpha _{00}|00\rangle +\alpha _{01}|01\rangle +\alpha _{10}|10\rangle +\alpha _{11} |11\rangle

Liksom i fallet med en enskild kvantbit, tillståndet sannolikheten för att mäta en viss beräkningsbas $|x\rangle$ är kvadraten på modulen för dess amplitud, eller tillhörande koefficient, $|\alpha _{x}|^{2}\,\!$ , med förbehåll för normaliseringsvillkoret ${\textstil \summa _{x\in {0,1}}|\alpha _{x}|^{2}=1}$ . Normaliseringsvillkoret garanterar att summan av sannolikheterna summerar till 1, vilket betyder att vid mätning kommer ett av tillstånden att observeras.

Bell-tillståndet är ett särskilt viktigt exempel på ett två qubit-tillstånd: ${\textstyle {\frac {1}{\sqrt {2}}}(|00\rangle +|11 \rangle )}$

Bellstater har egenskapen att mätresultat på de två qubitarna är korrelerade. Som framgår av uttrycket ovan är de två möjliga mätutfallen noll och ett, båda med en sannolikhet på 50 %. Som ett resultat ger en mätning av den andra qubiten alltid samma resultat som mätningen av den första qubiten.

Klocktillstånd kan användas för att kvantifiera intrassling. Låt m vara antalet högfientliga kopior av en Bell-tillstånd som kan produceras med LOCC. Givet ett stort antal Bell-tillstånd är mängden intrassling närvarande i ett rent tillstånd $|\psi \rangle$ kan sedan definieras som förhållandet mellan ${\displaystyle n/m} , [$ förtydligande ^{behövs ] som} kallas den destillerbara intrasslingen av ett visst tillstånd ${\displaystyle |\phi \rangle } ,$ [ ^{förtydligande behövs ]} som ger ett kvantifierat mått på mängden intrassling som finns i ett givet system. Processen med intrasslingsdestillation syftar till att mätta detta begränsande förhållande. Antalet kopior av ett rent tillstånd som kan omvandlas till ett maximalt intrasslat tillstånd är lika med von Neumann-entropin $S(p)$ för tillståndet, vilket är en förlängning av begreppet klassisk entropi för kvantsystem. Matematiskt, för en given densitetsmatris ${\displaystyle p} ,$ är von Neumann-entropin $S(p)$ $S( p)=-\mathrm {Tr} (p\ln p)$ . Entanglement kan sedan kvantifieras som entropin för entanglement, vilket är von Neumann-entropin för antingen $p_{A}$ eller $p_{B}$ som:

E=-\mathrm {Tr} (p_{A}\ln p_{A})= -\mathrm {Tr} (p_{B}\ln p_{B}),

Vilket sträcker sig från 0 för ett produkttillstånd till $\ln 2$ för ett maximalt intrasslat tillstånd (om $\ln$ ersätts med $\log _{2}$ då maximalt intrasslad har värdet 1).

Motivering

Antag att två parter, Alice och Bob , skulle vilja kommunicera klassisk information över en bullrig kvantkanal. Antingen klassisk eller kvantinformation kan sändas över en kvantkanal genom att koda informationen i ett kvanttillstånd. Med denna kunskap kodar Alice den klassiska informationen som hon avser att skicka till Bob i ett (kvant)produkttillstånd, som en tensorprodukt av matriser med reducerad densitet $p_{1}\otimes p_{ 2}\otimes \cdots$ där varje $p$ är diagonal och kan endast användas som engångsinmatning för en viss kanal $\epsilon$ .

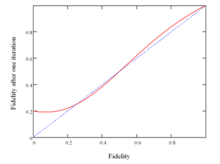
Tillförlitligheten hos den brusiga kvantkanalen är ett mått på hur mycket utsignalen från en kvantkanal liknar ingången, och är därför ett mått på hur väl en kvantkanal bevarar information. Om ett rent tillstånd $\psi$ sänds in i en kvantkanal framträder som det tillstånd som representeras av densitetsmatrisen $p$ , definieras sändningstroheten som $F=\langle \psi |p|\psi \rangle$ .

Problemet som Alice och Bob nu står inför är att kvantkommunikation över stora avstånd beror på framgångsrik distribution av mycket intrasslade kvanttillstånd , och på grund av oundvikligt brus i kvantkommunikationskanaler, minskar kvaliteten på intrasslade tillstånd i allmänhet exponentiellt med kanallängden som en funktion av kanalens trohet. Entanglement-destillation tar itu med detta problem med att upprätthålla en hög grad av intrassling mellan distribuerade kvanttillstånd genom att omvandla N kopior av ett godtyckligt intrasslat tillstånd $\rho$ till ungefär $S(\rho )N$ Bell par, med endast lokala operationer och klassisk kommunikation. Målet är att dela starkt korrelerade qubits mellan avlägsna parter (Alice och Bob) för att möjliggöra tillförlitlig kvantteleportation eller kvantkryptografi .

Intrasslingskoncentration

Rena stater

Den nya troheten efter en iteration av destillationsprotokollet för rena tillstånd.

Med tanke på n partiklar i singletttillståndet som delas mellan Alice och Bob, kommer lokala handlingar och klassisk kommunikation att räcka för att förbereda godtyckligt bra kopior av $\phi$ med en avkastning

{\displaystyle {\frac {m}{n}}\to {\frac {1}{E(\phi )}}} som

n

\displaystyle n\to \infty }

.

Låt ett intrasslat tillstånd $|\psi \rangle$ har en Schmidt-nedbrytning :

|\psi \rangle =\summa _{x}{\sqrt {p(x)}}|x_{A}\rangle |x_{B}\rangle

där koefficienterna p(x) bildar en sannolikhetsfördelning , och därmed värderas positivt och summeras till enhet . Tensorprodukten för detta tillstånd är då,

|\psi \rangle ^{\otimes m}=\summa _{x_{1},x_{2},\dots ,x_{m}}{\ sqrt {p(x_{1})p(x_{2})\dots p(x_{m})}}|x_{1A}x_{2A}\dots x_{mA}\rangle |x_{1B}x_ {2B}\dots x_{mB}\rangle

Nu, utelämna alla termer $x_{1},\dots ,x_{m}$ som inte ingår i någon sekvens som sannolikt kommer att inträffa med hög sannolikhet, känd som den typiska mängden : $A_{\epsilon }^{(n)}$ det nya tillståndet är

|\phi _{m}\rangle =\summa _{x\epsilon A_{\epsilon }^{(n)}}{\sqrt {p(x_ {1})p(x_{2})\dots p(x_{m})}}|x_{1A}x_{2A}\dots x_{mA}\rangle |x_{1B}x_{2B}\dots x_{mB}\rangle

Och åternormalisera,

|\phi _{m}'\rangle ={\frac {|\phi _{m}\rangle }{\sqrt {\langle \phi _{m}|\phi _{m} \rangle }}}

Sedan troheten

F(|\psi \rangle ^{\otimes m},|\phi _{m}^{'}\rangle )\to 1

som

m\to \infty

.

Antag att Alice och Bob är i besittning av m kopior av $|\psi \rangle$ . Alice kan utföra en mätning på den typiska mängden $A_{\epsilon }^{(n)}$ delmängd av $p_{\psi }\,\!$ , vilket konverterar tillståndet $|\psi \rangle ^{\otimes m}\rightarrow |\phi _{m}\rangle$ med hög trohet. Satsen för typiska sekvenser visar oss sedan att $1-\delta$ är sannolikheten att den givna sekvensen är en del av den typiska mängden, och kan göras godtyckligt nära 1 för tillräckligt stor m, och därför Schmidt-koefficienter för det renormaliserade Bell-tillståndet $|\phi _{m}'\rangle$ ${\textstyle {1}/{\sqrt {1-\delta }}}$ högst en faktor . Alice och Bob kan nu få en mindre uppsättning av n Bell-tillstånd genom att utföra LOCC på staten $|\phi _{m}'\rangle$ med vilken de kan övervinna bruset från en kvantkanal för att kommunicera framgångsrikt.

Blandade stater

Den nya troheten efter en iteration av destillationsprotokollet som presenteras här för blandade tillstånd

Många tekniker har utvecklats för att utföra intrasslingsdestillation för blandade tillstånd, vilket ger en lägre gräns för värdet av den destillerbara intrasslingen $D(p)$ för specifika klasser av tillstånd $p$ .

En vanlig metod innebär att Alice inte använder den brusiga kanalen för att sända källtillstånd direkt utan istället förbereder ett stort antal Bell-tillstånd, och skickar hälften av varje Bell-par till Bob. Resultatet från överföring genom den brusiga kanalen är att skapa det blandade intrasslade tillståndet $p$ , så att Alice och Bob slutar med att dela $m$ kopior av $p$ . Alice och Bob utför sedan entanglement-destillation och producerar $m\cdot D(p)$ nästan perfekt intrasslade tillstånd från de blandade entangled-tillstånden $p$ genom att utföra lokala enhetsoperationer och mätningar på delade intrasslade par, koordinerade sina handlingar genom klassiska budskap och offrade några av de intrasslade paren för att öka renheten hos de återstående. Alice kan nu förbereda ett $m\cdot D(p)$ qubit-tillstånd och teleportera det till Bob med hjälp av $m\cdot D(p)$ Bell-par som de delar med hög trohet. Vad Alice och Bob sedan effektivt har åstadkommit är att ha simulerat en ljudlös kvantkanal med hjälp av en bullrig, med hjälp av lokala handlingar och klassisk kommunikation.

Låt $M$ vara ett allmänt blandat tillstånd av två spin-1/2- partiklar som kunde ha resulterat från överföringen av ett initialt rent singletttillstånd

\psi ^{-}=(\uparrow \downarrow -\downarrow \uparrow )/{\sqrt {2}}

genom en bullrig kanal mellan Alice och Bob, som kommer att användas för att destillera någon ren förveckling. Troheten hos

M

F=\langle \psi ^{-}|M|\psi ^{-}\rangle

är ett bekvämt uttryck för sin renhet i förhållande till en perfekt singlet. Antag att M redan är ett rent tillstånd av två partiklar

M=|\phi \rangle \langle \phi |

för vissa

\phi

. Entanglementet för

{\displaystyle \phi } ,

som redan fastställts, är von Neumann-entropin

E(\phi )=S(p_{A })=S(p_{B})

där

p_{A}=\operatörsnamn {tr} _{B}^{}(|\phi \rangle \langle \phi |),

och likaså representerar

p_{B}

matriserna med reducerad densitet för endera partikeln. Följande protokoll används då:

Genom att utföra en slumpmässig bilateral rotation på varje delat par, välja en slumpmässig SU(2) -rotation oberoende för varje par och applicera den lokalt på båda medlemmarna av paret omvandlar det initiala allmänna tvåspinnsblandade tillståndet M till en rotationssymmetrisk blandning av singletten tillstånd $\psi ^{-}$ och de tre tripletttillstånden $\psi ^{+}$ och $\phi ^{\pm }$ : $W_{F}=F\cdot |\psi ^{-}\rangle \langle \psi ^{-}|+{\frac {1-F}{3}}|\phi ^{+}\ rangle \langle \phi ^{+}|+{\frac {1-F}{3}}|\psi ^{+}\rangle \langle \psi ^{+}|+{\frac {1-F} {3}}|\phi ^{-}\rangle \langle \phi ^{-}|$ Werner- tillståndet $W_{F}$ har samma renhet F som det initiala blandade tillståndet M från vilket det härleddes på grund av singlettens invarians under bilaterala rotationer.
Vart och ett av de två paren påverkas sedan av en ensidig rotation, som vi kan kalla ${\displaystyle \sigma _{y}} ,$ vilket har effekten att omvandla dem från huvudsakligen $\psi ^{- }$ Werner anger till huvudsakligen $\phi ^{+}$ tillstånd med en stor komponent $F>{\frac {1}{2}}$ av $\ phi ^{+}$ medan komponenterna i de andra tre Bell-tillstånden är lika.
De två orena $\phi ^{+}$ tillstånden påverkas sedan av en bilateral XOR , och efteråt mäts målparet lokalt längs z-axeln. Det omätade källparet behålls om målparets snurr kommer ut parallella som i fallet med båda ingångarna är sanna $\phi ^{+}$ tillstånd; och det kasseras annars.
Om källparet inte har förkastats konverteras det tillbaka till ett övervägande $\psi ^{-}$ tillstånd genom en ensidig $\sigma _{y}$ rotation och görs rotationssymmetrisk av en slumpmässig bilateral rotation.

Genom att upprepa det skisserade protokollet ovan destilleras Werner-tillstånd vars renhet kan väljas att vara godtyckligt hög $F_{\text{out}}<1$ från en samling M av inmatade blandade renhetstillstånd ${\textstyle F_{\text{in}}>{\frac {1}{2}}}$ men med en avkastning som tenderar mot noll i gränsen $F_{\text{out}}\ till 1$ . Genom att utföra ytterligare en bilateral XOR-operation, den här gången på ett variabeltal ${\textstil k(F)\approx {\frac {1}{\sqrt {1-F}}}}$ av källan par, i motsats till 1, i varje målpar innan det mäts, kan avkastningen fås att närma sig en positiv gräns som $F_{\text{out}}\to 1$ . Denna metod kan sedan kombineras med andra för att få en ännu högre avkastning.

Procrustean metod

Procrustean-metoden för intrasslingskoncentration kan användas för så lite som ett delvis intrasslat par, och är effektivare än Schmidt-projektionsmetoden för intrassling av mindre än 5 par, och kräver att Alice och Bob känner till biasen ( θ {\displaystyle \ $}$ ) av de n paren i förväg. Metoden har fått sitt namn från Procrustes eftersom den producerar ett perfekt intrasslat tillstånd genom att skära bort den extra sannolikheten som är förknippad med den större termen i den partiella intrasslingen av de rena tillstånden:

\cos \theta \left|\uparrow _{A}\right\rangle \otimes \left|\downarrow _{B}\right\rangle -\sin \theta \left|\downarrow _{ A}\right\rangle \otimes \left|\uparrow _{B}\right\rangle

Om man antar en samling partiklar för vilka $\theta$ är känd som antingen mindre än eller större än $\pi /4$ kan Procrustean-metoden utföras genom att behålla alla partiklar som, när de passerar genom en polarisationsberoende absorbator, eller en polarisationsberoende reflektor, som absorberar eller reflekterar en bråkdel $\tan ^{2}\theta$ av det mer sannolika resultatet, absorberas eller avböjs inte. Därför, om Alice har partiklar för vilka ${\displaystyle \theta \neq \pi /4} ,$ kan hon separera ut partiklar som är mer sannolikt att mätas i upp/ned-basen och lämnas med partiklar i maximalt blandat tillstånd av snurr upp och ner. Denna behandling motsvarar en POVM (positive-operator-valued measurement). För att få ett perfekt intrasslat tillstånd av två partiklar, informerar Alice Bob om resultatet av hennes generaliserade mätning medan Bob inte mäter sin partikel alls utan istället kastar bort sin om Alice kastar sin.

Stabilisatorprotokoll

Syftet med ett $\left[n,k\right]$ entanglement destillationsprotokoll är att destillera $k$ rena ebitar från $n$ brusiga ebitar där $0\leq k\leq n$ . Utbytet av ett sådant protokoll är $k/n$ . Två parter kan sedan använda de brusfria ebitarna för kvantkommunikationsprotokoll .

De två parterna upprättar en uppsättning delade bullriga ebitar på följande sätt. Avsändaren Alice förbereder först $n$ Bell tillstånd $\left\vert \Phi ^{+}\right\rangle ^{\otimes n}$ lokalt. Hon skickar den andra qubiten av varje par över en brusig kvantkanal till en mottagare Bob. Låt $\left\vert \Phi _{n}^{+}\right\rangle$ vara tillståndet $\left\vert \Phi ^{+}\right\rangle ^{\otimes n}$ omarrangerade så att alla Alices qubits är till vänster och alla Bobs qubits är till höger. Den brusiga kvantkanalen tillämpar ett Pauli-fel i feluppsättningen ${\mathcal {E}}\subset \Pi ^{n}$ på uppsättningen av $n$ qubits som skickas över kanalen . Avsändaren och mottagaren delar sedan en uppsättning av $n$ brusiga ebitar av formuläret ${\displaystyle \left(\mathbf {I} \otimes \mathbf {A} \right)\left\vert \Phi _{n}^{+}\right\rangle } där identiteten$ I $\ displaystyle \mathbf {I} }$ agerar på Alices qubits och $\mathbf {A}$ är någon Pauli-operator i ${\mathcal {E}}$ som agerar på Bobs qubits .

Ett envägsstabilisatorintrasslingsdestillationsprotokoll använder en stabilisatorkod för destillationsproceduren. Antag att stabilisatorn ${\mathcal {S}}$ för en $\left[n,k\right]$ kvantfelskorrigerande kod har generatorer $g_{1},\ldots ,g_{nk}$ . Destillationsproceduren börjar med att Alice mäter n $nk$ -generatorerna i ${\mathcal {S}$ . Låt $\left\{\mathbf {P} _{i}\right\}$ vara uppsättningen av de $2^{nk}$ projektorerna som projicerar på $2^{nk}$ ortogonala delrum som motsvarar generatorerna i ${\mathcal {S}}$ . Mätningsprojekten $\left\vert \Phi _{n}^{+}\right\rangle$ _ _ slumpmässigt på ett av i $\displaystyle i}$ underrymden. Varje $\mathbf {P} _{i}$ pendlar med den bullriga operatorn $\mathbf {A}$ på Bobs sida så att

\left(\mathbf {P} _{i}\otimes \mathbf {I} \right)\left(\mathbf {I} \otimes \mathbf {A} \right)\left\vert \Phi _ {n}^{+}\right\rangle =\left(\mathbf {I} \otimes \mathbf {A} \right)\left(\mathbf {P} _{i}\otimes \mathbf {I} \ höger)\left\vert \Phi _{n}^{+}\right\rangle .

Följande viktiga klocktillståndsmatrisidentitet gäller för en godtycklig matris $\mathbf {M}$ :

\left(\mathbf {M} \otimes \mathbf {I} \right)\left\vert \Phi _{n}^{+}\right\rangle =\left(\mathbf {I} \otimes \mathbf {M} ^{T}\right)\left\vert \Phi _{n}^{+}\right\rangle .

Då är uttrycket ovan lika med följande:

\left(\mathbf {I} \otimes \mathbf {A} \right)\left(\mathbf {P} _{i}\otimes \mathbf {I} \right)\left\vert \Phi _ {n}^{+}\right\rangle =\left(\mathbf {I} \otimes \mathbf {A} \right)\left(\mathbf {P} _{i}^{2}\otimes \mathbf {I} \right)\left\vert \Phi _{n}^{+}\right\rangle =\left(\mathbf {I} \otimes \mathbf {A} \right)\left(\mathbf {P } _{i}\otimes \mathbf {P} _{i}^{T}\right)\left\vert \Phi _{n}^{+}\right\rangle .

Därför projicerar var och en av Alices projektorer

\mathbf {P} _{i}

Bobs qubits på ett delrum

\mathbf {P} _{i}^{T}

som motsvarar Alices projicerat delrum

\mathbf {P} _{i}

. Alice återställer sina qubits till det samtidiga +1- egenutrymmet för generatorerna i

{\mathcal {S}}

. Hon skickar sina mätresultat till Bob. Bob mäter generatorerna i

{\mathcal {S}}

. Bob kombinerar sina mätningar med Alices för att fastställa ett syndrom för felet. Han utför en återställningsoperation på sina qubits för att vända felet. Han återställer sina qubits

{\mathcal {S}}

. Alice och Bob utför båda den enhetliga avkodningen som motsvarar stabilisatorn

{\mathcal {S}}

för att konvertera sina

k

logiska ebitar till

k

fysiska ebitar .

Entanglement-assisterad stabilisatorkod

Luo och Devetak gav en enkel förlängning av ovanstående protokoll (Luo och Devetak 2007). Deras metod omvandlar en entanglement-assisterad stabilisatorkod till ett entanglement-assisterad entanglement-destillationsprotokoll.

Luo och Devetak bildar ett entanglement destillation protokoll som har entanglement assistans från några ljudlösa ebits . Det avgörande antagandet för ett entanglement-assisterat entanglement-destillationsprotokoll är att Alice och Bob har $c$ ljudlösa ebitar utöver sina $n$ brusiga ebits . Det totala tillståndet för de bullriga och ljudlösa ebitarna är

\left(\mathbf {I} ^{A}\otimes \left(\mathbf {A\otimes I} \right)^{B}\right)\left\vert \Phi _{n+c}^{+}\right\rangle

där

\mathbf {I} ^{A}

är den

2^{n+c}\times 2^{n+c}

identitetsmatrisen som verkar på Alices qubits och den brusiga Pauli-operatorn

{\displaystyle \left(\mathbf {A\otimes I} \right)^{B}} påverkar

endast Bobs första

n

qubits . Således är de sista

c

ebitarna brusfria, och Alice och Bob måste korrigera för fel endast på de första

n

ebitarna .

Protokollet fortsätter exakt som beskrivits i föregående avsnitt. Den enda skillnaden är att Alice och Bob mäter generatorerna i en entanglement-assisterad stabilisatorkod . Varje generator spänner över $n+c$ qubits där de sista $c$ qubitarna är brusfria.

Vi kommenterar utbytet av detta förtrasslingsassisterade destillationsprotokoll. En entanglement-assisterad kod har $nk$ -generatorer som var och en har $n+c$ Pauli-poster. Dessa parametrar innebär att entanglement-destillationsprotokollet producerar $k+c$ ebitar. Men protokollet förbrukar $c$ initiala ljudlösa ebits som en katalysator för destillation. Därför är utbytet av detta protokoll $k/n$ .

Entanglement spädning

Den omvända processen för entanglement-destillation är entanglement-utspädning, där stora kopior av Bell-tillståndet omvandlas till mindre intrasslade tillstånd med hjälp av LOCC med hög kvalitet. Syftet med utspädningsprocessen för intrassling är alltså att mätta det omvända förhållandet n till m, definierat som den destillerbara trasslingen.

Ansökningar

Förutom dess viktiga tillämpning i kvantkommunikation, spelar intrasslingsrening också en avgörande roll vid felkorrigering för kvantberäkning , eftersom det avsevärt kan öka kvaliteten på logiska operationer mellan olika kvantbitar. Rollen av intrasslingsdestillation diskuteras kort för följande tillämpningar.

Kvantfelskorrigering

Entanglement-destillationsprotokoll för blandade tillstånd kan användas som en typ av felkorrigering för kvantkommunikationskanaler mellan två parter Alice och Bob, vilket gör det möjligt för Alice att på ett tillförlitligt sätt skicka mD(p) qubits av information till Bob, där D(p) är den destillerbara entanglement av p, tillståndet som uppstår när halvan av ett Bell-par skickas genom den brusiga kanalen $\epsilon$ som förbinder Alice och Bob.

I vissa fall kan intrasslingsdestillation fungera när konventionella kvantfelskorrigeringstekniker misslyckas. Entanglement destillation protokoll är kända som kan producera en överföringshastighet som inte är noll D(p) för kanaler som inte tillåter överföring av kvantinformation på grund av egenskapen att intrasslingsdestillationsprotokoll tillåter klassisk kommunikation mellan parterna i motsats till konventionell felkorrigering som förbjuder det.

Kvantkryptografi

Konceptet med korrelerade mätresultat och entanglement är centralt för kvantnyckelutbyte, och därför är förmågan att framgångsrikt utföra intrasslingsdestillation för att erhålla maximalt intrasslade tillstånd väsentlig för kvantkryptografi.

Om ett intrasslat par av partiklar delas mellan två parter, kommer alla som fångar endera partikeln att förändra det övergripande systemet, vilket gör att deras närvaro (och mängden information de har fått) kan bestämmas så länge som partiklarna är i ett maximalt intrasslat tillstånd. För att dela en hemlig nyckelsträng måste Alice och Bob också utföra teknikerna för integritetsförstärkning och informationsavstämning för att destillera en delad hemlig nyckelsträng. Informationsavstämning är felkorrigering över en offentlig kanal som stämmer av fel mellan de korrelerade slumpmässiga klassiska bitsträngarna som delas av Alice och Bob samtidigt som den begränsar kunskapen som en eventuell avlyssnare Eve kan ha om de delade nycklarna. Efter att informationsavstämning har använts för att stämma av möjliga fel mellan de delade nycklar som Alice och Bob besitter och begränsa den möjliga information som Eve kunde ha fått, används tekniken för integritetsförstärkning för att destillera en mindre delmängd av bitar som maximerar Eves osäkerhet om nyckeln.

Kvantteleportering

Vid kvantteleportering vill en avsändare sända ett godtyckligt kvanttillstånd för en partikel till en möjligen avlägsen mottagare. Kvantteleportering kan uppnå trogen överföring av kvantinformation genom att ersätta klassisk kommunikation och tidigare intrassling med en direkt kvantkanal. Med hjälp av teleportering kan en godtycklig okänd qubit troget sändas via ett par maximalt intrasslade qubits som delas mellan sändare och mottagare, och ett 2-bitars klassiskt meddelande från sändaren till mottagaren. Kvantteleportering kräver en brusfri kvantkanal för att dela perfekt intrasslade partiklar, och därför uppfyller intrasslingsdestillation detta krav genom att tillhandahålla den brusfria kvantkanalen och maximalt intrasslade kvantbitar.

Se även

Anteckningar och referenser

Kwiat, Paul G .; Barraza-Lopez, Salvador; Stefanov, André; Gisin, Nicolas (2001), "Experimentell entanglement destillation and 'hidden' non-locality", Nature , 409 ( 6823): 1014–1017, Bibcode : 2001Natur.409.1014K , doi : 10.1038 / 4010 3ID 0170 3ID 0170 3ID 3170 3170 2001 ID 4430054
Yamamoto, Takashi; Koashi, Masato; Özdemir, Şahin Kaya; , Nobuyuki (2003), "Experimentell extraktion av ett intrasslat fotonpar från två identiskt dekohererade par", Nature , 421 (6921): 343–346, Bibcode : 2003Natur.421..343Y , doi : 381ID , 10 : 351/81 , doi : 351/81 , 10 : 351 ID . 94 , S2CID 20824150 .
Pan, Jian-Wei; Gasparoni, Sara; Ursin, Rupert; Weihs, Gregor; Zeilinger, Anton (2003), "Experimentell entanglement purification of arbitrary unknown states", Nature , 423 ( 6938): 417–422, Bibcode : 2003Natur.423..417P , doi : 10.1038/nature01 , 41231 natur , 41231,3ID 41231 natur, 412331 , 61231 natur 93391 .
Pan, Jian-Wei; Simon, Christoph; Brunker, Časlav; Zeilinger , Anton (2001), " Entanglement purification for quantum communication", Nature , 410 ( 6832): 1067–1070, arXiv : quant-ph/0012026 , Bibcode : 2001Natur.410.1067P , doi .4 PM . 1323664 , S2CID 4424450 .
Nielsen, MA; Chuang, IL (2000), Quantum Computation and Quantum Information , Cambridge University Press, ISBN 0521635039
Bouwmeester, Dirk ; Ekert, Artur ; Zeilinger, Anton (2000), The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation , Springer, ISBN 3540667784
Newton, I. (1687), Principia Mathematica , vol. 1, Cambridge University Press
Luo, Zhicheng; Devetak, Igor (2007), "Effektivt implementerbara koder för quantumnyckelexpansion", Physical Review A , 75 (1): 010303, arXiv : quant-ph/0608029 , Bibcode : 2007PhRvA..75a0303L .A .5 , 101 .v . . . . . . . 10303 , S2CID 119491901
Mark M. Wilde, "From Classical to Quantum Shannon Theory", arXiv:1106.1445 .