Ladda qubit

Kretsschema för en laddnings-qubit-krets. Ön (prickad linje) bildas av den supraledande elektroden mellan gate-kondensatorn och junction-kapacitansen.

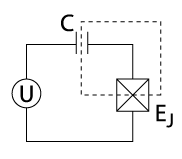
Inom quantum computing är en laddningsqubit (även känd som Cooper-pair box ) en qubit vars bastillstånd är laddningstillstånd ( dvs. tillstånd som representerar närvaron eller frånvaron av överskott av Cooper-par på ön). I supraledande kvantberäkning bildas en laddningsqubit av en liten supraledande ö kopplad av en Josephson-övergång (eller praktiskt taget supraledande tunnelövergång ) till en supraledande reservoar (se figur). Tillståndet för qubiten bestäms av antalet Cooper-par som har tunnlat över korsningen. I motsats till laddningstillståndet för en atomär eller molekylär jon, involverar laddningstillstånden för en sådan "ö" ett makroskopiskt antal ledningselektroner på ön. Kvantöverlagringen av laddningstillstånd kan uppnås genom att ställa in gate-spänningen U som styr den kemiska potentialen på ön. Laddningsqubiten läses vanligtvis ut genom att elektrostatiskt koppla ön till en extremt känslig elektrometer , såsom den radiofrekventa enkelelektrontransistorn .

Typiska T ₂ koherenstider för en laddningsqubit är i storleksordningen 1–2 μs. Nyligen arbete har visat att T ₂ gånger närmar sig 100 μs med en typ av laddningsqubit som kallas en transmon inuti en tredimensionell supraledande hålighet. Att förstå gränserna för T ₂ är ett aktivt forskningsområde inom supraledande kvantberäkningar .

Tillverkning

Charge qubits tillverkas med tekniker som liknar de som används för mikroelektronik . Enheterna är vanligtvis gjorda på kisel- eller safirskivor med hjälp av elektronstrålelitografi (till skillnad från fas-qubit , som använder fotolitografi ) och metalliska tunnfilmsförångningsprocesser. För att skapa Josephson-korsningar används vanligtvis en teknik som kallas skuggavdunstning ; detta innebär att källmetallen förångas växelvis i två vinklar genom den litografidefinierade masken i elektronstråleresisten. Detta resulterar i två överlappande lager av den supraledande metallen, mellan vilka ett tunt lager av isolator (normalt aluminiumoxid) avsätts.

Hamiltonian

Om Josephson-övergången har en korsningskapacitans $C_{\rm {J}}$ och gatekondensatorn $C_{\rm {g}}$ , då laddningsenergin (Coulomb) för ett Cooper-par är:

$E_{\rm {C}}=(2e)^{2}/2(C_{\rm {g}}+C_{\rm {J}}).$

Om $n$ anger antalet överflödiga Cooper-par på ön (dvs. dess nettoladdning är $-2ne$ ), då är Hamiltonian:

$H=\summa _{n}{\big [}E_{\rm {C}} (n-n_{\rm {g}})^{2}|n\rangle \langle n|-{\frac {1}{2}}E_{\rm {J}}(|n\rangle \langle n+1|+|n+1\rangle \langle n|){\big ]},$

där ${\displaystyle n_{\rm {g}}=C_{\rm {g}}V_{\rm {g}}/(2e)} är en$ kontrollparameter känd som effektiv offsetladdning ( $V_{\rm {g}}$ är gate-spänningen), och $\displaystyle E_{\rm {J}}}$ Josephson-energin för tunnelövergången.

Vid låg temperatur och låg grindspänning kan man begränsa analysen till endast de lägsta $n=0$ och $n=1$ tillstånden, och därför erhålla ett tvånivås kvantsystem (aka qubit ).

Observera att vissa nya artiklar använder en annan notation och definierar laddningsenergin som den för en elektron:

${\displaystyle E_{\rm {C}}=e^{2}/2(C_{\rm {g}}+C_{\rm$

och då är motsvarande Hamiltonian:

$H=\sum _{n}{\big [}4E_{\rm {C}}(n-n_{\rm {g}})^{2}|n\rangle \langle n|-{ \frac {1}{2}}E_{\rm {J}}(|n\rangle \langle n+1|+|n+1\rangle \langle n|){\big ]}.$

Fördelar

Hittills är realiseringarna av qubits som har haft störst framgång jonfällor och NMR , där Shors algoritm till och med har implementerats med NMR. Det är dock svårt att se dessa två metoder skalas till de hundratals, tusentals eller miljoner qubits som krävs för att skapa en kvantdator . Solid state- representationer av qubits är mycket lättare att skala, men de har själva sitt eget problem: dekoherens . Supraledare har dock fördelen att de är lättare att skala, och de är mer sammanhängande än normala solid-state-system.

Experimentella fortskrider

Implementeringen av supraledande laddningsqubits har gått snabbt sedan 1996. Design beskrevs teoretiskt 1997 av Shnirman, medan bevisen på kvantkoherens av laddningen i en Cooper-parbox publicerades i februari 1997 av Vincent Bouchiat et al . 1999 observerades koherenta svängningar i laddningen Qubit först av Nakamura et al. Manipulation av kvanttillstånden och full realisering av laddningsqubiten observerades 2 år senare. 2007 utvecklades en mer avancerad enhet känd som Transmon som visar förbättrade koherenstider på grund av dess minskade känslighet för laddningsbrus vid Yale University av Robert J. Schoelkopf, Michel Devoret , Steven M. Girvin och deras kollegor.