Energifrisättningshastighet (frakturmekanik)

Inom sprickmekanik är energifrisättningshastigheten , $G$ , den hastighet med vilken energi omvandlas när ett material genomgår brott . Matematiskt uttrycks energifrisättningshastigheten som minskningen av den totala potentiella energin per ökning av sprickytan, och uttrycks således i termer av energi per ytenhet. Olika energibalanser kan konstrueras som relaterar den energi som frigörs under brott till energin från den resulterande nya ytan, såväl som andra avledningsprocesser såsom plasticitet och värmealstring. Energifrisättningshastigheten är central inom området brottmekanik när man löser problem och uppskattar materialegenskaper relaterade till brott och utmattning .

Definition

Plot av belastning vs. förskjutning

Energifrisättningshastigheten $G$ definieras som den momentana förlusten av total potentiell energi $\Pi$ per enhet spricktillväxtarea $s$ ,

$G\equiv -{\frac {\partial \Pi }{\partial s}},$

där den totala potentiella energin skrivs i termer av den totala töjningsenergin $\Omega$ , ytdragkraft $\mathbf {t}$ , förskjutning $\mathbf {u}$ och kroppskraft $\mathbf {b}$ av

$\Pi =\Omega -\left\{\int _{{\mathcal {S}}_{t}}\mathbf {t} \cdot \mathbf {u} \,dS+\int _{\mathcal {V}}\mathbf {b} \cdot \mathbf {u} \,dV\right\}.$

Den första integralen är över ytan $S_{t}$ av materialet, och den andra över dess volym $V$ .

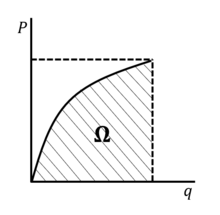
Figuren till höger visar plotten av en extern kraft $P$ vs. lastpunktsförskjutningen $q$ , där arean under kurvan är töjningsenergin. Det vita området mellan kurvan och $P$ -axeln kallas den komplementära energin. I fallet med ett linjärt-elastiskt material är $P(q)$ en rak linje och töjningsenergin är lika med den komplementära energin.

Föreskriven förskjutning

Vid föreskriven förskjutning kan töjningsenergin uttryckas i termer av den specificerade förskjutningen och sprickytan $\Omega (q,s)$ , ​​och förändringen i denna töjningsenergi är endast påverkas av förändringen i sprickytan: $\delta \Omega =(\partial \Omega /\partial s)\delta s$ . På motsvarande sätt uttrycks energifrisättningshastigheten i detta fall som

$G=-\left.{\frac {\partial \Omega }{\partial s}}\right|_{q}.$

Här kan man noggrant referera till $G$ som töjningsenergins frigöringshastighet.

Föreskrivna belastningar

När belastningen föreskrivs istället för förskjutningen, behöver töjningsenergin modifieras som $\Omega (q(P,s),s)$ . Energifrisättningshastigheten beräknas sedan som

$G=-\left.{\frac {\partial }{\partial s}}\right|_{P}\left(\Omega -Pq\right).$

Om materialet är linjärelastiskt så är $\Omega =Pq/2$ och man kan istället skriva

$G=\left.{\frac {\partial \Omega }{\partial s}}\right|_{P}.$

G i tvådimensionella fall

I fall av tvådimensionella problem är förändringen i spricktillväxtarean helt enkelt förändringen i spricklängd gånger provets tjocklek. Nämligen, $\partial s=B\partial a$ . Därför kan ekvationen för att beräkna $G$ modifieras för 2D-fallet:

• Föreskriven förskjutning: $G=-\left.{\frac {1}{B}}{\frac {\partial \Omega }{\partial a}}\right|_{q}.$
• Föreskriven belastning: $G=-\left.{\frac {1}{B}}{\frac {\partial }{\partial a}}\right|_{P}\left(\Omega -Pq\right).$
• Föreskriven belastning, linjär elastisk: $G=\left.{\frac {1}{B}}{\frac {\partial \Omega }{\partial a}}\right|_{P}.$

Man kan hänvisa till exemplet beräkningar inbäddade i nästa avsnitt för ytterligare information. Ibland skrivs töjningsenergin med $U=\Omega /B$ , en energi-per-enhets tjocklek. Detta ger

• Föreskriven förskjutning: $G=-\left.{\frac {\partial U}{\partial a}}\right|_{q}.$
• Föreskriven belastning: $G=-\left.{\frac {\partial }{\partial a}}\right|_{P}\left(U-{\frac {Pq}{B}}\right).$
• Föreskriven belastning, linjär elastisk: $G=\left.{\frac {\partial U}{\partial a}}\right|_{P}.$

Relation till stressintensitetsfaktorer

Energifrisättningshastigheten är direkt relaterad till spänningsintensitetsfaktorn associerad med ett givet tvådimensionellt belastningsläge ( Mode-I, Mode-II eller Mode-III) när sprickan växer rakt fram. Detta är tillämpligt på sprickor under plan spänning , plan töjning och antiplanskjuvning .

För Mode-I är energifrigöringshastigheten $G$ -hastigheten relaterad till Mode-I-spänningsintensitetsfaktorn $K_{I}$ för ett linjärt-elastiskt material med

$G={\frac {K_{I}^{2}}{E'}},$

där $E'$ är relaterad till Youngs modul $E$ och Poissons förhållande $\nu$ beroende på om materialet är under planspänning eller planspänning:

$E'={\begin{cases}E,&\mathrm {plan~stress} ,\\\\{\dfrac {E}{1-\nu ^{2}}},&\mathrm {plane ~strain} .\end{cases}}$

För Mode-II skrivs energifrisättningshastigheten på liknande sätt som

$G={\frac {K_{II}^{2}}{E'}}.$

För Mode-III (antiplanskjuvning) är energifrigöringshastigheten nu en funktion av skjuvmodulen μ $\displaystyle \mu }$ ,

$G={\frac {K_{III}^{2}}{2\mu }}.$

För en godtycklig kombination av alla belastningslägen kan dessa linjära elastiska lösningar läggas över varandra som

$G={\frac {K_{I}^{2}}{E'}}+{\frac {K_{II}^{2}}{E'}}+{\frac {K_{III }^{2}}{2\mu }}.$

Alternativ representation av $G$ i termer av $K$
$G={\begin{cases}{\frac {(1-\nu )^{2}}{E}}(K_{I}^{2}+K_{II}^{2})+(1- \nu )K_{III}^{2}&{\text{plantöjning}}\\{\frac {1}{E}}(K_{I}^{2}+K_{II}^{2} )&{\text{plane stress}}\end{cases}}$ Vilket kan ses vara ekvivalent med den tidigare representationen genom förhållandet mellan Youngs modul och skjuvmodulen: $E=2G(1+\nu )$

Förhållande till brottseghet

Spricktillväxt initieras när energifrisättningshastigheten överstiger ett kritiskt värde ${\displaystyle G_{c}} ,$ som är en materialegenskap

$G\geq G_{c},$

relateras den kritiska energifrigöringshastigheten ${\displaystyle G_{c}} till Mode-I-$ brottsegheten ${\displaystyle K_{IC}} ,$ annan materialegenskap, med

$G_{c}={\frac {K_{IC}^{2}}{E'}}.$

Beräknar G

Det finns en mängd olika metoder tillgängliga för att beräkna energifrisättningshastigheten givet materialegenskaper, provets geometri och belastningsförhållanden. Vissa är beroende av att vissa kriterier är uppfyllda, som att materialet är helt elastiskt eller till och med linjärelastiskt, och/eller att sprickan måste växa rakt fram. Den enda metod som presenteras som fungerar godtyckligt är att använda den totala potentiella energin. Om två metoder båda är tillämpliga, bör de ge identiska energifrisättningshastigheter.

Total potentiell energi

Den enda metoden för att beräkna $G$ för godtyckliga förhållanden är att beräkna den totala potentiella energin och differentiera den med avseende på sprickytan. Detta görs vanligtvis av:

• beräkning av spänningsfältet till följd av belastningen,
• beräkna töjningsenergin i materialet som härrör från spänningsfältet,
• beräkna det arbete som utförs av de externa belastningarna,

allt vad gäller sprickytan.

Exempelberäkning av $G$ med den totala potentiella energin

Dubbel utkragande balk (DCB) prov under dragbelastning. Det här problemet är tvådimensionellt och har en fast belastning, så med $s=aB$ , $G=-{\frac {1}{B}}\left.{\frac {\partial }{\partial a}}\right|_{P}(\Omega -Pq).$ Eftersom materialet är linjärelastiskt, $\Omega =Pq/2$ och alltså $G={\frac {1}{B}}{\frac {\partial \Omega }{\partial a}}.$ Spänningarna i DCB beror på böjspänningarna i varje fribärande balk, $\sigma _{11}(x,y)=-{\frac {M(x)y }{I}}=-{\frac {12Pxy}{Bh^{3}}},$ där $B$ är längden in på sidan. Genom att använda $W=\sigma _{11}^{2}/2E$ , har man nu töjningsenergin $\Omega =\int _{V} W\,dV=2B\int _{-h/2}^{h/2}\int _{0}^{a}{\frac {1}{2E}}\left({\frac {12Pxy} {Bh^{3}}}\right)^{2}\,dx\,dy,$ där faktorn 2 utanför beror på att det finns 2 fribärande balkar. Lösning, $\Omega ={\frac {P^{2}}{B^{3}}}{\frac {4a^{3}}{Eh^ {3}}},$ ta sedan en derivata med avseende på $a$ och dividera med $B$ , $G={\frac {P^{2}}{B^{2}}}{\frac {12a^{2}}{Eh^{3}}}.$

Efterlevnadsmetod

Om materialet är linjärt elastiskt kan beräkningen av dess energifrisättningshastighet förenklas mycket. I det här fallet är kurvan för last vs. lastpunktsförskjutning linjär med en positiv lutning, och förskjutningen per enhet kraft som appliceras definieras som efterlevnaden, C {\ $C}$

$C={\frac {q}{P}}.$

Motsvarande töjningsenergi $\Omega$ (area under kurvan) är lika med

$\Omega ={\frac {1}{2}}Pq={\frac {1}{2}}{\frac {q^{2}}{C}}={\frac {1}{ 2}}P^{2}C.$

Med hjälp av överensstämmelsemetoden kan man visa att energiutsläppshastigheten för båda fallen av föreskriven belastning och förskjutning blir

$G={\frac {1}{2}}P^{2}{\frac {\partial C}{\partial s}}.$

Exempelberäkning av $G$ med efterlevnadsmetoden

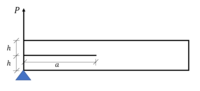
Ett dubbelt fribärande balkprov med tjocklek B (visas inte) Betrakta ett exemplar med dubbel fribärande balk (DCB) som visas i den högra bilden. Förskjutningen av en enda stråle är $\nu _{max}={\frac {Pa^{3}}{3EI}},\quad {\text{med}}\quad I={\frac {Bh^{3}}{12 }}.$ Den resulterande lastpunktsförskjutningen $q$ är därför $2\nu _{max}$ . Ersätt i ekvationen för efterlevnad och förenkla: $C={\frac {q}{P}}={\frac {8a^{3}}{EBh^{3}}}.$ Nu beräknas ${\displaystyle {\partial C}/{\partial s}} som$ ${\frac {\partial C}{\partial s}}={\frac {\partial C}{\partial a}}{\frac {\partial a}{\partial s}}=\left( {\frac {24a^{2}}{EBh^{3}}}\right)\left({\frac {1}{B}}\right).$ Slutligen kan energifrisättningshastigheten för detta DCB-prov uttryckas som $G(P,a)={\frac {1}{2}}P^{2}{\frac {\partial C}{\partial s}}={\frac {P^{2}} {B^{2}}}{\frac {12a^{2}}{Eh^{3}}}.$ Observera att energifrisättningshastigheten alternativt kan uttryckas i termer av $q$ och $a$ : $G(q,a)={\frac {3}{16}}{\frac {Eh^{3}q^{2 }}{a^{4}}},$ vilket indikerar att $G$ minskar med spricklängden $a$ för fallet med fast förskjutning och vice versa för fallet med fast belastning.

Flera provmetoder för icke-linjära material

Grafisk illustration av G under förhållanden med fast förskjutning och fast belastning

I fallet med föreskriven förskjutning, om spricklängden hålls fixerad, kan energifrisättningshastigheten beräknas med

$G=-\int _{0}^{q}{\frac {\partial P}{\partial s}}\,dq,$

medan vid föreskriven belastning,

$G=\int _{0}^{P}{\frac {\partial q}{\partial s}}\,dP.$

Som man kan se att, i båda fallen, returnerar energifrisättningshastigheten $G$ gånger förändringen i ytan $ds$ arean mellan kurvorna, vilket indikerar energin som förbrukas för den nya ytan som illustreras i den högra figuren

$Gds=-ds\int _{0}^{q}{\frac {\partial P}{\partial s}}\,dq=ds\int _{0}^{P}{\frac { \partial q}{\partial s}}\,dP.$

Sprickförslutning integrerad

Eftersom energifrisättningshastigheten definieras som den negativa derivatan av den totala potentiella energin med avseende på sprickyttillväxt, kan energifrisättningshastigheten skrivas som skillnaden mellan den potentiella energin före och efter att sprickan växer. Efter lite noggrann härledning leder detta till sprickstängningsintegralen

$G=\lim _{\Delta s\to 0}-{\ frac {1}{\Delta s}}\int _{\Delta s}{\frac {1}{2}}\,t_{i}^{0}\left(\Delta u_{i}^{+ }-\Delta u_{i}^{-}\right)\,dS,$

där $\Delta s$ är den nya sprickytan, $t_{i}^{0}$ är komponenterna i dragkraften som frigörs på den övre sprickytan när sprickan växer, ${\displaystyle \Delta u_{i}^{+}-\Delta u_{i}^{-}} är$ komponenterna i spricköppningsförskjutningen (skillnaden i förskjutningssteg mellan toppen och bottensprickytor), och integralen är över ytan av materialet $S$ .

Sprickförslutningsintegralen gäller endast för elastiska material, men är fortfarande giltig för sprickor som växer åt alla håll. Icke desto mindre, för en tvådimensionell spricka som verkligen växer rakt fram, förenklar sprickstängningsintegralen att

$G=\lim _{\Delta a\to 0 }{\frac {1}{\Delta a}}\int _{0}^{\Delta a}\sigma _{i2}(x_{1},0)u_{i}(\Delta a-x_{ 1},\pi )\,dx_{1},$

där $\Delta a$ är den nya spricklängden, och förskjutningskomponenterna skrivs som en funktion av de polära koordinaterna $r=\Delta a-x_{1}$ och $\theta =\pi$ .

Exempelberäkning av $G$ med användning av sprickförslutningsintegralen

Dubbel utkragande balk (DCB) prov under dragbelastning. Tänk på sprickan i DCB-provet som visas i figuren. Spännings- och förskjutningskomponenterna som inte är noll ges av as $\sigma _{22}(x_{1},0)={\frac {K_{I}}{\sqrt {2\pi x_{1}}}},\qquad u_{22}(\ Delta a-x_{1},\pi )={\frac {8K_{I}}{E}}{\sqrt {\frac {\Delta a_{1}-x_{1}}{2\pi }} }.$ Sprickförslutningen som är integrerad i detta linjärt-elastiska material, förutsatt att sprickan växer rakt fram, är $G={\frac {2K_{I}^{2}}{\pi E}}\,\lim _{\Delta a\to 0}{\frac {1}{\Delta a}}\ int _{0}^{\Delta a}{\sqrt {\frac {\Delta a_{1}-x_{1}}{x_{1}}}}\,dx_{1}.$ Överväg att skala om integralen med $\xi =x_{1}/\Delta a$ för $G={\frac {2K_{I}^{2}}{\pi E}}\int _{0}^{1 }{\sqrt {\frac {1-\xi }{\xi }}}\,d\xi ,$ där man beräknar den enklare integralen som ska vara $\int _{0}^{1}{\sqrt {\frac {1-\xi }{\xi }}}\,d\xi ={ \frac {\pi }{2}},$ lämnar energifrisättningshastigheten som $G={\frac {K_{I}^{2}}{E}},$ det förväntade förhållandet. I det här fallet är det inte enkelt att få $K_{I}$ direkt från problemets belastning och geometri, men eftersom sprickan växer rakt fram och materialet är linjärelastiskt, bör energifrisättningshastigheten här vara densamma som energifrisättningshastigheten beräknad med de andra metoderna. Detta gör att man indirekt kan hämta stressintensitetsfaktorn för detta problem som $K_{I}={\frac {P}{B}}{\frac {2a}{h}}{\sqrt {\frac {3}{h}}}.$

J - integral

I vissa situationer kan energifrisättningshastigheten $G$ beräknas med J-integralen , dvs. $G=J$ , med hjälp av

$J=\int _{\Gamma }\left(Wn_{1}-t_{i}\,{\frac {\partial u_{i}}{\partial x_{1}}}\right)\,d\Gamma ,$

där $W$ är den elastiska töjningsenergitätheten, $n_{1}$ är $x_{1}$ -komponenten av enhetsvektorn normal till $\Gamma$ , kurvan som används för linjeintegralen, $t_{i}$ är komponenterna i dragvektorn $\mathbf {t} ={\boldsymbol {\sigma }}\cdot \mathbf {n}$ , där ${\boldsymbol {\sigma }}$ är spänningstensorn, och $u_{i}$ är komponenterna i förskjutningsvektorn.

Denna integral är noll över en enkel stängd bana och är banoberoende , vilket gör att vilken enkel bana som helst som börjar och slutar på sprickytorna kan användas för att beräkna $J$ . För att likställa energifrigöringshastigheten med J-integralen, $G=J$ , måste följande villkor vara uppfyllda:

• sprickan måste växa rakt fram, och
• deformationen nära sprickan (omsluten av $\Gamma$ ) måste vara elastisk (ej plastisk).

J-integralen kan beräknas med dessa villkor överträdda, men då $G\neq J$ . När de inte bryts kan man relatera energifrigöringshastigheten och J-integralen till elasticitetsmodulerna och spänningsintensitetsfaktorerna med hjälp av

$G=J={\frac {K_{I}^{2}}{E'}}+{\frac {K_{II}^{2}}{E'}}+{\frac {K_ {III}^{2}}{2\mu }}.$

Exempel på beräkning av $G$ med J-integralen

Dubbel utkragande balk (DCB) prov under dragbelastning. J-integralbana för DCB-provet under dragbelastning. Betrakta det dubbla fribärande balkexemplaret som visas i figuren, där sprickan centrerad i strålen med höjden $2h$ har en längd av $a$ och en belastning $P$ appliceras på öppna sprickan. Antag att materialet är linjärt-elastiskt och att sprickan växer rakt fram. Betrakta en rektangulär bana som visas i den andra figuren: börja på den övre sprickan, (1) gå upp till toppen vid ${\displaystyle h} ,$ (2) gå till höger förbi sprickans spets, (3) gå ner till botten vid $-2h$ , (4) gå längst ned till vänster och (5) gå tillbaka upp till den nedre sprickytan. J-integralen är noll längs många delar av denna väg. Materialet avlastas effektivt bakom sprickan, så både töjningsenergitätheten och dragkraften är noll längs (1) och (5), och därmed J-integralen. Längs (2) och (4) har man $n_{1}=0$ samt $\mathbf {t} =\mathbf {0}$ (ingen dragkraft på den fria ytan ), så J-integralen är också noll på (2) och (4). Detta lämnar endast (3); om man antar att en är tillräckligt långt från sprickan på (3), är dragtermen noll eftersom $u_{1}=0$ och $\sigma _{12}=0$ långt ifrån sprickan, lämnar $J=\int _{\Gamma _{3}}Wn_{1}\,d\Gamma _{3}.$ $n_{1}=1$ längs (3), och $W$ beror på böjspänning för en fribärande balk $\sigma _{11}(y)=-{\frac {My}{I}}=-{\frac { 12Pay}{Bh^{3}}},$ där $B$ är längden in på sidan. Genom att använda $W=\sigma _{11}^{2}/2E$ har man nu $J=2\int _{-h/2}^{h/2}{\ frac {1}{2E}}\left({\frac {12Pay}{Bh^{3}}}\right)^{2}\,dy,$ där faktorn 2 utanför beror på att det finns 2 fribärande balkar. Lösning, $G=J={\frac {P^{2}}{B^{2}}}{\frac {12a^{2}}{Eh^{3}}}.$

Beräkningsmetoder inom sprickmekanik

Det finns en handfull metoder för att beräkna $G$ med finita element. Även om en direkt beräkning av J-integralen är möjlig (med användning av töjningar och spänningar som matas ut av FEA ), finns det ungefärliga tillvägagångssätt för någon typ av spricktillväxt och ger rimlig noggrannhet med enkla beräkningar. Detta avsnitt kommer att utveckla några relativt enkla metoder för sprickanalys med numeriska simuleringar.

Nodal frisättningsmetod

Om sprickan växer rakt kan energifrisättningshastigheten sönderdelas som en summa av 3 termer $G_{i}$ associerade med energin i varje 3 lägen. Som ett resultat kan Nodal Release-metoden (NR $G_{i}$ användas för att bestämma från FEA-resultat. Energifrisättningshastigheten beräknas vid noderna för det finita elementnätet för sprickan vid en initial längd och förlängs med ett litet avstånd $\Delta a$ . Först beräknar vi förskjutningsvariationen vid noden av intresse $\Delta {\vec {u}}={\vec {u}}^ {(t+1)}-{\vec {u}}^{(t)}$ (före och efter att sprickspetsnoden släpps). För det andra håller vi reda på nodkraften ${\vec {F}}$ som matas ut av FEA. Slutligen kan vi hitta alla komponenter i $G$ med hjälp av följande formler:

Figur 1: Sprickavveckling mellan två på varandra följande tidssteg med nodalfrigöring (NR)

$$G_{1}^{\text{NR}}={\frac {1}{\Delta a}}F_{2}{\frac {\ Delta u_{2}}{2}}$$

$$G_{2}^{\text{NR}}={\frac {1}{\Delta a}}F_{1}{\frac {\ Delta u_{1}}{2}}$$

$$G_{3}^{\text{NR}}={\frac {1}{\Delta a}}F_{3}{\frac {\ Delta u_{3}}{2}}$$

Där $\Delta a$ är bredden på elementet som avgränsar sprickspetsen. Metodens noggrannhet beror i hög grad på maskens förfining, både eftersom förskjutningen och krafterna beror på den, och eftersom $G=\lim _{\Delta a\to 0}G^ {\text{NR}}$ . Observera att ekvationerna ovan härleds med användning av sprickförslutningsintegralen.

Om energifrisättningshastigheten överstiger ett kritiskt värde kommer sprickan att växa. I detta fall utförs en ny FEA-simulering (för nästa tidssteg) där noden vid sprickspetsen släpps. För ett avgränsat substrat kan vi helt enkelt sluta upprätthålla fasta Dirichlet-gränsvillkor vid sprickspetsnoden i föregående tidssteg (dvs. förskjutningar är inte längre begränsade). För en symmetrisk spricka skulle vi behöva uppdatera domänens geometri med en längre spricköppning (och därför generera ett nytt nät).

Modifierad sprickförslutning integral

I likhet med nodalfrisättningsmetoden är MCCI (Modified Crack Closure Integral) en metod för att beräkna energifrisättningshastigheten med användning av FEA -nodförskjutningar $(u_{i}^{j})$ och krafter $(F_{i}^{j})$ . Där $i$ representerar riktningen som motsvarar de kartesiska basvektorerna med ursprung vid sprickspetsen, och $j$ representerar nodalindexet. MCCI är mer beräkningseffektiv än nodalfrisättningsmetoden eftersom den bara kräver en analys för varje steg av spricktillväxt.

Ett nödvändigt villkor för MCCI-metoden är enhetlig elementlängd $(\Delta a)$ längs sprickytan i riktningen ${\displaystyle x_{1}-} .$ Dessutom kräver denna metod tillräcklig diskretisering så att spänningsfält över längden av ett element är självlika . Detta innebär att $K(a+\Delta a)\approx K(a)$ när sprickan fortplantar sig. Nedan finns exempel på MCCI-metoden med två typer av vanliga finita element.

4-nodselement

Figur 2: Schematisk över MCCI-processen för linjära rektangulära element med 4 noder.

De fyrkantiga linjära elementen med fyra noder som visas i figur 2 har ett avstånd mellan noderna $j$ och $j+1$ lika med $\Delta a.$ Betrakta en spricka med dess spets placerad vid nod $j.$ I likhet med nodalfrigöringsmetoden, om sprickan skulle fortplanta sig en elementlängd längs symmetrilinjen (parallellt med x $\displaystyle x_{1}}$ -axeln) skulle spricköppningsförskjutningen vara förskjutningen vid föregående sprickspets, dvs ${\boldsymbol {u^{j}}}$ och kraften vid den nya sprickspetsen ( $\displaystyle (j+1)}$ skulle vara ${\boldsymbol {F}}^{j+1}.$ Eftersom spricktillväxten antas vara självlik är förskjutningen vid nod $j$ efter att sprickan har fortplantat sig lika med förskjutningen vid nod $j-1$ innan sprickan fortplantar sig. Samma koncept kan appliceras på krafterna vid nod $j+1$ och $j.$ Genom att använda samma metod som visas i nodfrisättningssektionen återställer vi följande ekvationer för energifrisättningshastighet:

$G_{1}^{\text{MCCI}}={\frac {1}{2\Delta a}}F_{2} ^{j}{\Delta u_{2}^{j-1}}$

$G_{2}^{\text{MCCI}}={\frac {1}{2\Delta a}}F_{1} ^{j}{\Delta u_{1}^{j-1}}$

$G_{3}^{\text{MCCI}}={\frac {1}{2\Delta a}}F_{3} ^{j}{\Delta u_{3}^{j-1}}$

Där $\Delta u_{i}^{j-1}=u_{i}^{(+) j-1}-u_{i}^{(-)j-1}$ (förskjutning över respektive under sprickytan). Eftersom vi har en symmetrilinje parallell med sprickan kan vi anta $u_{i}^{(+)j-1}=-u_{i}^{(-)j-1}.$

Således, $\Delta u_{i}^{j-1}=2u_{i}^{(+)j-1}.$

8-nodselement

Figur 3: Schematisk över MCCI-processen för kvadratiska rektangulära element med 9 noder.

De rektangulära elementen med 8 noder som visas i figur 3 har kvadratiska basfunktioner . Processen för att beräkna G är densamma som 4-nodselementen med undantaget att $\Delta a$ (spricktillväxten över ett element) nu är avståndet från nod $j$ till $j+2.$ Återigen, med antagandet om en självliknande tillväxt av raka sprickor, kan energifrisättningshastigheten beräknas med hjälp av följande ekvationer:

$G_{1}^{\text{MCCI}}={\frac {1}{2\Delta a}}\left(F_{2}^{j}{\Delta u_{2}^{j-2}}+F_{2}^{j+1}{\Delta u_ {2}^{j-1}}\höger)$

$G_{2}^{\text{MCCI}}={\frac {1}{2\Delta a}}\left(F_{1}^{j}{\Delta u_{1}^{j-2}}+F_{1}^{j+1}{\Delta u_ {1}^{j-1}}\right)$

$G_{3}^{\text{MCCI}}={\frac {1}{2\Delta a}}\left(F_{3}^{j}{\Delta u_{3}^{j-2}}+F_{3}^{j+1}{\Delta u_ {3}^{j-1}}\höger)$

Precis som med nodalfrisättningsmetoden är noggrannheten hos MCCI starkt beroende av diskretiseringsnivån längs sprickspetsen, dvs $G=\lim _{\Delta a\to 0}G^{\text{MCCI}}.$ Noggrannheten beror också på val av element. Ett nät av kvadratiska element med 8 noder kan ge mer exakta resultat än ett nät av linjära element med 4 noder med samma antal frihetsgrader i nätet.

Domänintegral metod för J

Figur 4: Konturdomänintegral för J-integralen

J-integralen kan beräknas direkt med användning av finita elementnät- och formfunktioner. Vi betraktar en domänkontur som visas i figur 4 och väljer en godtycklig jämn funktion ${\displaystyle {\tilde {q}} (x_{1},x_{2})=\summa _{i}N_{i}(x_{1},x_{2}){\tilde {q}}_{i}} så$ att ${\tilde {q}}=1$ på $\Gamma$ och ${\tilde {q}}=0$ på ${\mathcal {C }}_{1}$ .

För linjära elastiska sprickor som växer rakt fram, $G=J$ . Energifrisättningshastigheten kan sedan beräknas över området som begränsas av konturen med en uppdaterad formulering: $J= \int _{\mathcal {A}}(\sigma _{ij}u_{i,1}{\tilde {q}}_{,j}-W{\tilde {q}}_{,1}) d{\mathcal {A}}$

Formeln ovan kan tillämpas på valfritt ringformigt område som omger sprickspetsen (i synnerhet kan en uppsättning angränsande element användas). Denna metod är mycket exakt, även med ett grovt nät runt sprickspetsen (man kan välja en integrationsdomän som ligger långt bort, med spänningar och förskjutning mindre känsliga för nätförfining)

Härledning av J-integralen för domänintegralmetoden

J-integralen kan uttryckas över hela konturen enligt följande: $G=J=\int _{\Gamma }(Wn_{1}-t_{i}{\frac {\partial u_{i}}{\partial x_{1}}}) d\Gamma =\int _{{\mathcal {C}}_{1}+{\mathcal {C}}_{+}+{\mathcal {C}}_{-}-{\mathcal {C} }}(Wn_{1}-\sigma _{ij}n_{j}{\frac {\partial u_{i}}{\partial x_{1}}}){\tilde {q}}d\Gamma$ Med ${\mathcal {C}}={\mathcal {C}}_{1}+{\mathcal {C}}_{+}+{\ matematisk {C}}_{-}-\Gamma$ . ${\vec {n}}=-{\vec {m}}$ , ${\tilde {q}}=0$ på ${ \mathcal {C}}_{1}$ och arbetet och spänningarna tar ut på ${\mathcal {C}}_{+}$ och ${\displaystyle {\mathcal {C}}_ {-}} , därför$ leder detta genom tillämpning av divergenssatsen till : $J=\int _{\mathcal {C}}(-Wm_{1}+\sigma _{ij}m_{i}{\frac {\partial u_{i}}{\partial x_{ 1}}})d{\mathcal {C}}=\int _{\mathcal {A}}({\frac {\partial \sigma _{ij}u_{i,1}{\tilde {q}} }{\partial x_{j}}}-{\frac {\partial W{\tilde {q}}}{\partial x_{1}}})d{\mathcal {A}}$ Slutligen, genom att notera att ${\frac {\partial W}{\partial x_{1}}}=\sigma _{ij }{\frac {\partial ^{2}u_{i}}{\partial x_{j}\partial x_{1}}}$ och med hjälp av jämviktsekvationen: $J=\int _{\mathcal {A}}(\sigma _{ij}u_{i ,1}{\tilde {q}}_{,j}-W{\tilde {q}}_{,1})d{\mathcal {A}}$

2-D sprickspets singulära element

De ovan nämnda metoderna för att beräkna energifrisättningshastigheten närmar sig asymptotiskt den faktiska lösningen med ökad diskretisering, men lyckas inte helt fånga sprickspetsens singularitet. Mer exakta simuleringar kan göras genom att använda kvartspunktselement runt sprickspetsen. Dessa element har en inbyggd singularitet som mer exakt producerar spänningsfält runt sprickspetsen. Fördelen med kvartspunktsmetoden är att den tillåter grövre finita elementmaskor och avsevärt minskar beräkningskostnaden. Dessutom är dessa element härledda från små modifieringar av vanliga finita element utan att kräva speciella beräkningsprogram för analys. För detta avsnitt kommer elastiska material att undersökas, även om denna metod kan utvidgas till elastisk- plastisk brottmekanik. Om man antar perfekt elasticitet kommer spänningsfälten att uppleva en ${\frac {1}{\sqrt {r}}}$ sprickspets singularitet.

8-nods isoparametriskt element

Figur 5: Kartlagt och överordnat element för det isoparametriska finita elementet med 8 noder. Notera kvartspunktsplatsen för noderna i det mappade elementet.

Det kvadratiska elementet med 8 noder beskrivs i figur 5 i båda föräldrarymden med lokala koordinater $\xi$ och $\eta ,$ och av det mappade elementet i fysiskt/globalt utrymme med $x$ och $y.$ Det överordnade elementet mappas från det lokala rummet till det fysiska rummet av formfunktionerna $N_{i}(\xi ,\eta )$ och graden av frihet koordinater $(x_{i},y_{i}).$ Sprickspetsen är placerad vid $\xi =-1,\eta =-1$ eller $x=0,y=0.$

$x(\xi ,\eta )=\summa _{i=1}^{8}N_{i}( \xi ,\eta )x_{i}$

$y(\xi ,\eta )=\summa _{i= 1}^{8}N_{i}(\xi ,\eta )y_{i}$

På liknande sätt kan förskjutningar (definierade som ${\displaystyle u\equiv u_{1},v\equiv u_{2}} )$ också kartläggas.

$u(\xi ,\eta )=\summa _{i=1}^{8}N_{i}( \xi ,\eta )u_{i}$

$v(\xi ,\eta )=\summa _{i= 1}^{8}N_{i}(\xi ,\eta )v_{i}$

En egenskap för formfunktioner i den finita elementmetoden är kompakt stöd , specifikt Kronecker delta -egenskapen (dvs. $N_{i}=1$ vid nod $i$ och noll vid alla andra noder) . Detta resulterar i följande formfunktioner för de 8-nods kvadratiska elementen:

$N_{1}={\frac {-(\xi -1)(\eta -1)(1+ \eta +\xi )}{4}}$

$N_{2}={\frac {(\xi +1)(\eta -1)(1+\eta -\xi )}{4}}$

$N_{3}={\frac {(\xi +1)(\eta +1)(-1+ \eta +\xi )}{4}}$

$N_{4}={\frac {-(\xi -1)(\eta +1)(- 1+\eta -\xi )}{4}}$

$N_{5}={\frac {(1-\xi ^{2})(1-\eta )}{2}}$

$N_{6}={\frac {(1+\xi )(1-\eta ^{2})}{2}}$

$N_{7}={\frac {(1-\xi ^{2})(1+\eta )}{2}}$

$N_{8}={\frac {(1-\xi )(1-\eta ^{2})}{2}}$

När man betraktar en linje framför sprickan som är linjär med $x$ - axeln (dvs. $N_{i}(\xi ,\eta = -1)$ ) alla basfunktioner är noll förutom $N_{1,2,5}.$

$N_{1}(\xi ,-1)=-{\frac {\xi (1-\xi)}{2}}$

$N_{2}(\xi ,-1)={\frac {\xi (1+\xi)}{2}}$

$N_{5}(\xi ,-1)=(1-\xi ^{2})$

Att beräkna den normala töjningen innebär att man använder kedjeregeln för att ta derivatan av förskjutning med avseende på $x.$

$\gamma _{xx}={\frac {\partial u}{\partial x }}=\summa _{i=1,2,5}{\frac {\partial N_{i}}{\partial \xi }}{\frac {\partial \xi }{\partial x}}u_{ i}$

Figur 6: Triangulärt element mappat från rektangulärt element med 8 noder.

Om noderna är jämnt fördelade på det rektangulära elementet kommer stammen inte att innehålla singulariteten. Genom att flytta noderna 5 och 8 position till en fjärdedel av längden $({\tfrac {L}{4}})$ av elementet närmare sprickspetsen som ses i figur 5, kan mappningen från $\xi \rightarrow x$ blir:

$x(\xi )={\frac {\xi (1+\xi)}{2}}L+( 1-\xi ^{2}){\frac {L}{4}}$

Att lösa för $\xi$ och ta derivatan resulterar i:

${\displaystyle \xi (x)=-1+2{\sqrt {\frac {x}{L}}}} ∂ ξ$

$displaystyle {\frac {\partial \xi }{\partial x}}={\frac {1}{\sqrt {xL}}}}$

Om detta resultat kopplas in i ekvationen för töjning erhålls det slutliga resultatet:

$\gamma _{xx}={\frac {4}{L}}\left( {\frac {u_{2}}{2}}-u_{5}\right)+{\frac {1}{\sqrt {xL}}}\left(2u_{5}-{\frac {u_{ 2}}{5}}\right)$

Genom att flytta mittnoderna till en kvartsposition resulterar det i korrekt ${\frac {1}{\sqrt {r}}}$ sprickspets singularitet.

Andra elementtyper

Figur 7: Naturligt triangelelement

Den rektangulära elementmetoden tillåter inte att singulära element lätt maskas runt sprickspetsen. Detta hindrar förmågan att fånga spänningsfältens vinkelberoende, vilket är avgörande för att bestämma sprickvägen. Förutom längs elementets kanter ${\frac {1}{\sqrt {r}}}$ singulariteten i ett mycket litet område nära sprickspetsen. Figur 6 visar en annan kvartspunktsmetod för att modellera denna singularitet. Det rektangulära elementet med 8 noder kan mappas till en triangel. Detta görs genom att kollapsa noderna på linjen $\xi =-1$ till mittnodsplatsen och flytta mellannoderna på $\eta =\pm 1$ till kvartspunktsplatsen. Den kollapsade rektangeln kan lättare omge sprickspetsen men kräver att elementets kanter är raka annars kommer noggrannheten i beräkningen av spänningsintensitetsfaktorn att minska.

En bättre kandidat för kvartspunktsmetoden är den naturliga triangeln som ses i figur 7. Elementets geometri gör att sprickspetsen lätt kan omges och maskningen förenklas. Efter samma procedur som beskrivs ovan är förskjutnings- och töjningsfältet för de triangulära elementen:

$u=u_{3}+{\sqrt {\ frac {x}{L}}}\left[4u_{6}-3u_{3}-u_{1}\right]+{\frac {x}{L}}\left[2u_{1}+2u_{ 3}-4u_{6}\höger]$

$\gamma _{xx}={\frac {\partial u}{\partial x}}={\frac {1}{\sqrt {xL}}}\left[-{\frac {u_{1}}{2}}-{\frac {3u_{3}}{2}}+2u_{6}\right]+{\frac {1}{L}}\left[2u_{1} +2u_{3}-4u_{6}\right]$

Denna metod återger de två första termerna i Williams-lösningarna med en konstant och singulär term.

En fördel med kvartspunktsmetoden är att den lätt kan generaliseras till 3-dimensionella modeller. Detta kan avsevärt minska beräkningen jämfört med andra 3-dimensionella metoder men kan leda till fel om den sprickspetsen fortplantar sig med en stor grad av krökning.

Se även

• Frakturmekanik
• Stressintensitetsfaktor
• Frakturseghet
• J-integral

externa länkar

• Icke-linjär frakturmekanik av prof. John Hutchinson (från Harvard University)
• Griffith's Strain Energy Release Rate på www.fracturemechanics.org